Содержание
- 2. 1.Числовые ряды. Определение. 2.Необходимый признак сходимости. 3.Достаточные признаки сходимости рядов с положительными членами. 4.Знакопеременные ряды. 5.Знакочередующиеся
- 3. Сумма ряда или ряд, — математическое выражение, позволяющее записать бесконечное количество слагаемых и подразумевающее значение их
- 4. Пусть дана бесконечная последовательность чисел: (1) Выражение: (2) называется числовым рядом, а числа - членами ряда.
- 5. Если последовательность частичных сумм имеет конечный предел (3) то этот предел называется суммой ряда. В этом
- 6. Необходимый признак сходимости ряда ● Если ряд сходится, то его общий член к нулю при стремится
- 7. Достаточные признаки сходимости рядов с положительными членами. 1) Признак сравнения рядов (5) (6) ● Если, начиная
- 8. 2) Признак Даламбера. ● Если существует предел то при ℓ ряд (5) сходится , о сходимости
- 9. Примеры 1. Написать пять первых членов ряда по данному общему члену (*) 2. Найти для ряда
- 10. Частичная сумма ряда Отсюда следует, что ряд (*) сходится и его сумма S=1 3. Написать формулу
- 11. Учитывая, что знаки членов ряда чередуются, получим если ,то расходится! => ряд расходится - расходиться! 4.
- 12. 5. Исследовать по признаку Даламбера сходимость ряда: ℓ=0 ряд сходится. 6. Исследовать по признаку Коши сходимость
- 13. Знакопеременные ряды Определение: Если члены числового ряда с разными знаками, то такой ряд будет называться знакопеременным.
- 14. ● Если же ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.
- 15. Знакочередующиеся ряды Ряд (3) (3`) где n>0 (n=1,2,3,…) называется знакочередующимся. Этот ряд является частным случаем знакопеременного
- 16. Признак Лейбница Если члены знакочередующегося ряда (3) убывают по абсолютной величине и 0 , то такой
- 17. Члены данного ряда убывают по абсолютной величине, знаки чередуются и предел =>ряд сходится Составлен ряд (а)
- 18. Итак: 1) Сходятся условно ряды с общим членом или 2) Абсолютно сходятся ряды с общим членом
- 20. Скачать презентацию

















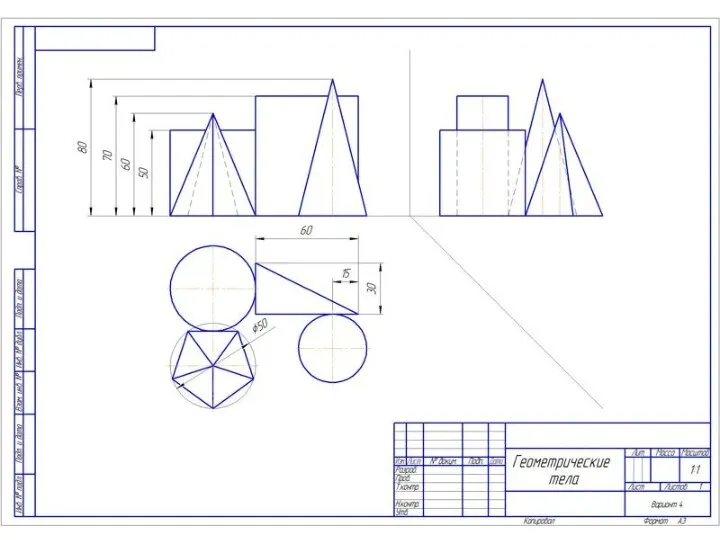 Геометрические тела. 9 класс
Геометрические тела. 9 класс Квадрат та його властивості
Квадрат та його властивості Игра путешествие В гостях у Незнайки
Игра путешествие В гостях у Незнайки Перпендикулярность плоскостей
Перпендикулярность плоскостей Дискретная математика
Дискретная математика Применение векторного и смешанного произведений векторов в решении геометрических задач
Применение векторного и смешанного произведений векторов в решении геометрических задач Системы неравенств
Системы неравенств Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Тайна Египетского треугольника
Тайна Египетского треугольника Сокращение дробей. 6 класс
Сокращение дробей. 6 класс Площадь круга
Площадь круга Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова
Урок математики 4 класс Тема: «Письменное умножение на числа, оканчивающиеся нулями» МБУО «Новообинцевская средняя общеобразова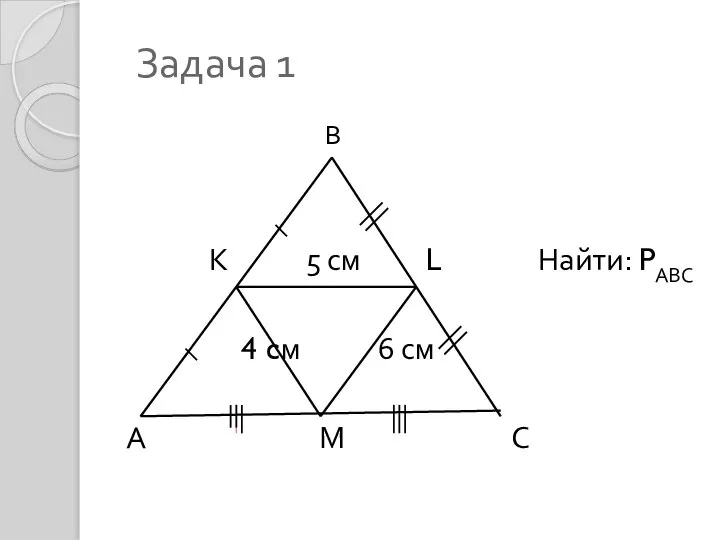 Средняя линия треугольника
Средняя линия треугольника Презентация на тему Параллельные прямые, треугольники
Презентация на тему Параллельные прямые, треугольники  Разные задачи на многогранники, цилиндр, конус и шар
Разные задачи на многогранники, цилиндр, конус и шар Решение задач. 3 класс
Решение задач. 3 класс Свойства функций
Свойства функций Fraktaly_Osnovnye_ponyatia (1)
Fraktaly_Osnovnye_ponyatia (1) Окружность и круг
Окружность и круг Преобразование выражений содержащих степень с отрицательным целым показателем
Преобразование выражений содержащих степень с отрицательным целым показателем Презентация на тему Математический диктант (4 класс)
Презентация на тему Математический диктант (4 класс)  Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения  Трапеция. Свойство углов равнобедренной трапеции
Трапеция. Свойство углов равнобедренной трапеции Вектор. Равенство векторов
Вектор. Равенство векторов Математические игры
Математические игры Правильные многогранники
Правильные многогранники Графическое решение уравнений
Графическое решение уравнений Симетричні фігури
Симетричні фігури