Содержание
- 2. Отношения Упорядоченные наборы Произведение множеств Бинарные отношения Представление отношений Функциональные отношения Отношения эквивалентности Отношения порядка Вопросы
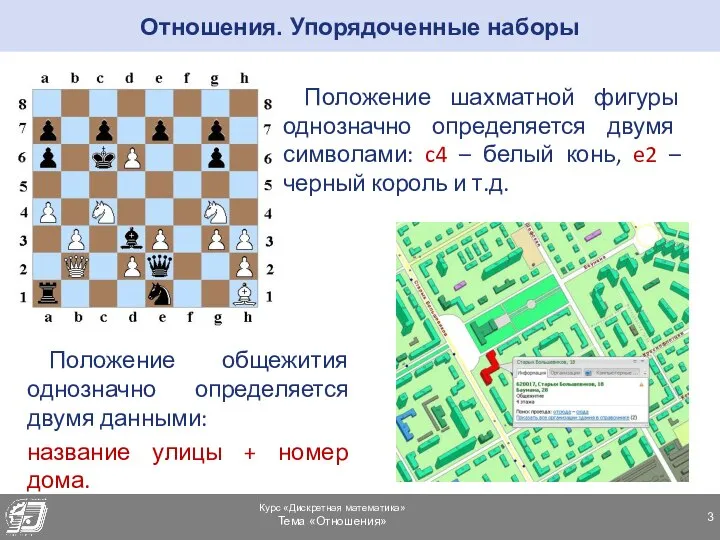
- 3. Отношения. Упорядоченные наборы Положение шахматной фигуры однозначно определяется двумя символами: c4 – белый конь, e2 –
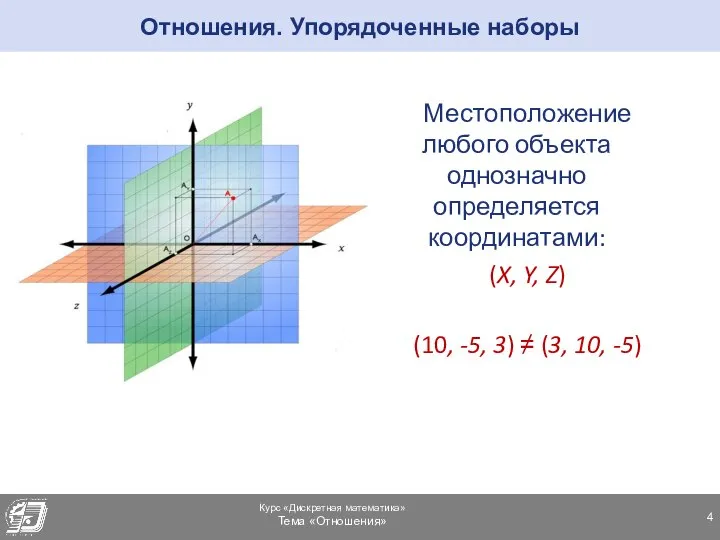
- 4. Отношения. Упорядоченные наборы Местоположение любого объекта однозначно определяется координатами: (X, Y, Z) (10, -5, 3) ≠
- 5. Отношения. Упорядоченные наборы Данные о человеке однозначно определяются: Фамилия Имя Отчество Дата рождения (чч.мм.гггг) Место рождения
- 6. Отношения. Упорядоченные наборы Упорядоченный набор (кортеж, n-ка) данных – последовательность из n объектов a1, a2,… ,
- 7. Отношения. Прямое произведение множеств Прямое произведение множеств A 1, A 2, … , A n есть
- 8. Отношения. Прямое произведение множеств Теорема: Для конечных множеств A и B |A×B|=|A|×|B|. Лемма: (A × B)
- 9. Бинарные отношения Бинарным отношением между множествами A и B называется подмножество R прямого произведения A ×
- 10. Бинарные отношения Пример: Семья Weasley. Отношение R = {(x, y)| x – отец y }. Тогда
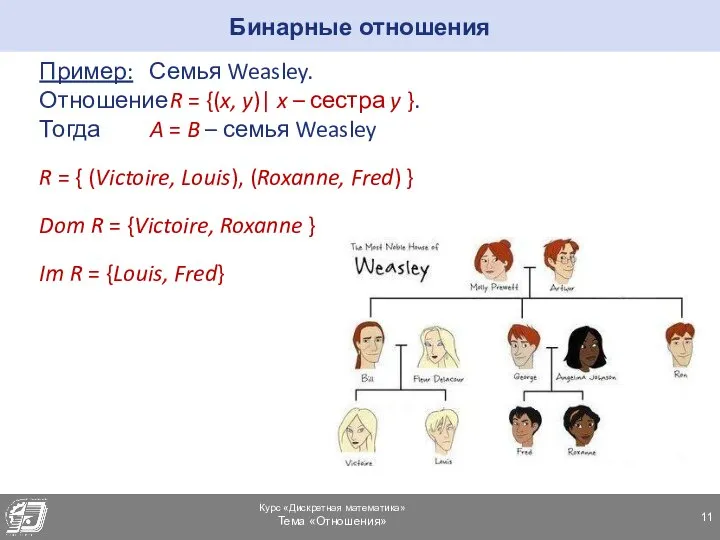
- 11. Бинарные отношения Пример: Семья Weasley. Отношение R = {(x, y)| x – сестра y }. Тогда
- 12. Бинарные отношения Особые виды отношений Пусть R - отношение между множествами A и B. Обратное отношение
- 13. Операции над отношениями Отношение – это некоторое множество ⟹ допустимы все теоретико-множественные операции Пример: ℕ -
- 14. Композиция отношений Пусть R1 : A → B и R2 : B → C. Композиция отношений
- 15. Бинарные отношения Свойства отношений Пусть R - отношение на множестве A. Рефлексивность ∀x ∈ A ⇒
- 16. Бинарные отношения Свойства отношений Теорема: Если R ⊂ A2 - отношение на множестве А, то R
- 17. Представление отношений прямым перечислением всех пар в виде графа графиком матрицей (машинное представление) Пусть R ⊂
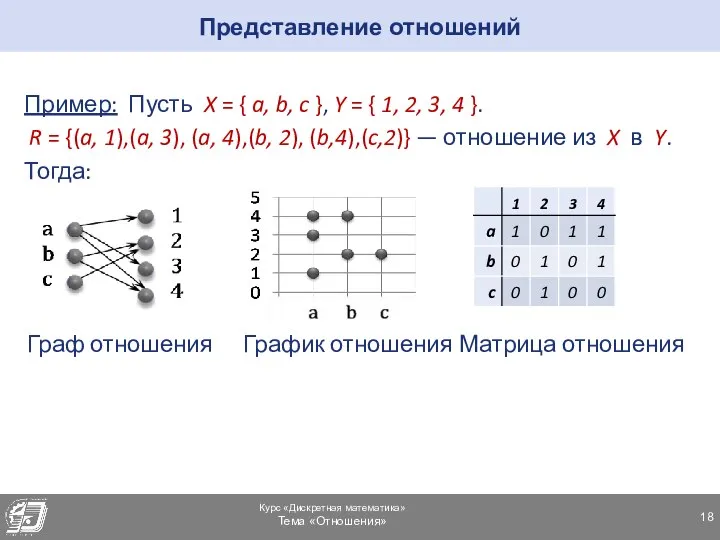
- 18. Представление отношений Пример: Пусть X = { a, b, c }, Y = { 1, 2,
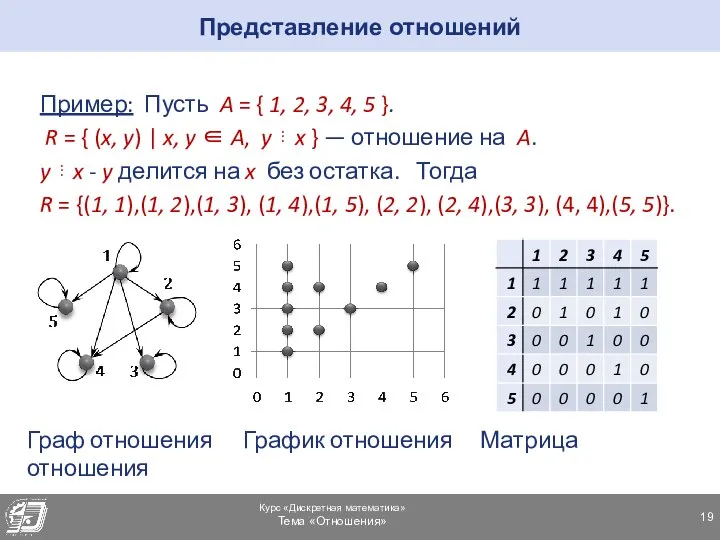
- 19. Представление отношений Пример: Пусть A = { 1, 2, 3, 4, 5 }. R = {
- 20. Пусть f - отношение между множествами A и B. Отношение называется функциональным (функцией), если ∀x ∈
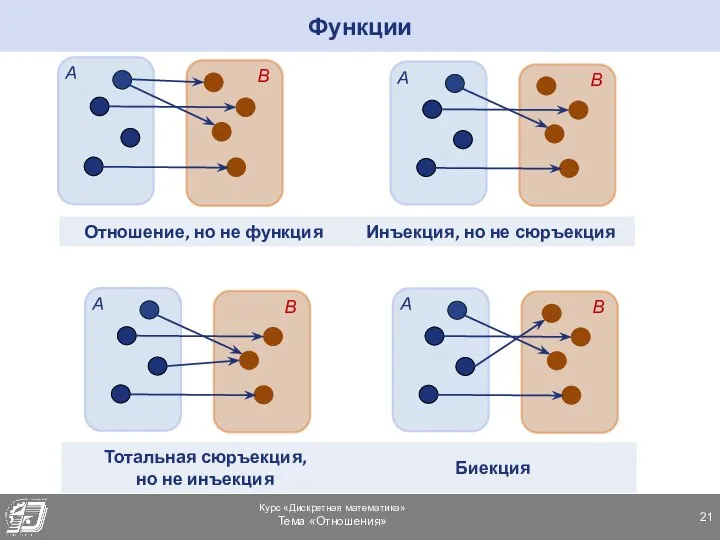
- 21. Функции
- 22. Теорема: Если f : A → B - тотальная биекция, то отношение f-1 ⊂ B ×
- 23. Композиция функций называется суперпозицией Обозначение: если f : A → B и g : B →
- 24. Отношения эквивалентности Отношение эквивалентности – рефлексивное, симметричное, транзитивное отношение. Если R - отношение эквивалентности, то говорят,
- 25. Отношения эквивалентности Теорема: отношение эквивалентности на некотором множестве A порождает его разбиение на классы эквивалентности –
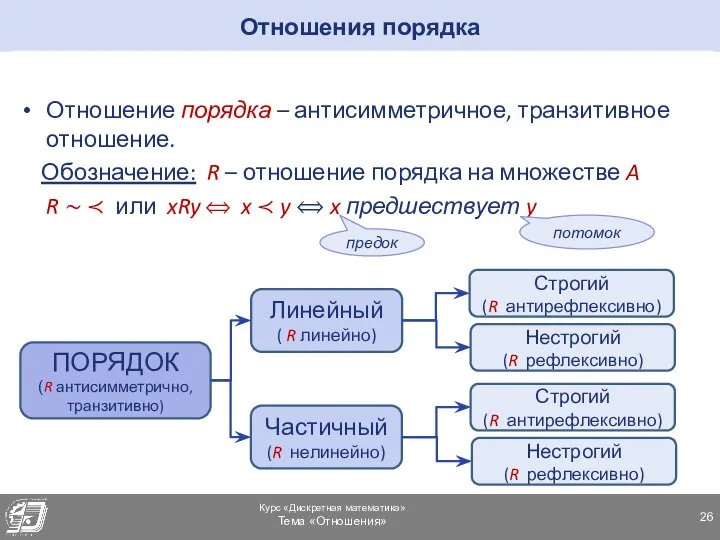
- 26. Отношения порядка Отношение порядка – антисимметричное, транзитивное отношение. Обозначение: R – отношение порядка на множестве A
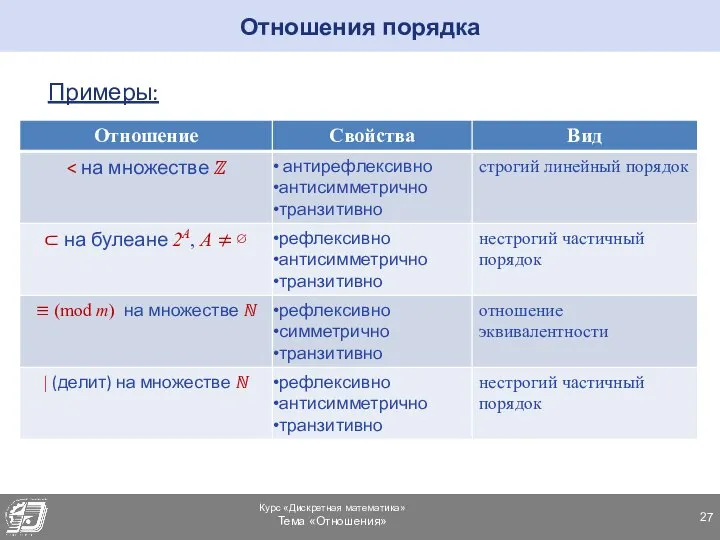
- 27. Отношения порядка Примеры:
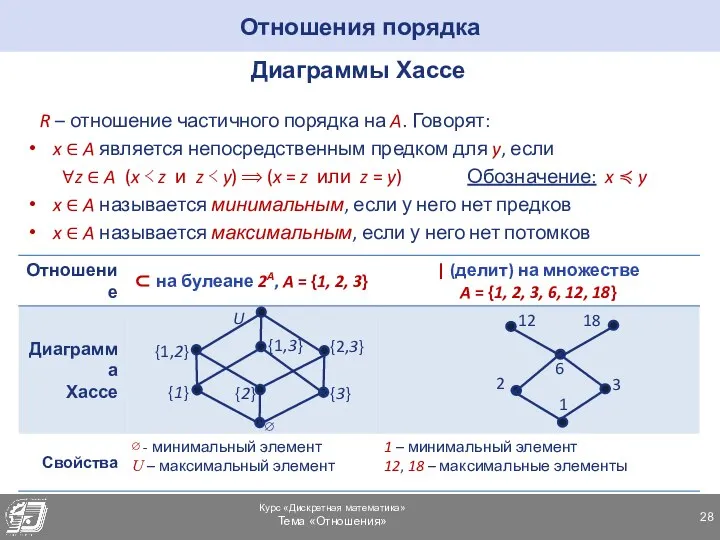
- 28. Отношения порядка Диаграммы Хассе R – отношение частичного порядка на A. Говорят: x ∈ A является
- 30. Скачать презентацию


















 Числа и точки на прямой
Числа и точки на прямой Значение логического выражения (тема № 3)
Значение логического выражения (тема № 3) Пирамида. Элементы пирамиды
Пирамида. Элементы пирамиды Презентация на тему Движение. Виды движения
Презентация на тему Движение. Виды движения  Результаты пробных ЕГЭ по математике (2013-2014 учебный год)
Результаты пробных ЕГЭ по математике (2013-2014 учебный год) Урок математики (2 класс)
Урок математики (2 класс) Введение в компьютерный и интеллектуальный анализ данных (ВКИАД)
Введение в компьютерный и интеллектуальный анализ данных (ВКИАД) Презентация на тему ПОНЯТИЕ ЛОГАРИФМА
Презентация на тему ПОНЯТИЕ ЛОГАРИФМА  Экстремум функции. Признак постоянства функции. Исследование на экстремум
Экстремум функции. Признак постоянства функции. Исследование на экстремум Многочлены. Обобщающий урок - путешествие
Многочлены. Обобщающий урок - путешествие Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов
Использование современных программных комплексов в расчете строительных конструкций. Получение матриц элементов Путешествие в страну дроби
Путешествие в страну дроби Классы Фиттинга с заданными свойствами операторов Локетта
Классы Фиттинга с заданными свойствами операторов Локетта Тела вращения. Цилиндр
Тела вращения. Цилиндр Схема Горнера. Уильям Джордж Горнер
Схема Горнера. Уильям Джордж Горнер Метод изучения длины
Метод изучения длины Основные принципы комбинаторики
Основные принципы комбинаторики Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование
Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование Решение логарифмических неравенств с помощью метода рационализации
Решение логарифмических неравенств с помощью метода рационализации Состав числа. Тренажер. Старшая группа
Состав числа. Тренажер. Старшая группа Перпендикуляр и наклонная
Перпендикуляр и наклонная Математика. Прямоугольник
Математика. Прямоугольник Практическое занятие Числа
Практическое занятие Числа Решение систем линейных уравнений способом уравнивания коэффициентов (способ сложения)
Решение систем линейных уравнений способом уравнивания коэффициентов (способ сложения) Устный счёт. 3 класс
Устный счёт. 3 класс Действия с дробями. Многогранники
Действия с дробями. Многогранники Параллельность прямых в пространстве
Параллельность прямых в пространстве Теорема Пифагора для пятиклассников
Теорема Пифагора для пятиклассников