Содержание
- 2. Теорема Пуассона Биномиальная случайная величина с параметрами N и p. Пусть число N неограниченно возрастает, при
- 3. Предельный переход при N → ∞ Вынесем общий множитель, не содержащий N
- 4. a = N p Параметр распределения Пуассона равен произведению параметров распределения Бернулли: Вывод: при большом значении
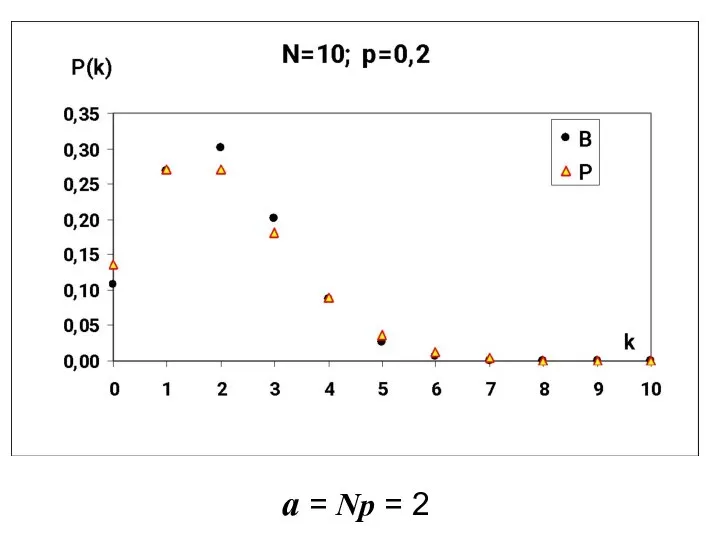
- 5. a = Np = 2
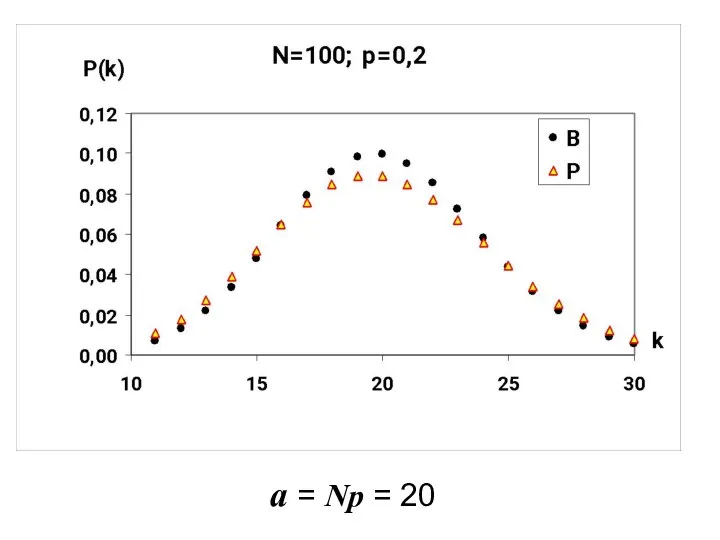
- 6. a = Np = 20
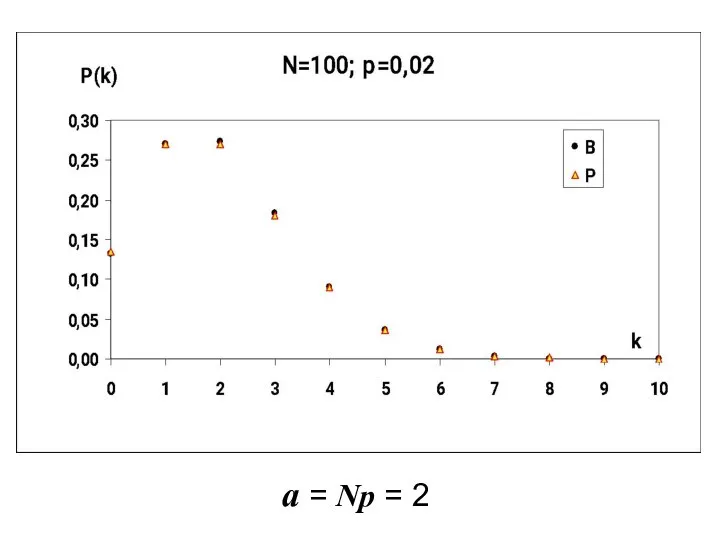
- 7. a = Np = 2
- 8. Хорошее совпадение распределения Бернулли с распределением Пуассона наблюдается при значении параметра N > 100 , и
- 9. Теорема Муавра – Лапласа Биномиальная случайная величина с параметрами N и p. Вероятность того, что значение
- 10. где: μ = Np, σ2 = Np(1– p) Согласно теореме Муавра – Лапласа, справедлив следующий предельный
- 11. Это означает, что при очень больших значениях параметра N и при большом значении произведения параметров Np
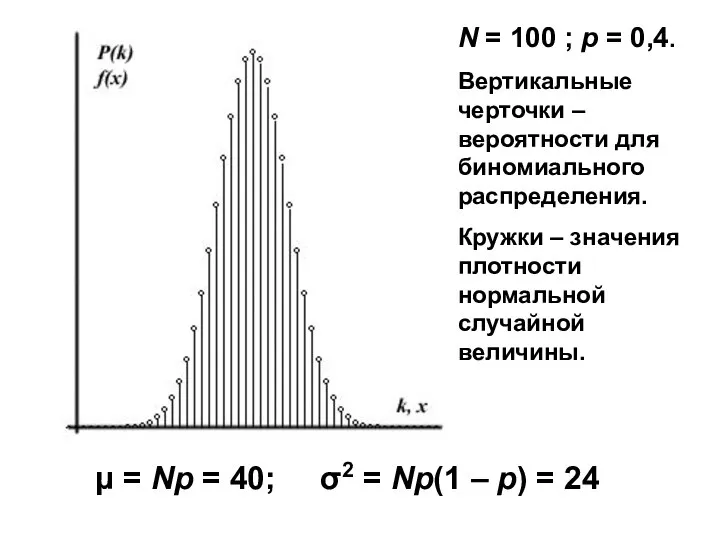
- 12. N = 100 ; p = 0,4. Вертикальные черточки – вероятности для биномиального распределения. Кружки –
- 13. Как вычислить определенный интеграл в правой части теоремы Муавра-Лапласа? Замена переменной: z = (x – μ)
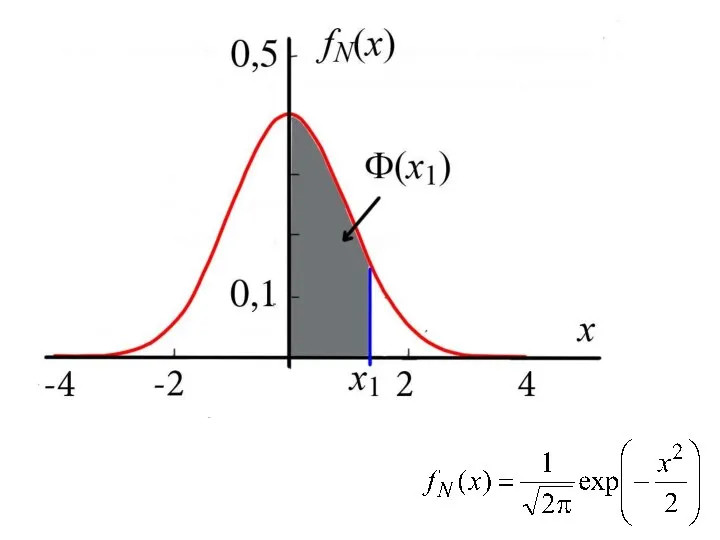
- 14. Функция Лапласа Интеграл с переменным верхним пределом от нормированной функции Гаусса Это плотность гауссовой случайной величины
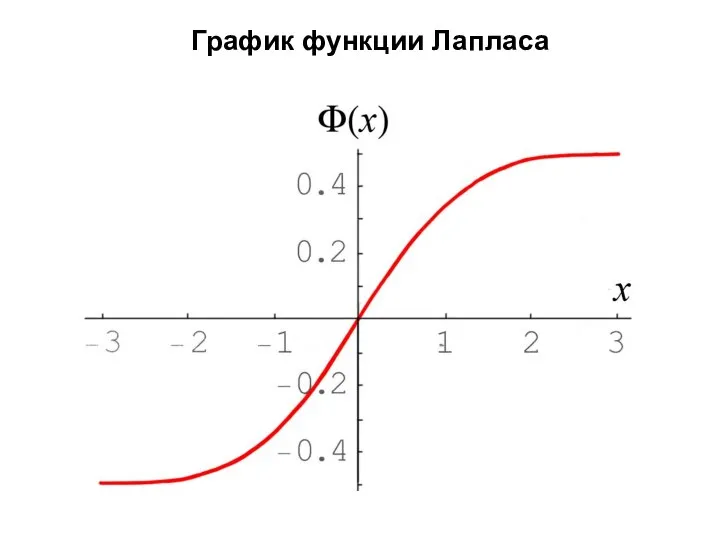
- 15. Свойства функции Лапласа Φ(x=0) = 0 2. Φ(−x) = − Φ(x). 3. Функция Лапласа быстро стремится
- 17. График функции Лапласа
- 18. k - значение биномиальной случайной величины с параметрами N и p. где Ф – функция Лапласа,
- 19. Центральная предельная теорема
- 20. i ; (i = 1, …, N ) – случайные величины Если N → ∞, то
- 21. Теорема 1 i ; (i = 1, …, N ) – попарно независимые случайные величины, имеющие
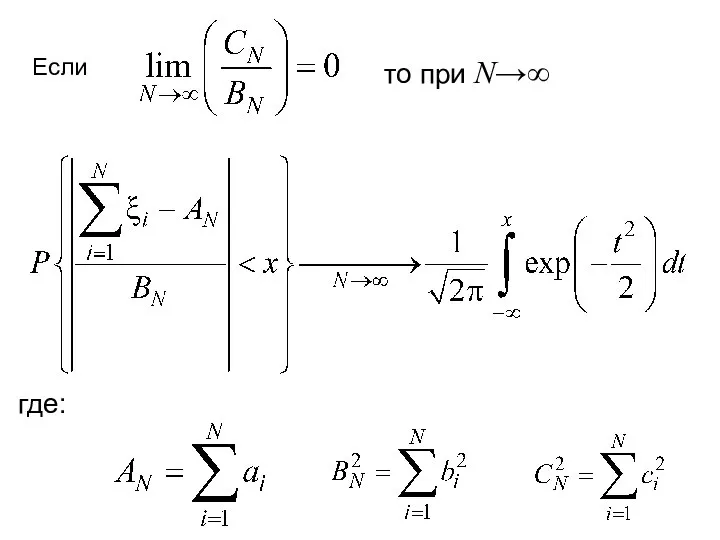
- 22. Теорема 2 (теорема Ляпунова) i ; (i = 1, …, N ) – независимые случайные величины.
- 23. Если то при N→∞ где:
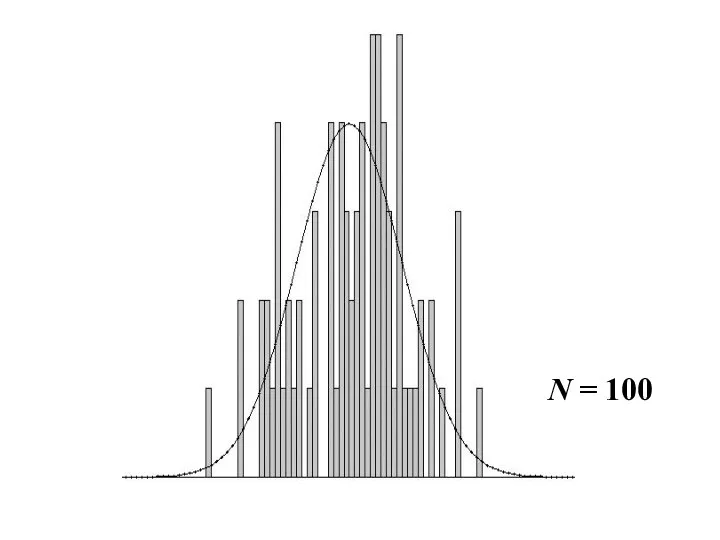
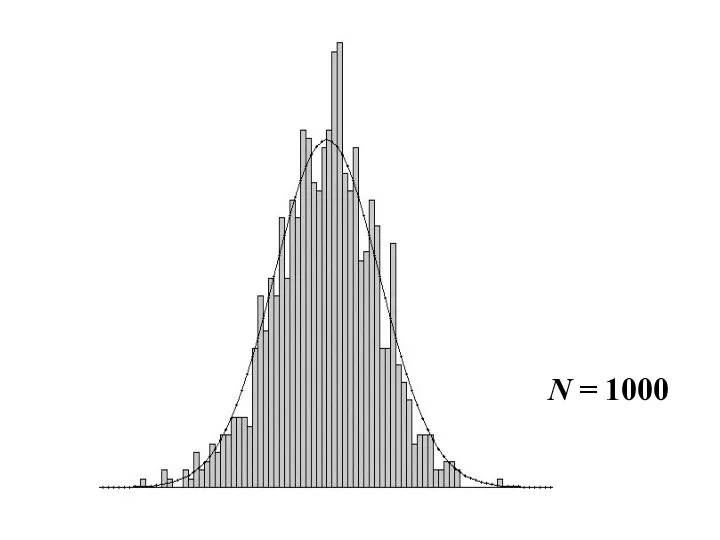
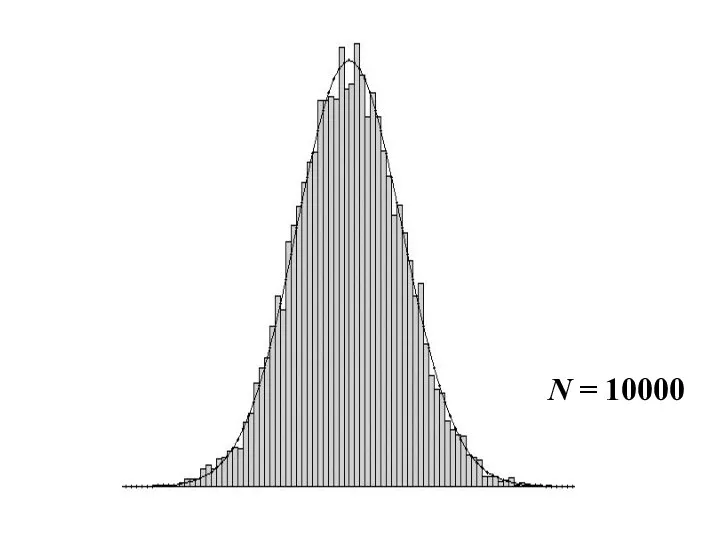
- 24. Нормированная сумма любых независимых случайных величин при N→∞ имеет нормальное распределение. На следующих слайдах показаны графики
- 25. N = 100
- 26. N = 1000
- 27. N = 10000
- 29. Скачать презентацию
















 Системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной Системы неравенств с двумя переменными
Системы неравенств с двумя переменными ЕГЭ. Экономические задачи VI
ЕГЭ. Экономические задачи VI Шар и сфера
Шар и сфера Теорема Пифагора
Теорема Пифагора Повторение темы Параллельные прямые
Повторение темы Параллельные прямые Фалес Милетский - один из первых геометров
Фалес Милетский - один из первых геометров Составление примеров на сложение
Составление примеров на сложение Функции и литература
Функции и литература Кратные числа
Кратные числа Декартова система координат
Декартова система координат Деление дробей. Взаимно-обратные числа
Деление дробей. Взаимно-обратные числа Гомотетия. Подобие фигур
Гомотетия. Подобие фигур Двоичная арифметика
Двоичная арифметика Теорема Пифагора
Теорема Пифагора Параллелограмм и трапеция. Урок 3
Параллелограмм и трапеция. Урок 3 Разбор задачи 3.33 (Катышев, Магнус - Сборник задач по начальному курсу эконометрики)
Разбор задачи 3.33 (Катышев, Магнус - Сборник задач по начальному курсу эконометрики) Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников 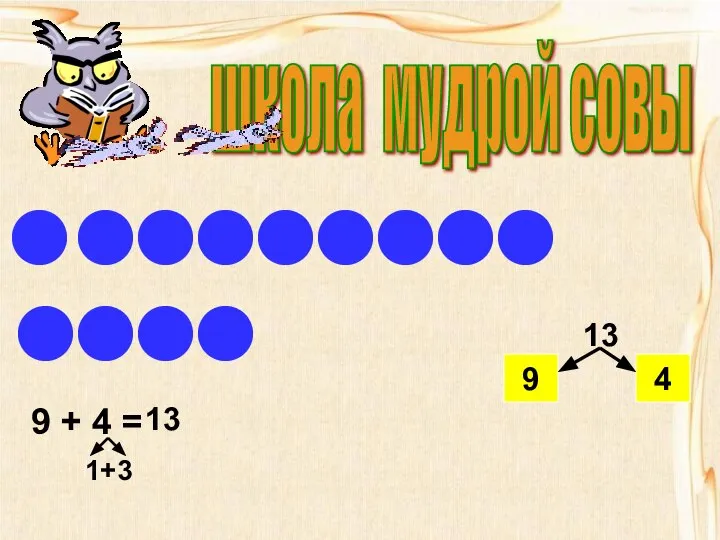 Состав числа 13
Состав числа 13 Теорема Пифагора
Теорема Пифагора Решение систем линейных алгебраических уравнений
Решение систем линейных алгебраических уравнений Математическая игра Отгадайка
Математическая игра Отгадайка Riešenie rovníc, ak je neznáma na oboch stranách rovnice
Riešenie rovníc, ak je neznáma na oboch stranách rovnice Циклоида, эпициклоида
Циклоида, эпициклоида Многоэтажные дроби. 8 класс
Многоэтажные дроби. 8 класс Римская нумерация
Римская нумерация Отношения рядом стоящих чисел в пределах 10
Отношения рядом стоящих чисел в пределах 10 Презентация на тему Число и цифра 2 (1 класс)
Презентация на тему Число и цифра 2 (1 класс)