Содержание
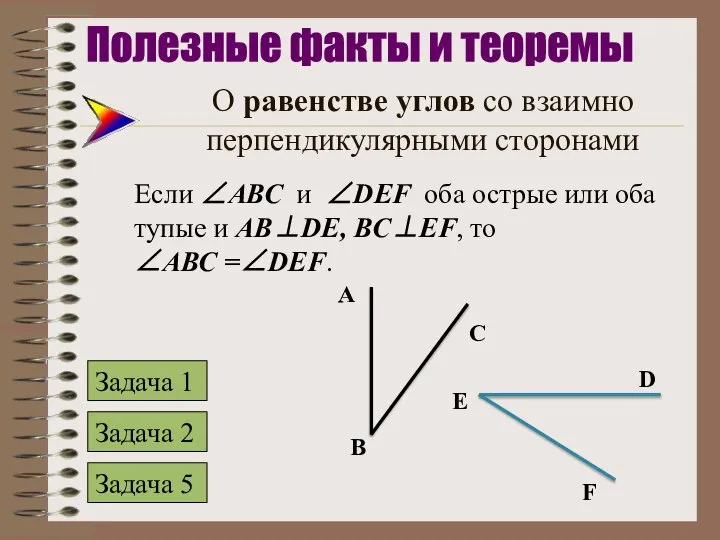
- 2. О равенстве углов со взаимно перпендикулярными сторонами Если ∠АВС и ∠DEF оба острые или оба тупые
- 3. О точках пересечения медиан, биссектрис, высот треугольника Три биссектрисы треугольника пересекаются в одной точке. Три высоты
- 4. Свойства средней линии трапеции Средняя линия параллельна основаниям трапеции. Средняя линия (и только она) делит пополам
- 5. Свойство медианы в прямоугольном треугольнике В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине. Если
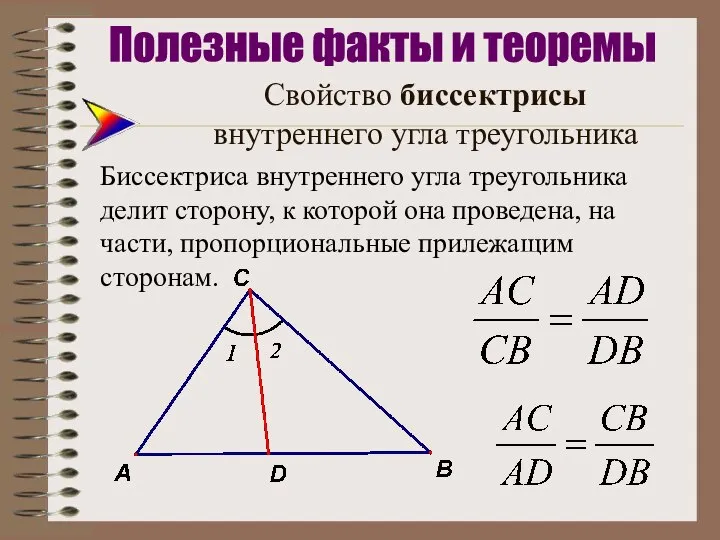
- 6. Свойство биссектрисы внутреннего угла треугольника Биссектриса внутреннего угла треугольника делит сторону, к которой она проведена, на
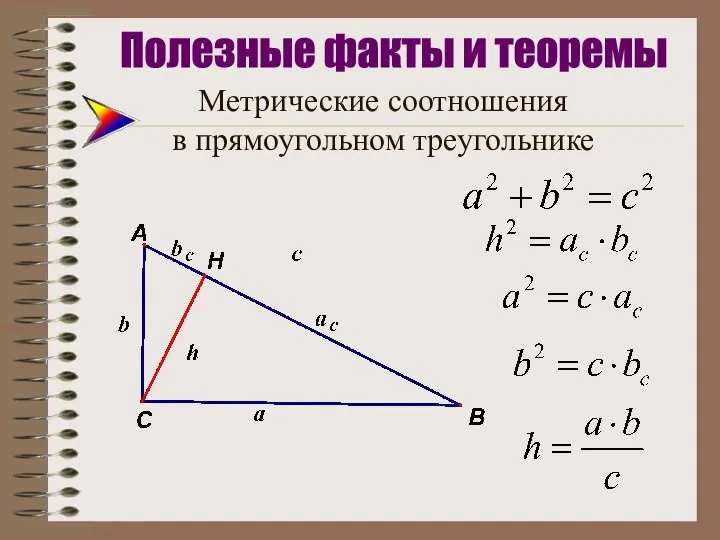
- 7. Метрические соотношения в прямоугольном треугольнике Полезные факты и теоремы
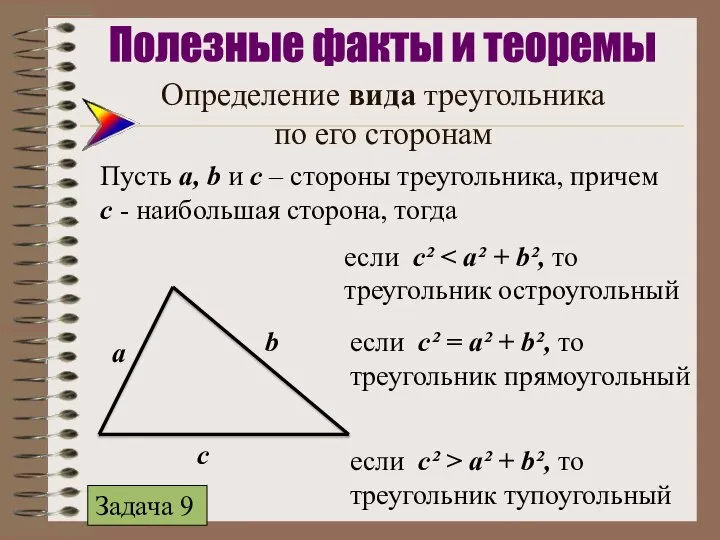
- 8. Определение вида треугольника по его сторонам Пусть а, b и с – стороны треугольника, причем с
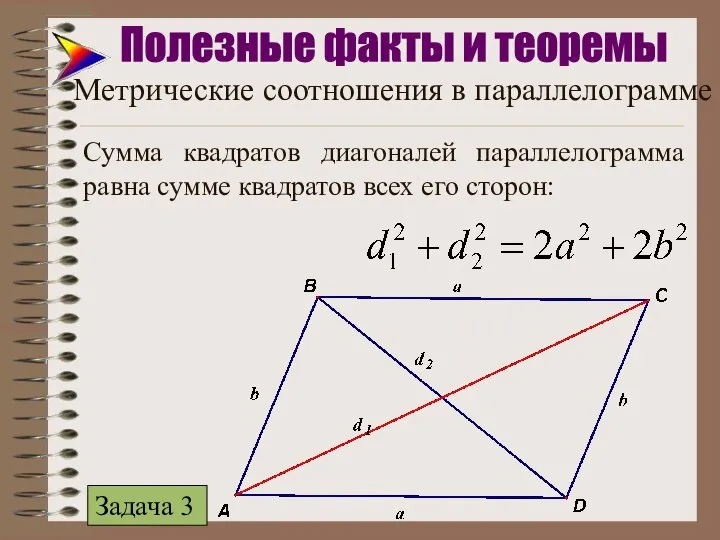
- 9. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: Полезные факты и теоремы Метрические соотношения
- 10. Если два треугольника подобны, то любой линейный элемент (или сумма линейных элементов) одного треугольника относится к
- 11. Рассмотреть эти отрезки как стороны двух треугольников и доказать, что треугольники равны. Заменить отрезок а равным
- 12. Проведение прямой, параллельной или перпендикулярной одной из имеющихся. Проведение вспомогательной биссектрисы. Дополнительные построения Удвоение медианы треугольника
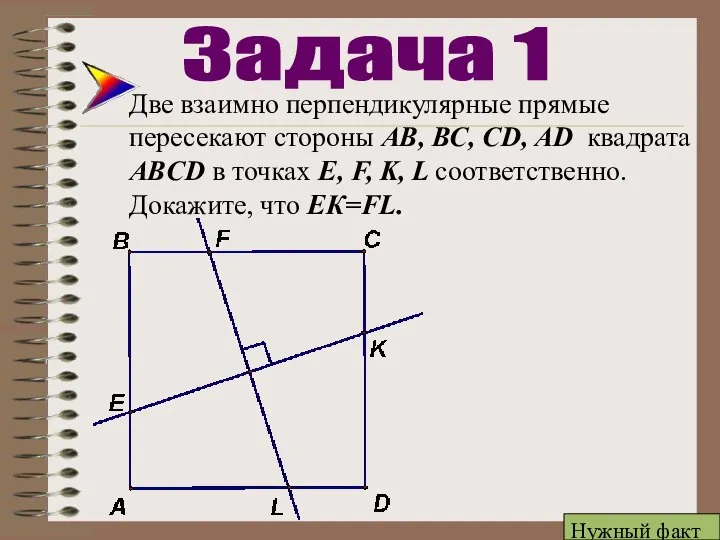
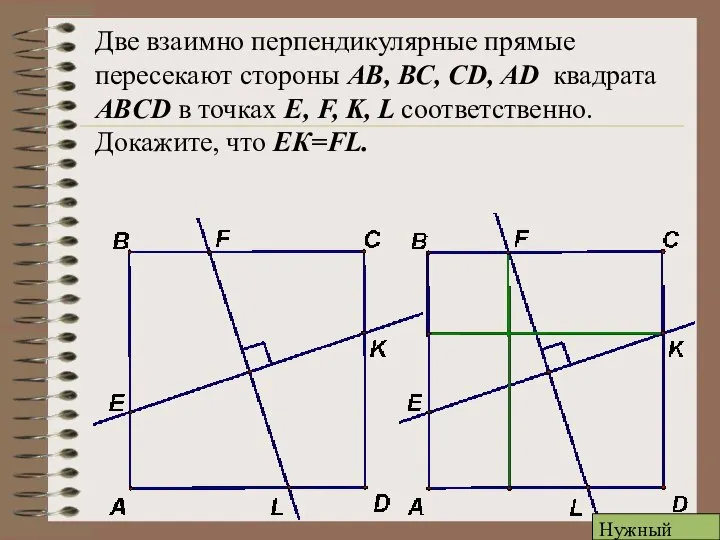
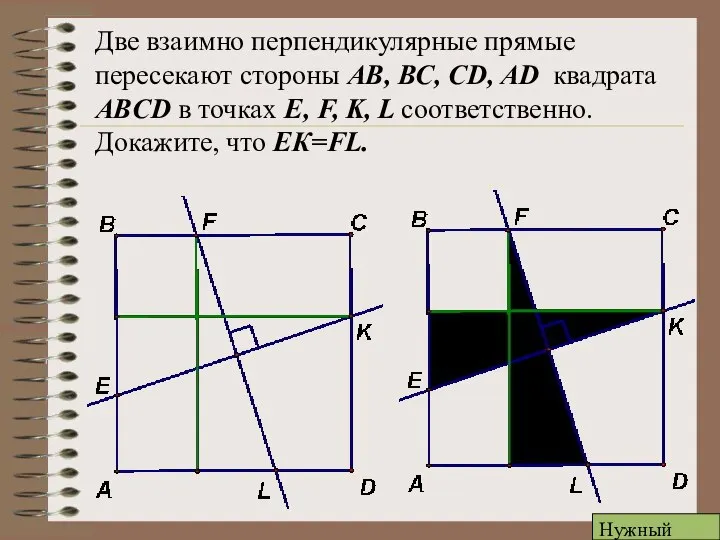
- 13. Две взаимно перпендикулярные прямые пересекают стороны АВ, ВС, CD, AD квадрата ABCD в точках E, F,
- 14. Две взаимно перпендикулярные прямые пересекают стороны АВ, ВС, CD, AD квадрата ABCD в точках E, F,
- 15. Две взаимно перпендикулярные прямые пересекают стороны АВ, ВС, CD, AD квадрата ABCD в точках E, F,
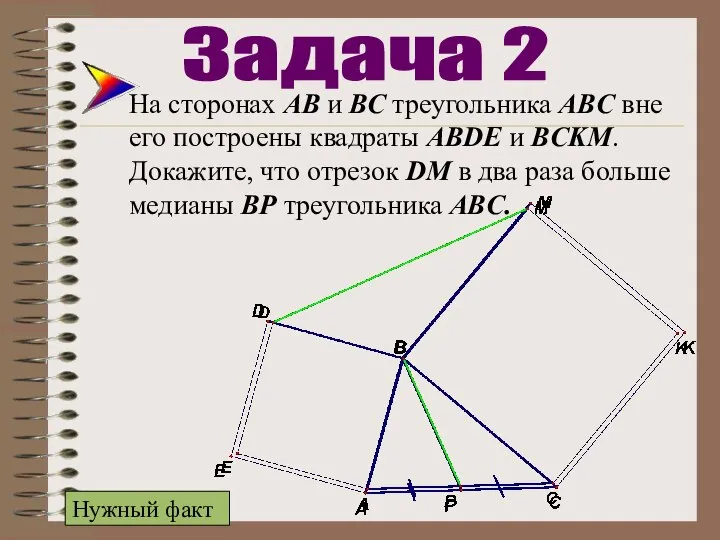
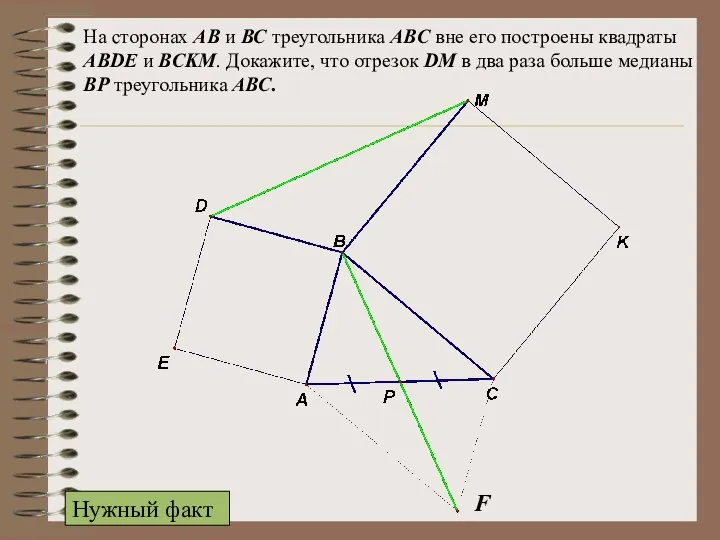
- 16. На сторонах АВ и ВС треугольника ABC вне его построены квадраты ABDE и BCKM. Докажите, что
- 17. На сторонах АВ и ВС треугольника ABC вне его построены квадраты ABDE и BCKM. Докажите, что
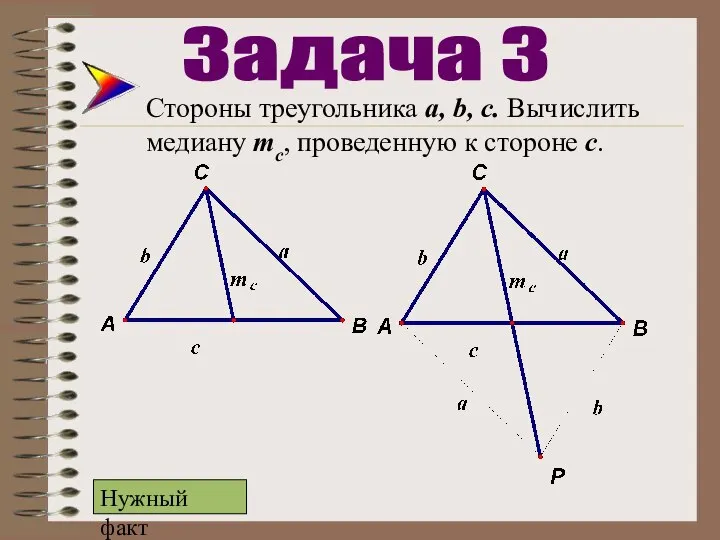
- 18. Стороны треугольника а, b, c. Вычислить медиану mc, проведенную к стороне с. Задача 3 Нужный факт
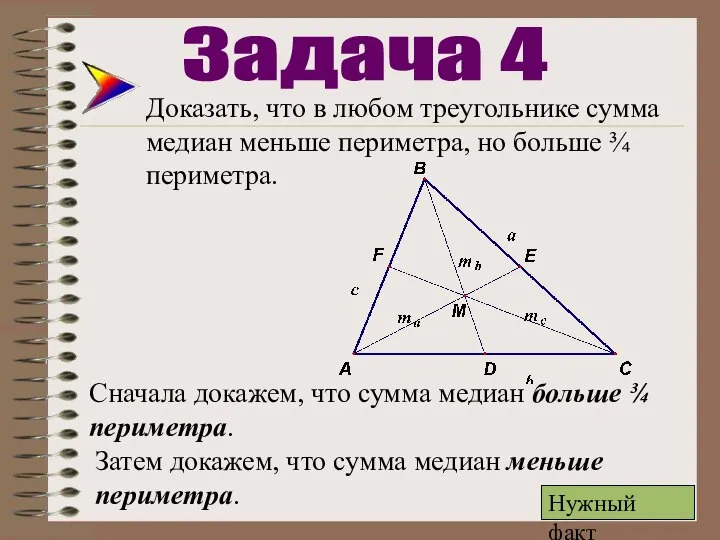
- 19. Доказать, что в любом треугольнике сумма медиан меньше периметра, но больше ¾ периметра. Задача 4 Сначала
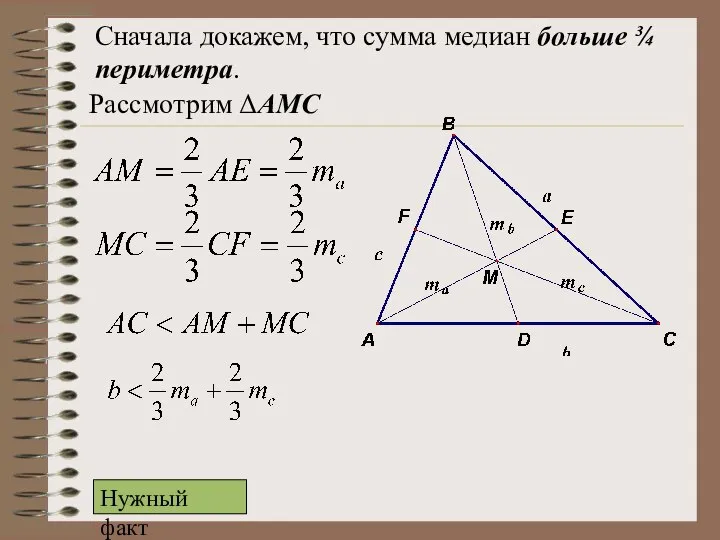
- 20. Сначала докажем, что сумма медиан больше ¾ периметра. Рассмотрим ΔАМС Нужный факт
- 21. Рассмотрим ΔBМС: Рассмотрим ΔABМ:
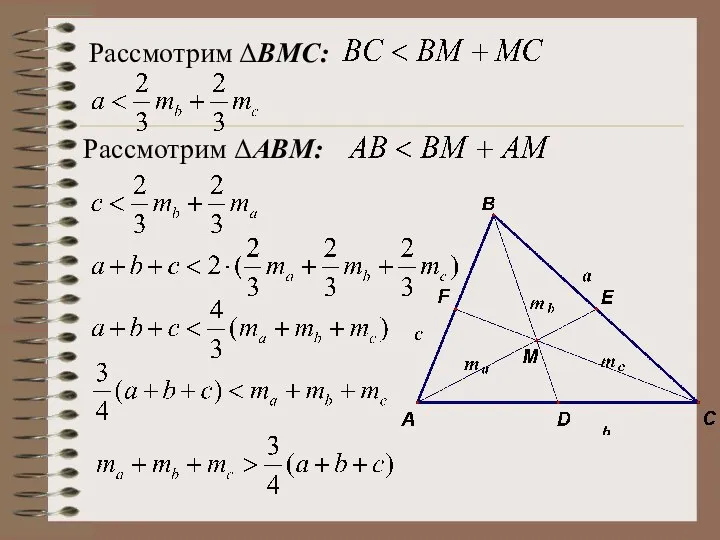
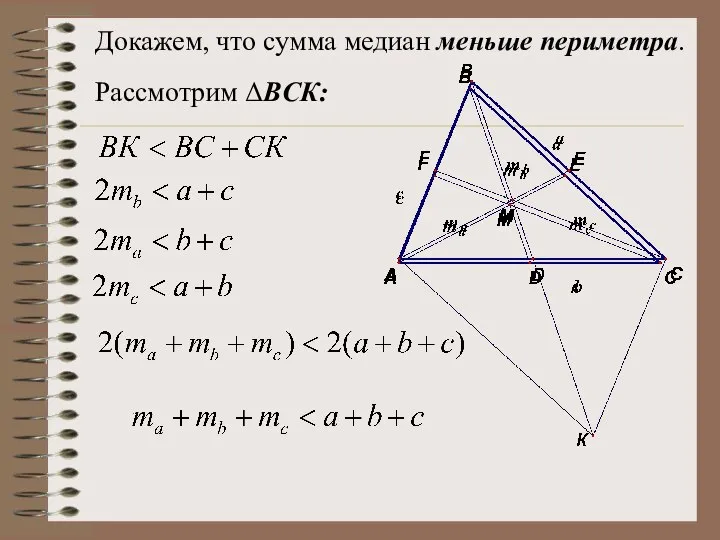
- 22. Докажем, что сумма медиан меньше периметра. Рассмотрим ΔBСК:
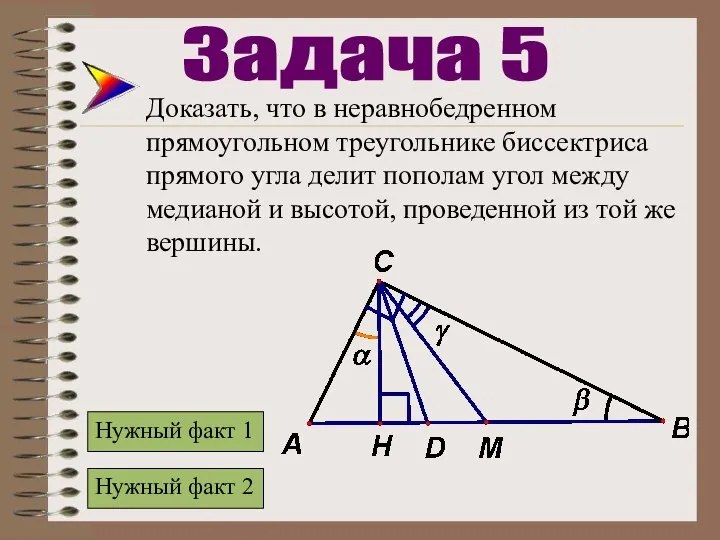
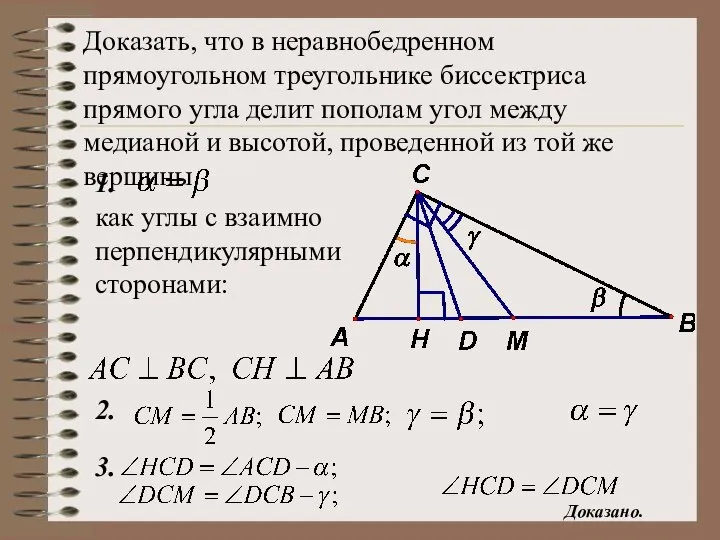
- 23. Доказать, что в неравнобедренном прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой,
- 24. Доказать, что в неравнобедренном прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой,
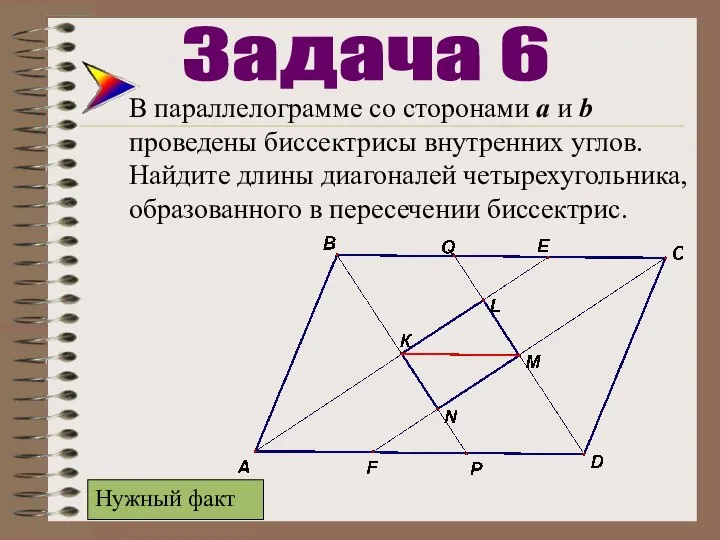
- 25. В параллелограмме со сторонами а и b проведены биссектрисы внутренних углов. Найдите длины диагоналей четырехугольника, образованного
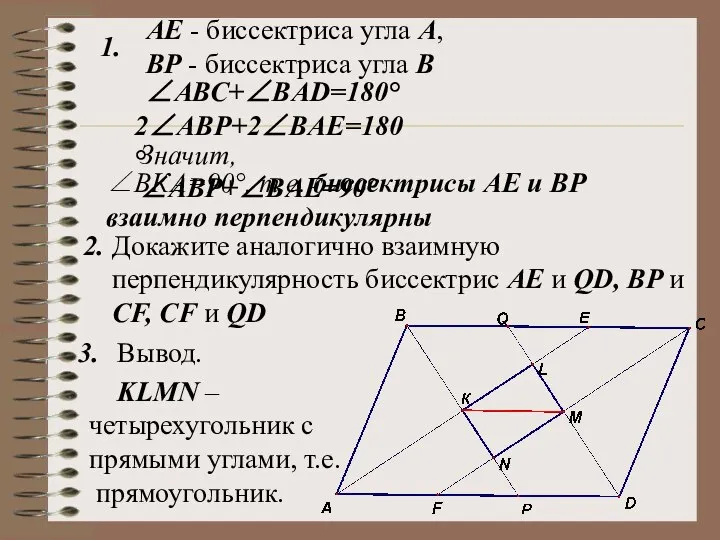
- 26. АЕ - биссектриса угла А, ВР - биссектриса угла В 1. 2. KLMN – четырехугольник с
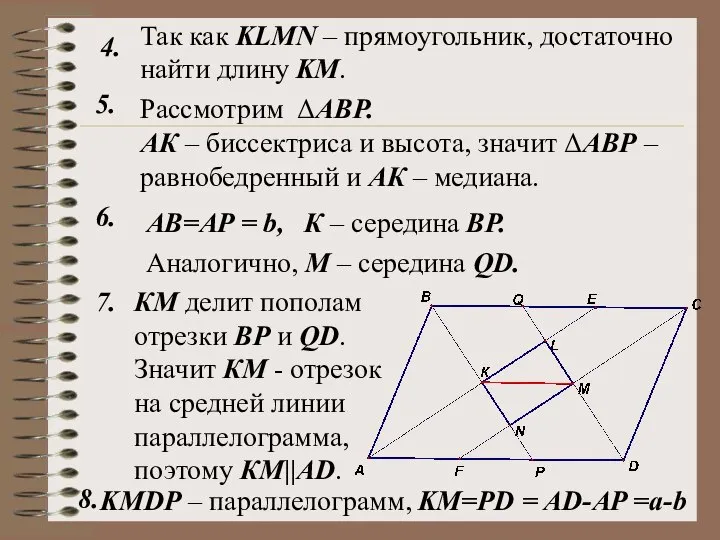
- 27. Рассмотрим ΔАВР. 4. 5. Так как KLMN – прямоугольник, достаточно найти длину KM. 7. KM=PD =
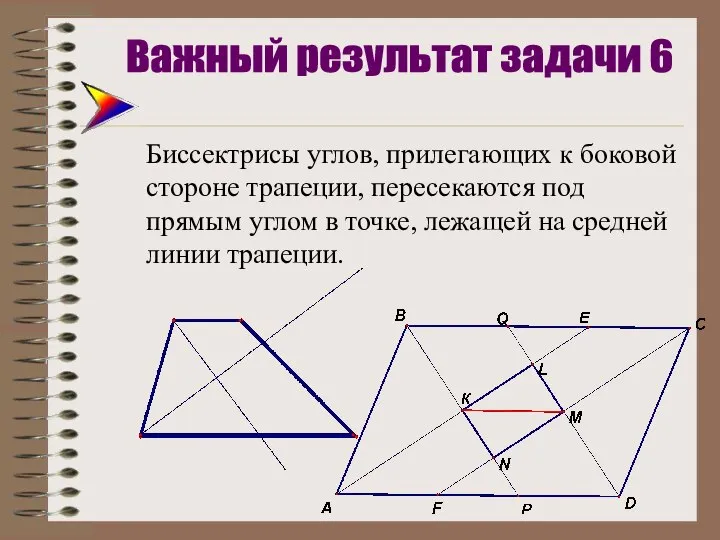
- 28. Биссектрисы углов, прилегающих к боковой стороне трапеции, пересекаются под прямым углом в точке, лежащей на средней
- 29. Основным методом составления уравнений в геометрических задачах является метод опорного элемента. Он заключается в том, что
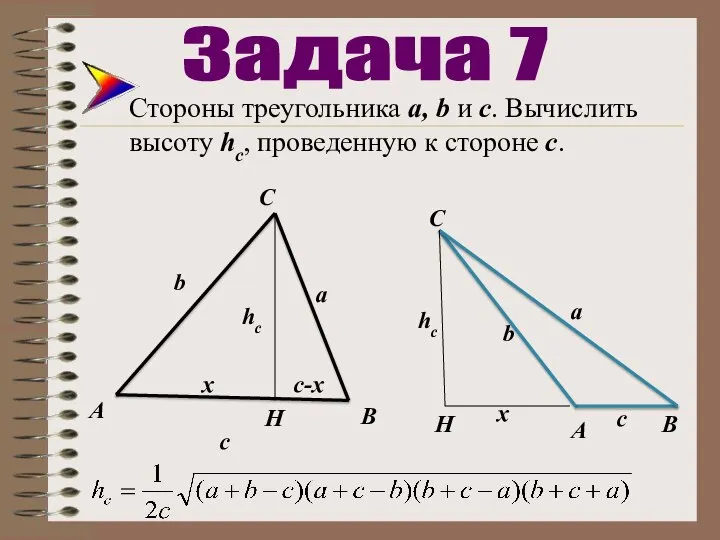
- 30. Стороны треугольника а, b и с. Вычислить высоту hc, проведенную к стороне с. Задача 7 x
- 31. Если в задаче требуется найти отношение каких-либо величин, то она решается методом введения вспомогательного параметра. В
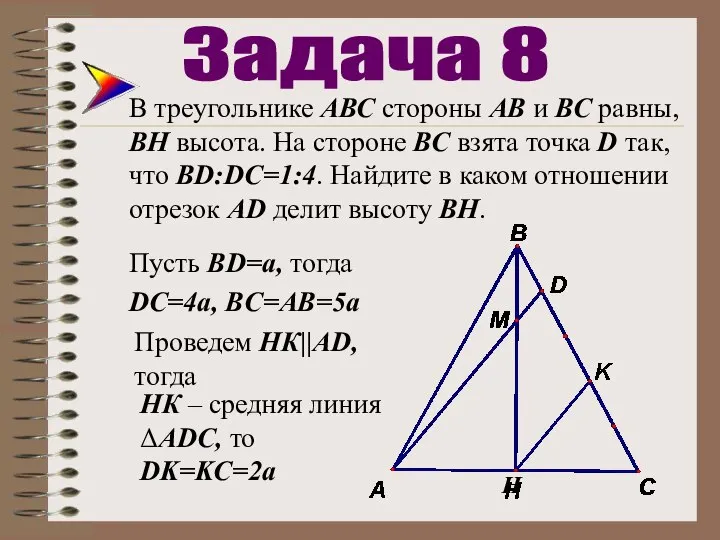
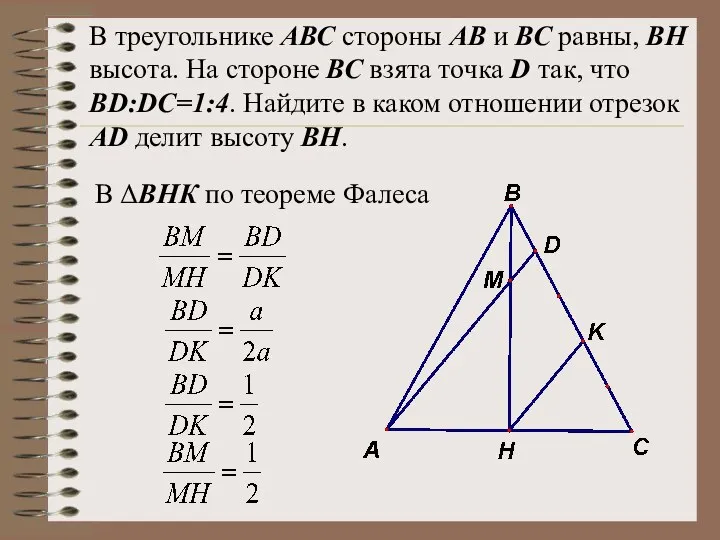
- 32. В треугольнике АВС стороны АВ и ВС равны, ВН высота. На стороне ВС взята точка D
- 33. В треугольнике АВС стороны АВ и ВС равны, ВН высота. На стороне ВС взята точка D
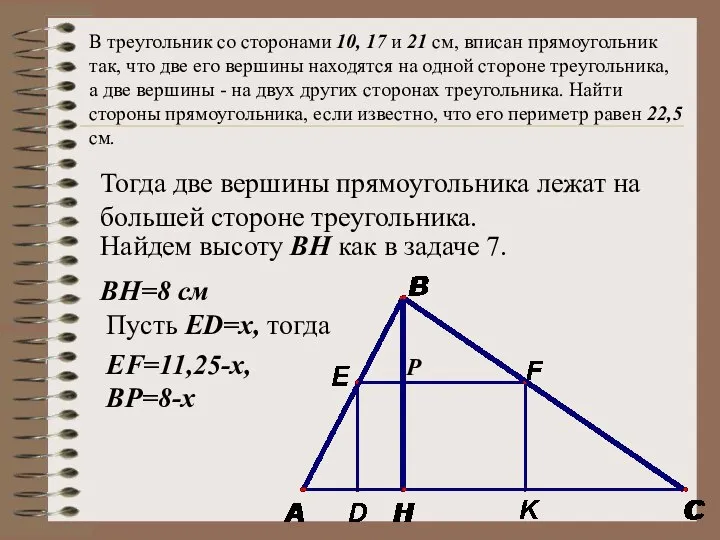
- 34. В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольник так, что две его вершины
- 35. В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольник так, что две его вершины
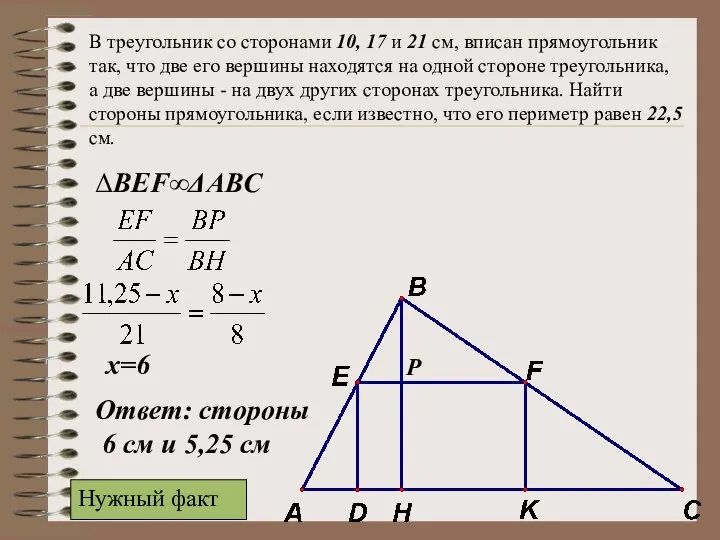
- 36. В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольник так, что две его вершины
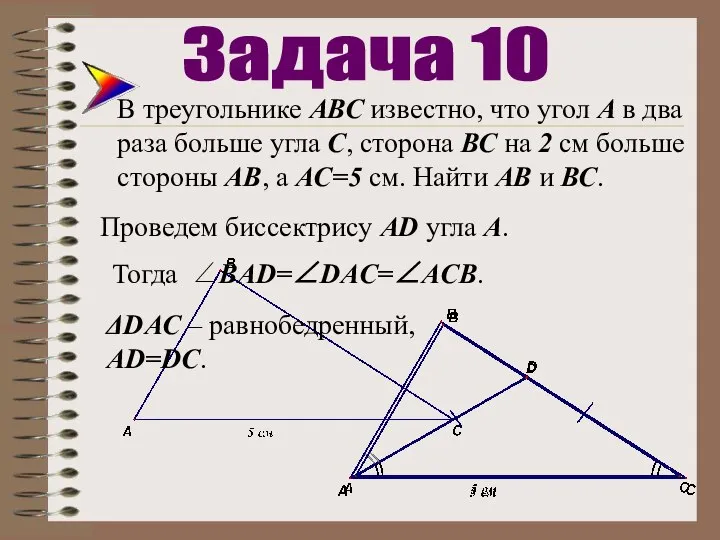
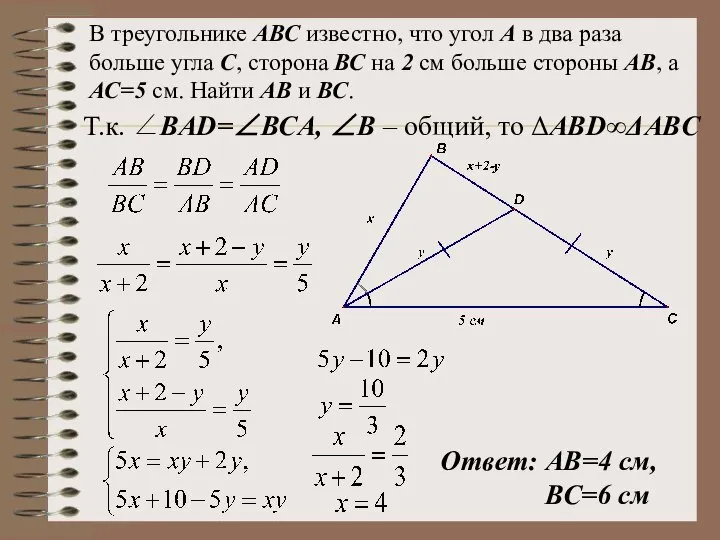
- 37. В треугольнике АВС известно, что угол А в два раза больше угла С, сторона ВС на
- 38. В треугольнике АВС известно, что угол А в два раза больше угла С, сторона ВС на
- 40. Скачать презентацию









 Задание 7. Простейшие текстовые задачи
Задание 7. Простейшие текстовые задачи Учим состав чисел с Колобком
Учим состав чисел с Колобком График линейной функции
График линейной функции Равносильные уравнения и неравенства
Равносильные уравнения и неравенства Пушкин и математика
Пушкин и математика Презентация на тему ТОЧКИ И ЛИНИИ. ПРЯМАЯ
Презентация на тему ТОЧКИ И ЛИНИИ. ПРЯМАЯ  Умножение, деление и возведение в степень алгебраических дробей и А.С. Пушкин в Михайловском
Умножение, деление и возведение в степень алгебраических дробей и А.С. Пушкин в Михайловском Симметрия. Что объединяет эти изображения?
Симметрия. Что объединяет эти изображения? Числовые и буквенные выражения
Числовые и буквенные выражения Проценты. Основные задачи на проценты
Проценты. Основные задачи на проценты Презентация на тему Собрание заданий для устного счета 3-4 класс
Презентация на тему Собрание заданий для устного счета 3-4 класс  Прогрессии
Прогрессии Треугольники
Треугольники Определение медианы
Определение медианы Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Обратные тригонометрические функции
Обратные тригонометрические функции Построение сечений
Построение сечений Приёмы устных вычислений в пределах 1000
Приёмы устных вычислений в пределах 1000 Сравнение множеств
Сравнение множеств Арифметическая прогрессия
Арифметическая прогрессия Способы задания арифметической прогрессии
Способы задания арифметической прогрессии НОМЕР 18
НОМЕР 18 Решение задач и примеров
Решение задач и примеров Применение производной к исследованию функций
Применение производной к исследованию функций Формулы сложных процентов в задачах с финансово-экономическим содержанием
Формулы сложных процентов в задачах с финансово-экономическим содержанием Тела вращения в природе
Тела вращения в природе Занимательная математика
Занимательная математика