Транспортная задача. Методы нахождения начального решения транспортной задачи

Транспортная задача
Транспортная задача - это математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов с минимизацией затрат на перемещение.
Существует несколько методов решения транспортной задачи. Два из них:
решение транспортной задачи методом потенциалов (будем использовать)
решение транспортной задачи с использованием симплекс метода.
Решение задачи методом потенциалов происходит в несколько этапов:
Определение опорного решения.
Применение к найденному опорному решению самого метода потенциалов.
Проверка единственности решения.
Определение опорного плана, в свою очередь, можно выполнить несколькими способами. Рассмотрим два из них:
метод северо-западного угла
метод минимальных стоимостей

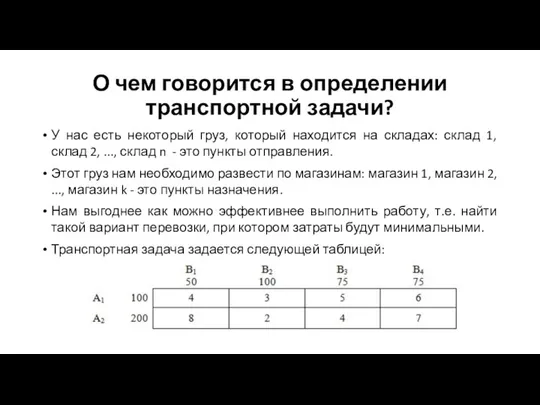
О чем говорится в определении транспортной задачи?
У нас есть некоторый груз, который находится на складах: склад 1, склад 2, ..., склад n - это пункты отправления.
Этот груз нам необходимо развести по магазинам: магазин 1, магазин 2, ..., магазин k - это пункты назначения.
Нам выгоднее как можно эффективнее выполнить работу, т.е. найти такой вариант перевозки, при котором затраты будут минимальными.
Транспортная задача задается следующей таблицей:

Что означают числа в условии транспортной задачи?
два склада с товаром: А1 и А2
объем товара - на складах А1 и А2
пунктами назначения - В1, В2, В3 и В4
потребности пунктов назначения
матрица стоимостей (расценки) перевозки 1 единицы груза из соответствующих пунктов; расстояния между соответствующими пунктами.

Метод северо-западного угла
Заполнение таблицы начинается с самой верхней левой (северо-западной) ячейки.
Перед тем, как распределять ресурсы по "магазинам", проверим, равны ли общие потребности имеющимся ресурсам?
Потребности: 50 + 100 + 75 + 75 = 300
Ресурсы: 100 + 200 = 300
Потребности = Ресурсам
В этом случае говорят, что транспортная задача закрытая.

Метод северо-западного угла
Начнем нахождение опорного решения:
В магазин В1 требуется 50 единиц товара. Со склада А1 отправим в этот магазин 50 единиц.
Потребности магазина В1 выполнены, следовательно, нет необходимости везти туда груз со склада А2.
На складе А1 еще осталось 50 единиц груза. Эти остатки можем направить в магазин В2. Ресурсы склада А1 исчерпаны.

Метод северо-западного угла
Переходим к складу А2.
Так как потребности магазина В1 выполнены полностью, рассмотрим магазин В2, которому требуется 100-50=50 единиц товара. Направим их туда.
Заметим, на складе А2 осталось еще 200-50=150 единиц груза, которые мы распределим по магазинам В3 и В4, полностью удовлетворяя и их потребности.
Склады пусты!
Потребности магазинов в товаре полностью выполнены!
Получен опорный (первоначальный) план транспортной задачи.

Метод минимальных стоимостей получения опорного плана
Суть метода состоим в том, чтобы в первую очередь направлять груз в те пункты, где "расценки" в матрице стоимостей минимальны. Если клеток с наименьшими тарифами несколько, то заполняется любая из них.
Направляем 100 единиц груза из склада А2 в магазин В2.
Остатки на складе А2 — 100 единиц. Потребности магазина В2 выполнены.
Груз со склада А2 отправим в магазин, у которого стоимость перевозки ниже — магазин В3, так как мин(4;7)=4
Размер поставки равен потребности магазина — 75. Остатки со склада 200-100-75=25 перенесем в магазин В4.

Метод минимальных стоимостей получения опорного плана
Остается только раскидать груз со склада А1 по магазинам: В1 — 50 единиц, В4 — 75-25=50 единиц.
Получили два опорных плана: методом северо-западного угла и методом минимальных стоимостей.
Первый опорный план (по методу северо-западного угла):
Второй опорный план (по методу минимальных стоимостей):

Проверка правильности вычисления первоначального плана
Правило:
Количество заполненных клеток (базисных клеток) в первоначальном плане ВСЕГДА должно быть равно m + n - 1, где m - количество строк, n - количество столбцов
В нашем случае условие выполняется: 2 + 4 - 1 = 5
Во избежании случайных вычислительных ошибок проверим, равны ли суммарные значения каждой строки и каждого столбца соответствующим значениям условия.
100 = 50 + 50
200 = 100 + 75 + 25
По столбцам:
Суммарные значения элементов каждого столбца равны соответствующим потребностям магазинов.
Несмотря на то, что опорные планы разные, оба приведут к одному оптимальному решению или же к решениям, имеющим одну стоимость перевозки.

Метод потенциалов решения транспортной задачи - шаг 1
Начнем с проверки опорного плана на оптимальность.
Выпишем матрицу стоимостей, данную в условии задачи.
Далее строим рядом две таблицы. Размерность таблиц как и в матрице стоимостей:
количество строк = количеству складов, количество столбцов = количеству магазинов.
Заполняем первую — левую таблицу в соответствии с полученным опорным планом.

Метод потенциалов решения транспортной задачи - шаг 1
Переходим в правую таблицу.
Переносим из матрицы стоимостей значения, которые соответствуют занятым клеткам левой таблицы.
В матрице стоимости эти значения подчеркнуты.
Припишем каждой строке правой таблице потенциалы u1, u2. Каждому столбцу — потенциалы v1, v2, v3, v4.

Метод потенциалов решения транспортной задачи - шаг 1
Для вычисления этих потенциалов в некоторых учебниках составляют систему и из нее определяют неизвестные.
Будем определять значения потенциалов непосредственно из правой таблицы.
Составим систему уравнений по следующему правилу:
Каждое из значений в ячейке (правая таблица) равно сумме потенциалов соответствующей строки и соответствующего столбца.
Например: значение 4 находится в 1-й строке и 1-м столбце. Тогда сумма потенциалов 1-й строки (u1) и 1-ого столбца(v1) равна 4.

Метод потенциалов решения транспортной задачи - шаг 1
Первое уравнение системы: u1 + v1 = 4
Рассмотрим следующее значение таблицы.
Значение 3 находится в первой строке (потенциал u1), втором столбце (потенциал v2).
Второе уравнение системы: u1 + v2 = 3
Аналогично для каждого значения таблицы составим уравнение.
Получим систему уравнений:

Метод потенциалов решения транспортной задачи - шаг 1
Для того, чтобы система имела единственное решение, примем значение одного из потенциалов равным нулю.
Для удобства в качестве этого потенциала всегда будем брать v4.
Тогда система уравнений будет выглядеть:
Решим систему уравнений и получим значения потенциалов:

Метод потенциалов решения транспортной задачи - шаг 1
Наглядно:
Так как система очень проста, то значения потенциалов можно получить и устно.
Подробно:
Сумма отмеченных потенциалов равна 7, следовательно, потенциал u2 = 7
Значение 4 базисной ячейки находится во 2-й строке, 3-м столбце, тогда рассмотрим сумму соответствующих потенциалов.
v3 + 7 = 4 откуда v3 = -3

Метод потенциалов решения транспортной задачи - шаг 1
Далее все аналогично:
Значение 2 равно сумме потенциалов 2-й строки и 2-го столбца:
2 = v2 + 7 откуда v2 = -5
u1 - 5 = 3, откуда u1 = 8
v1 + 8 = 4, откуда v1 = -4
В итоге получили:

Метод потенциалов решения транспортной задачи - шаг 1
Далее приступим к заполнению пустых ячеек (свободные ячейки) правой таблицы.
Свободные ячейки подчиняются тому же правилу суммирования потенциалов.
Вычислим оценочную матрицу, по которой узнаем, оптимален ли рассматриваемый план.
Из каждого элемента матрицы стоимостей вычтем соответствующий элемент правой таблицы:
Получили оценочную матрицу. Заметим, что в базисных ячейках всегда получим нули.

Метод потенциалов решения транспортной задачи - шаг 1
Критерий оптимальности:
если в оценочной матрице нет отрицательных элементов, то решение оптимально, в противном случае решение не оптимально.
Согласно критерию оптимальности, решение выше не оптимально, так как в оценочной таблице присутствует отрицательное значение.
Дабы не загромождать решение множеством таблиц, оценочная матрица в нашем решении будет "вписана" в правую таблицу.
Подчеркнутые значения - базисные ячейки, как сказано выше, значения оценочной матрицы в базисных ячейках равны нулю, нули писать не будем. Выделенные значения - значения оценочной матрицы в свободных ячейках, среди них ищем отрицательные значения.
Для перехода к следующему опорному решению выполним следующее (построим цикл пересчета):
- найдем среди отрицательных значений оценочной матрицы максимальный по модулю (или по другому, минимальный среди отрицательных)
- в соответствующей ячейке левой таблицы ставим знак " + "

Метод потенциалов решения транспортной задачи - шаг 1
В нашем примере наименьшее отрицательное значение -2.
Знак " + " ставим в ячейке 1-й строки, 4-го столбца левой таблицы - ячейка соответствующая значению (-2).
Необходимо расставить чередующиеся значения "+ " и " — " в левой таблице так, чтобы получился замкнутый цикл и выполнялись правила:
- остальные знаки цикла (все кроме уже поставленного первого " + ") ставим только в заполненных (базисных) ячейках таблицы,
- если в строке есть "плюс" ("минус"), то в этой строке должен быть и "минус" ("плюс"),
- если в столбце есть " плюс" ("минус"), то в этом столбце должен быть и "минус" ("плюс").
Применим к нашей таблице:
В столбце В4 есть "плюс", следовательно в этом столбце должен быть и "минус".

Метод потенциалов решения транспортной задачи - шаг 1
Аналогично, в строке А2 есть "минус", следовательно должен быть и "плюс".
Если мы поставим этот "плюс" в столбце В3, то цепочка порвется, так как в этом же столбце невозможно поставить "минус" — нет заполненной ячейки.
Ставим " + " в столбце В2 и продолжаем чередовать знаки.
Получили замкнутый цикл чередующихся знаков. Цикл пересчета найден!
Общее количество заполненных (базисных) ячеек при пересчете не должно изменится!
Получили следующий опорный план:

Метод потенциалов решения транспортной задачи - шаг 1
Вычислим стоимость перевозки на первом шаге.
Для этого найдем сумму произведений значений опорного плана и матрицы стоимостей.
S1 = 50 · 4 + 100 · 2 + 75 · 4 + 25 · 7 + 50 · 6 = 1275
На первом шаге решения транспортной задачи получили опорный план:
Общая стоимость перевозки S1 = 1275

Метод потенциалов — шаг 2
Алгоритм проверки плана на оптимальность и построение цикла пересчета очень подробно расписан в шаге 1.
Далее решение задачи будем излагать менее детально.
Для полученного опорного решения строим вспомогательную — правую таблицу и заполняем значениями из матрицы стоимостей базисные ячейки.
Вычисляем потенциалы строк и столбцов:

Метод потенциалов — шаг 2
По правилу суммирования соответствующих потенциалов, заполняем свободные ячейки.
Вычисляем оценочные значения в свободных ячейках.
Для этого из значений матрицы стоимостей вычитаем найденные значения соответствующих свободных ячеек.
Среди оценочных значений нет отрицательных, следовательно план перевозки оптимален.
Получили оптимальный план. Итоговая стоимость перевозки S1 = 1275

Задание
В городе имеются три домостроительных комбината (ДСК): А1, А2, А3 и строятся четыре микрорайона: В1, В2, В3, В4. Известны ресурсы: А1 – 80, А2 – 130, А3 – 190 и производственные потребности унифицированных изделий микрорайона: В1 – 140, В2 – 100, В3 – 100, В4 – 60. Известны также затраты, связанные с доставкой одного комплекта унифицированных изделий из каждого пункта комплектования в каждый пункт назначения.
Требуется распределить продукцию ДСК по микрорайонам, чтобы суммарные приведенные затраты, связанные с доставкой всего груза от отправителя к потребителю, были минимальны.