Объёмы тел Изображения пространственных фигур Интуитивное, живое пространственное воображение в сочетании со строгой логикой мы
Содержание
- 2. Объёмы тел Изображения пространственных фигур СТЕРЕОМЕТРИЯ
- 3. Интуитивное, живое пространственное воображение в сочетании со строгой логикой мышления — это ключ к изучению стереометрии
- 4. ГЕОМЕТРИЯ возникла из практических задач людей; ГЕОМЕТРИЯ лежит в основе всей техники и большинства изобретений человечества;
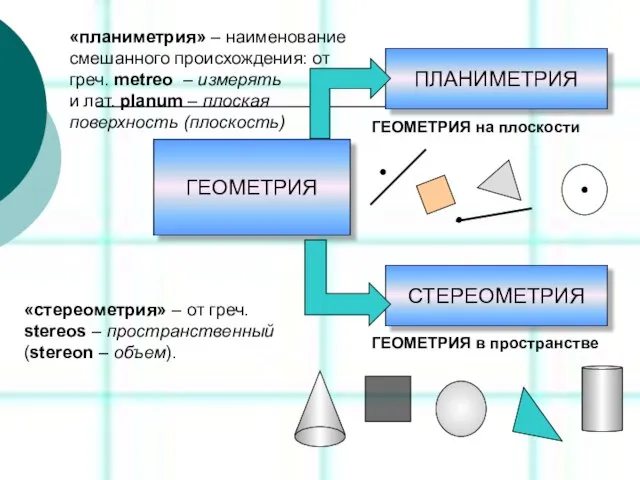
- 5. ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ ГЕОМЕТРИЯ на плоскости ГЕОМЕТРИЯ в пространстве «планиметрия» – наименование смешанного происхождения: от греч. metreo
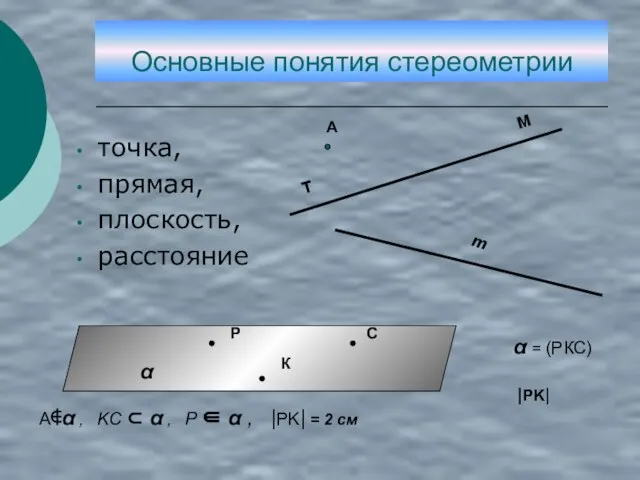
- 6. Основные понятия стереометрии точка, прямая, плоскость, расстояние α = (РКС) |PK| A∉α , KC ⊂ α
- 7. Аксиомы стереометрии Слово «аксиома» греческого происхождения и в переводе означает истинное, исходное положение теории. Понятия «точка»,
- 8. Аксиомы стереометрии А-1 α = (РКС) Через любые три точки, не лежащие на одной прямой проходит
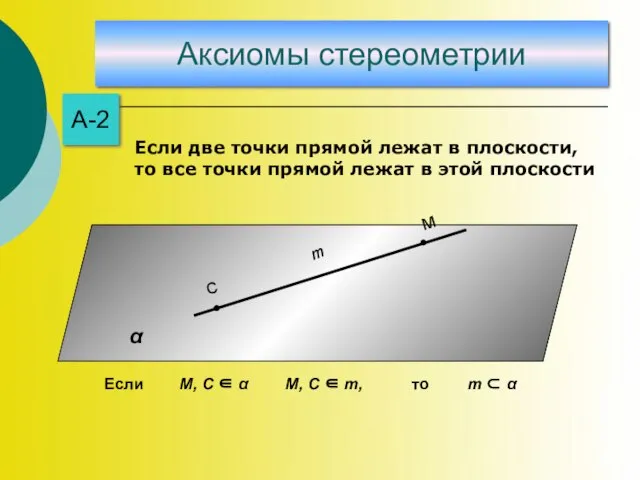
- 9. Аксиомы стереометрии А-2 m М, C ∈ α m ⊂ α М, C ∈ m, Если
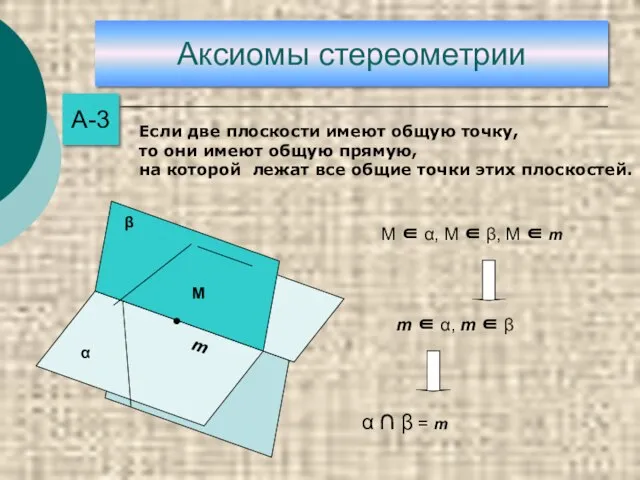
- 10. Аксиомы стереометрии А-3 М ∈ α, М ∈ β, М ∈ m m ∈ α, m
- 11. СЛЕДСТВИЯ ИЗ АКСИОМ Т-1 Через любую прямую и не принадлежащую ей точку можно провести плоскость, и
- 12. СЛЕДСТВИЯ ИЗ АКСИОМ Т-2 Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
- 13. По трем точкам, не лежащим на одной прямой По прямой и точке, не лежащей на этой
- 14. Определение Тело называется простым, если его можно разбить на конечное число треугольных пирамид. В частности, любой
- 15. за единицу объема принят объем куба, ребро которого равно единице длины; если тело разбить на части,
- 16. Теорема 1. Объем прямоугольного параллелепипеда равен произведению его измерений: V = abc Теорема 2. Объем прямой
- 17. Рассмотрим произвольную прямую треугольную призму ABCA1B1C1 Если Δ ABC не прямоугольный, то его можно разбить на
- 18. Рассмотрим произвольную прямую треугольную призму ABCA 1 B 1 C 1 Если Δ ABC не прямоугольный,
- 19. Объем наклонной призмы равен площади перпендикулярного сечения на боковое ребро: V = S пс Пусть ABCA1B1C1
- 20. Объем наклонной призмы равен произведению площади основания на высоту: V = S · H . Пусть
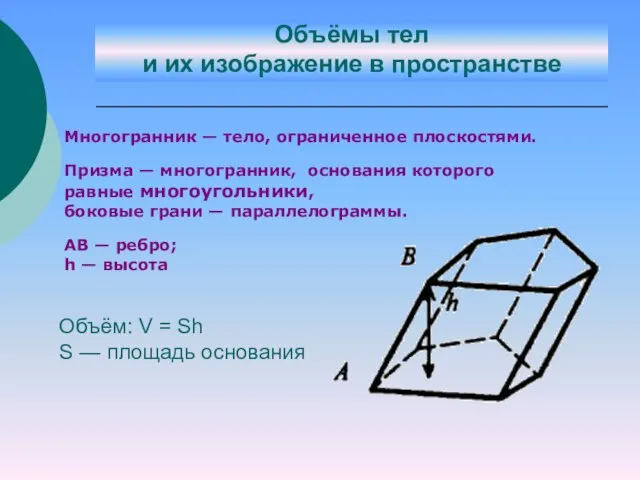
- 21. . Объём: V = Sh S — площадь основания Многогранник — тело, ограниченное плоскостями. Призма —
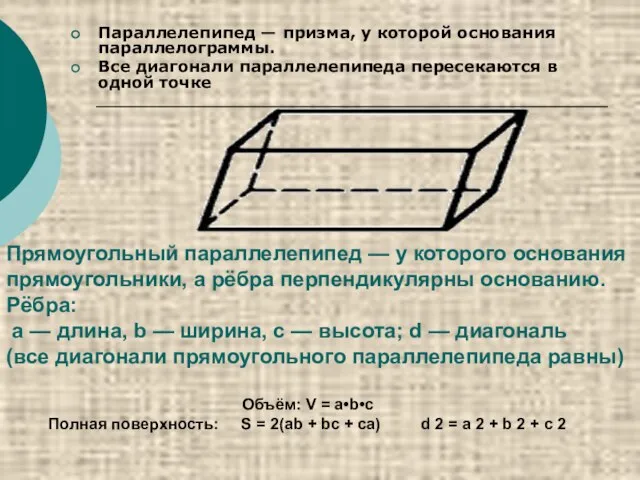
- 22. Параллелепипед — призма, у которой основания параллелограммы. Все диагонали параллелепипеда пересекаются в одной точке Прямоугольный параллелепипед
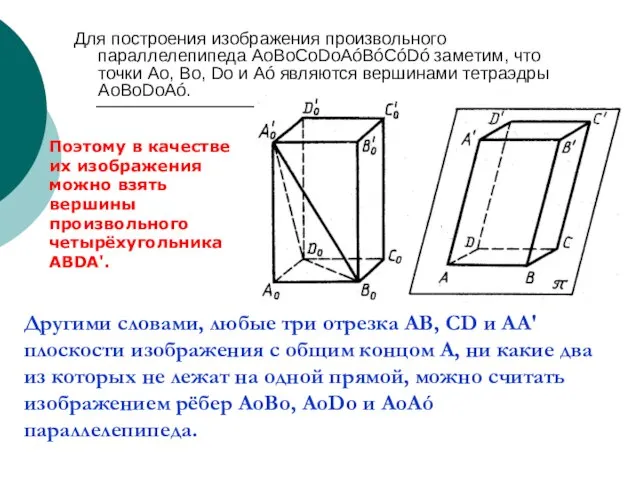
- 23. Для построения изображения произвольного параллелепипеда AоBоCоDоAóBóСóDó заметим, что точки Ао, Во, Dо и Аó являются вершинами
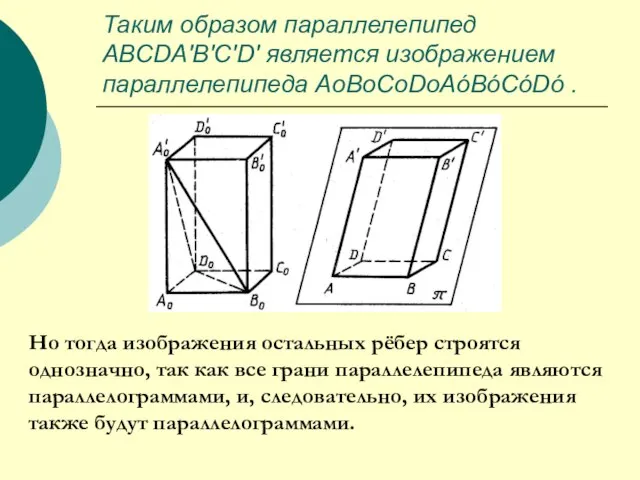
- 24. Таким образом параллелепипед ABCDA'B'C'D' является изображением параллелепипеда AоBоCоDоAóBóСóDó . Но тогда изображения остальных рёбер строятся однозначно,
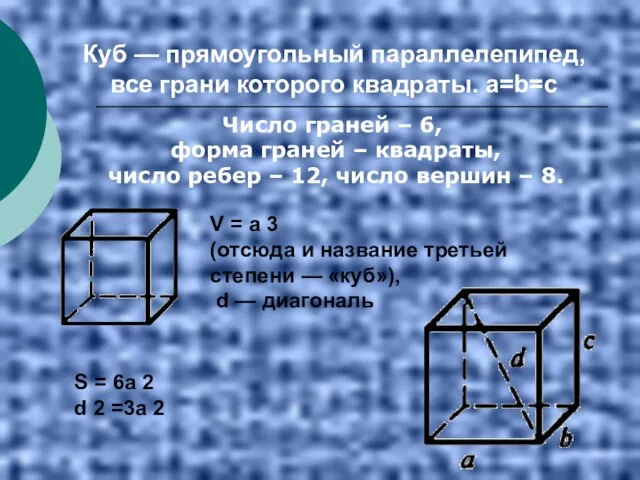
- 25. Куб — прямоугольный параллелепипед, все грани которого квадраты. а=b=с V = а 3 (отсюда и название
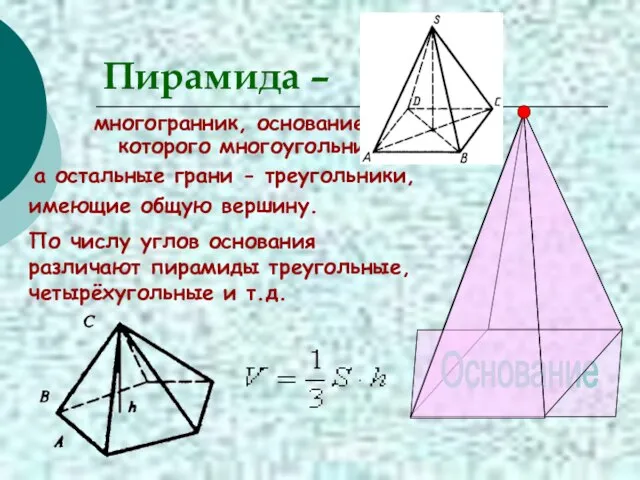
- 26. Пирамида – многогранник, основание которого многоугольник, а остальные грани - треугольники, имеющие общую вершину. По числу
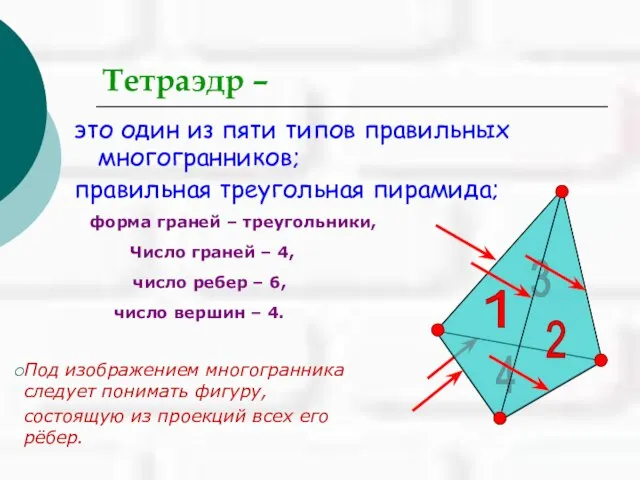
- 27. 4 3 Тетраэдр – это один из пяти типов правильных многогранников; правильная треугольная пирамида; 1 2
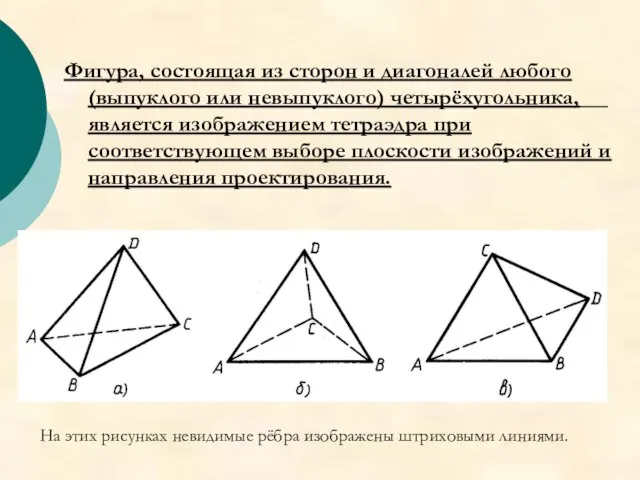
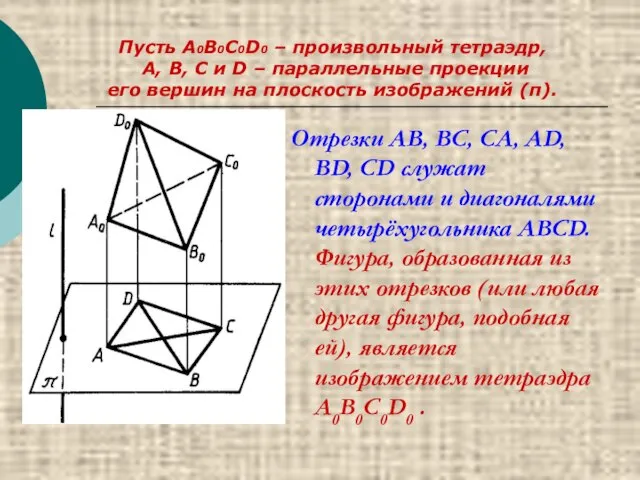
- 28. Фигура, состоящая из сторон и диагоналей любого (выпуклого или невыпуклого) четырёхугольника, является изображением тетраэдра при соответствующем
- 29. Отрезки AB, BC, CA, AD, BD, CD служат сторонами и диагоналями четырёхугольника ABCD. Фигура, образованная из
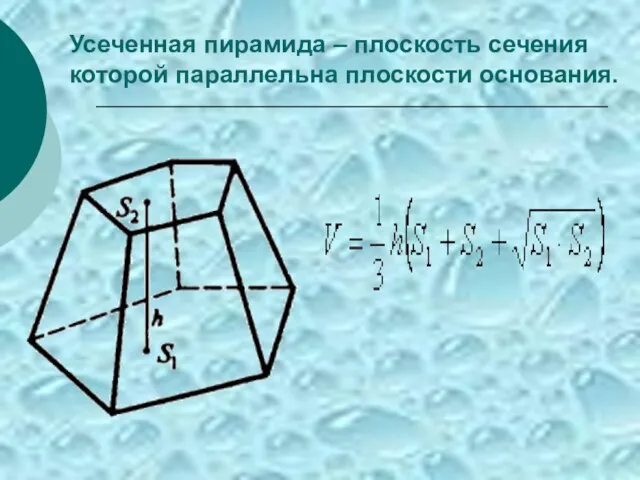
- 30. Усеченная пирамида – плоскость сечения которой параллельна плоскости основания.
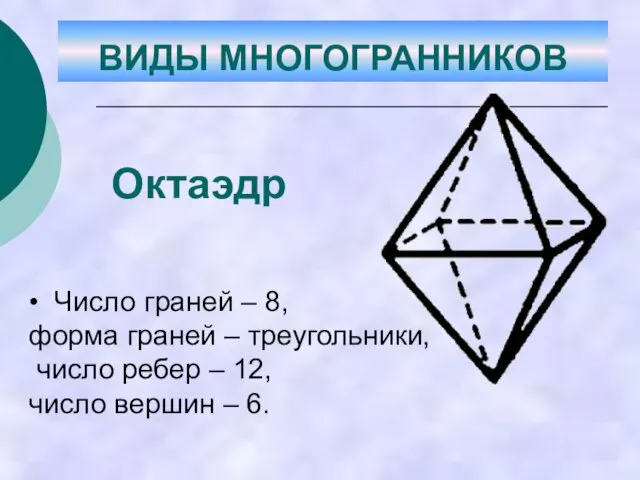
- 31. • Число граней – 8, форма граней – треугольники, число ребер – 12, число вершин –
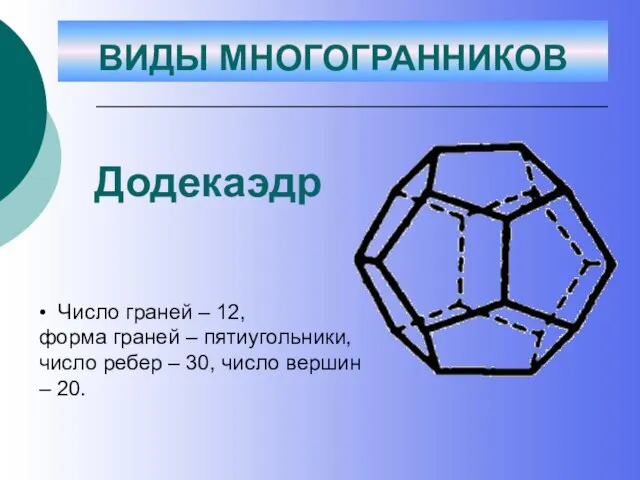
- 32. Додекаэдр • Число граней – 12, форма граней – пятиугольники, число ребер – 30, число вершин
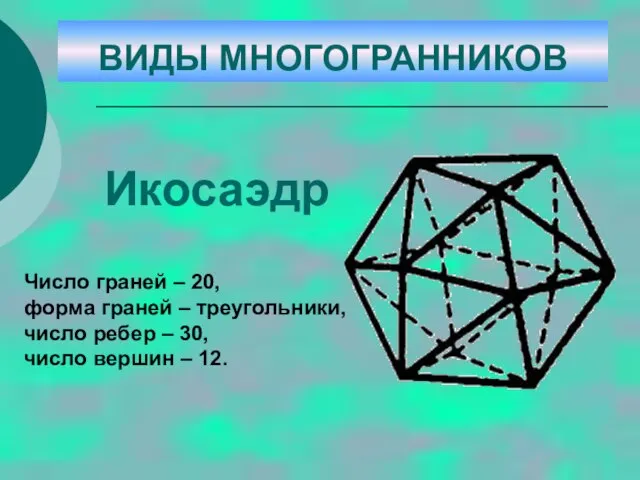
- 33. Икосаэдр Число граней – 20, форма граней – треугольники, число ребер – 30, число вершин –
- 34. Цилиндры. • Круглый прямой. • Круглый усеченный S – площадь боковой поверхности. V – объем. ТЕЛА
- 35. Сфера – поверхность шара ТЕЛА ВРАЩЕНИЯ
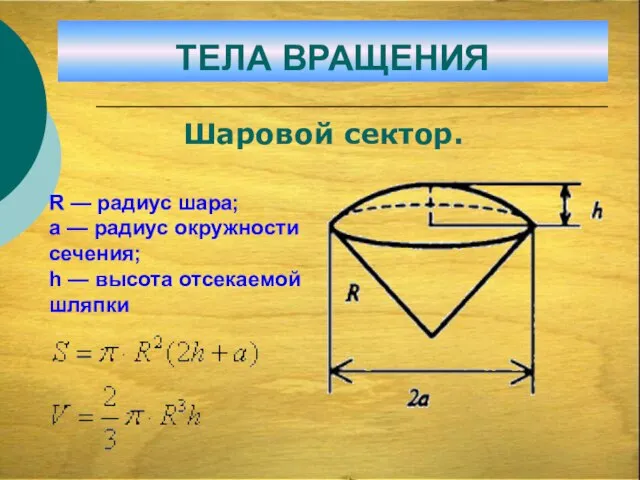
- 36. R — радиус шара; а — радиус окружности сечения; h — высота отсекаемой шляпки ТЕЛА ВРАЩЕНИЯ
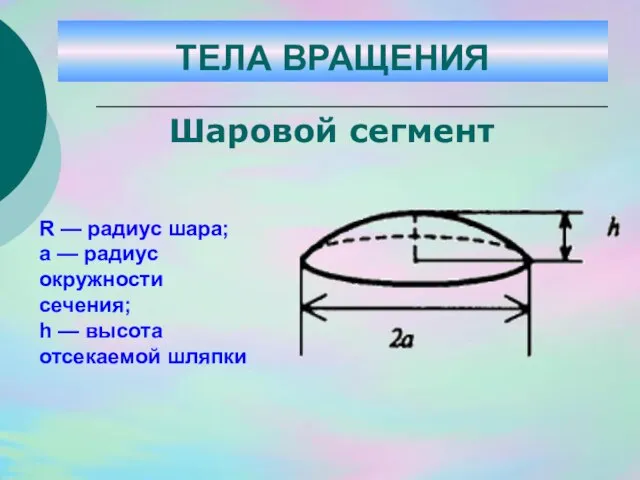
- 37. R — радиус шара; а — радиус окружности сечения; h — высота отсекаемой шляпки Шаровой сегмент
- 38. R — радиус шара, a , b — радиусы окружностей сечений, h — высота слоя Шаровой
- 39. Сюда входит: выбор оптимального положения изображаемого тела (в частности, выбор ориентации - верх и низ, право
- 41. Скачать презентацию



















 Итоговый урок физика8 класс
Итоговый урок физика8 класс Кто знает обо всём
Кто знает обо всём Дизайн как вид изобразительного искусства
Дизайн как вид изобразительного искусства Разработка домашнего задания на тему: матрешка
Разработка домашнего задания на тему: матрешка Аймактардын социалдык-экономикалык ?н?г?? тенденциясы
Аймактардын социалдык-экономикалык ?н?г?? тенденциясы Программа модернизации системы среднего профессионального образования Республики Карелия
Программа модернизации системы среднего профессионального образования Республики Карелия Ну-ка, проверь-ка, дружок, Ты готов начать урок? Всё ль на месте, всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Вс
Ну-ка, проверь-ка, дружок, Ты готов начать урок? Всё ль на месте, всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Вс HTML Первые шаги.
HTML Первые шаги. Формы сохранения культурного наследия
Формы сохранения культурного наследия Выбирай банк смолоду: предложение Райффайзенбанка для молодёжи от команды Giants
Выбирай банк смолоду: предложение Райффайзенбанка для молодёжи от команды Giants Месяц тотального рекрутинга. Только в апреле каждому новичку КЭШБЭК 10%
Месяц тотального рекрутинга. Только в апреле каждому новичку КЭШБЭК 10% Типичные задачи по математике
Типичные задачи по математике Анимация кроссвордовколлективное творчество участников сообщества "ИКТ в НШ"
Анимация кроссвордовколлективное творчество участников сообщества "ИКТ в НШ"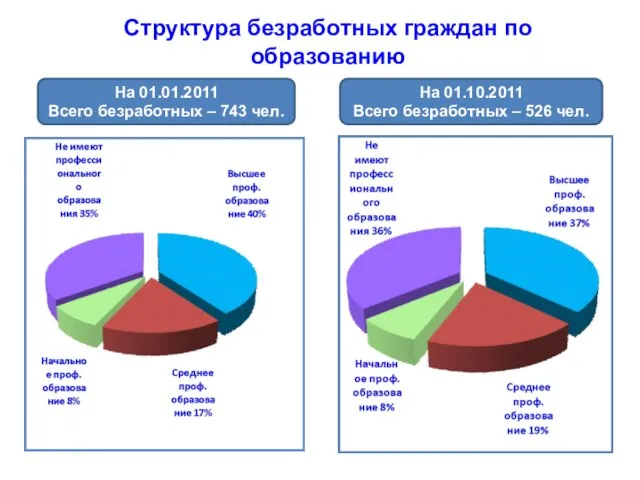 Структура безработных граждан по образованию
Структура безработных граждан по образованию Дистанционный Кадавер курс
Дистанционный Кадавер курс Оценка безопасности комбинации индометацина и тиотриазолина по влиянию на слизистую желудка
Оценка безопасности комбинации индометацина и тиотриазолина по влиянию на слизистую желудка Линии одним росчерком пера
Линии одним росчерком пера Political System of Kazakhstan
Political System of Kazakhstan  Семья Яковлевых прдставляет
Семья Яковлевых прдставляет История расчески
История расчески Какими средствами воздействует искусство? 7 класс
Какими средствами воздействует искусство? 7 класс Физика и искусство
Физика и искусство Как общаться с подростком
Как общаться с подростком Как посвятить учеников в ряды пятиклассников
Как посвятить учеников в ряды пятиклассников 20140928_dimova_v.m.priem_rabota_s_risunkami._tektonicheskaya_karta
20140928_dimova_v.m.priem_rabota_s_risunkami._tektonicheskaya_karta Роберт Шуман
Роберт Шуман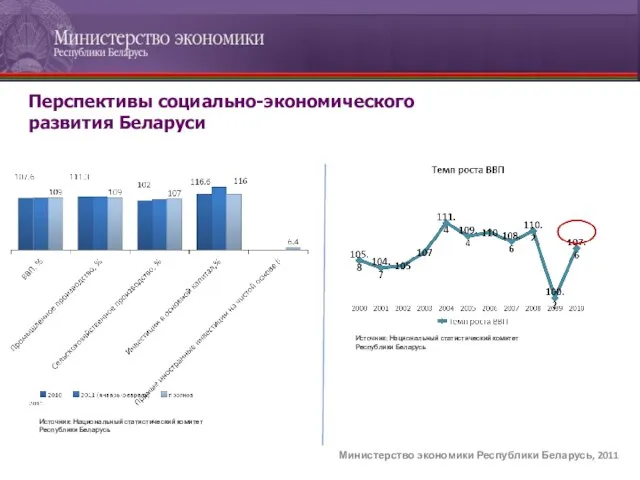 Перспективы социально-экономического развития Беларуси
Перспективы социально-экономического развития Беларуси Презентация на тему Правовой статус таможенного перевозчика
Презентация на тему Правовой статус таможенного перевозчика