Радиоавтоматика. Лекция 14

ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА ДИСКРЕТНОЙ СИСТЕМЫ
Перейти к оригиналу можно, разложив изображение H(z) в ряд Лорана H(z) = h0 + h1z -1 + h2z -2 +…
решением разностного уравнения системы при x[n] = 1[n],
вычислением изображения переходной характеристики H(z) = Z{1[n]}K(z) с последующим переходом к оригиналу.
Сравнивая этот ряд с Z-преобразованием переходной характеристики
Найти переходную характеристику можно:
видим, что h[0] = h0, h[1] = h1, h[2] = h2 и т.д.
Выясним связь формы переходной характеристики с положением корней на комплексной плоскости Z
Если корень (z1) находится на действительной оси, тогда свободная составляющая yсв[n] = Az1n и переходная характеристика h[n] = 1 – z1n.

Для положительного корня (0 < z1 ≤ 1) переходная характеристика монотонная, а для отрицательного корня (-1 ≤ z1 < 0) колебательная с периодом колебаний, равным двум интервалам дискретизации.
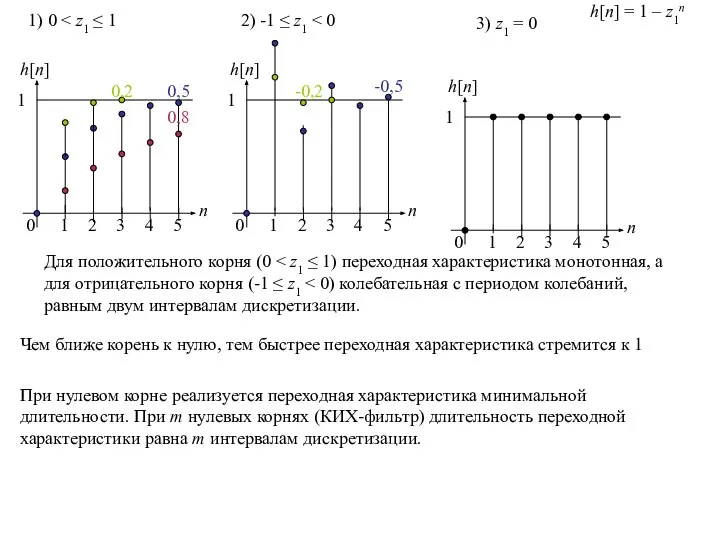
1) 0 < z1 ≤ 1
2) -1 ≤ z1 < 0
3) z1 = 0
При нулевом корне реализуется переходная характеристика минимальной длительности. При m нулевых корнях (КИХ-фильтр) длительность переходной характеристики равна m интервалам дискретизации.
h[n] = 1 – z1n
Чем ближе корень к нулю, тем быстрее переходная характеристика стремится к 1

4) Два комплексно – сопряженных корня
h[n] = 1 – 0,5(z1n + z2n) =
1 – 0,5| z1 |n (e jnArg(z1) – e -jnArg(z1)) =
= 1 – 0,5| z1 |n 2cos(nArg(z1)) = 1 –| z1 |n cos(nArg(z1)).
Пример: z1,2 = 0,5e± j π/2
Переходная характеристика колебательная с периодом колебаний на вершине, равным целому от 2π/Arg(z1).
Чем ближе корни к окружности, тем больше амплитуда колебаний и медленней затухание.
Чем ,ближе корни к 1, тем больше период колебаний на вершине переходной характеристики и больше время регулирования.
h[n]=1-0,5ncos(nπ/2)

ОШИБКИ РЕГУЛИРОВАНИЯ
Функциональная схема для расчета ошибок в следящей системе:
Изображение ошибки:
Δ(z) = Xз(z) – Y(z) = Xз(z) – {Xз(z) + Xв(z)}Kз(z) =
{1 – Kз(z)} Xз(z) –Kз(z) Xв(z)
Динамическая ошибка
Ошибка по возмущению
1) Динамическая ошибка при полиномиальном задающем воздействии.
Δдин (z) = {1 – Kз(z)} Xз(z) = Kош(z) Xз(z).
Перейдем к оригиналу, разложив передаточную функцию ошибки в ряд по оператору разности.
Найдем этот оператор: Z{Δx[n]} = Z{x[n + 1] – x[n] } =
z X(z) – X(z) = (z – 1) X(z).
z – 1 – оператор разности.

Kош(z) = S0 + S1(z – 1) + S2(z – 1)2 + … ,
где S0 = Kош(z = 1),
Δдин(z) =[ S0 + S1(z – 1) + S2(z – 1)2 + …]Xз(z) ,
δдин[n] = S0xз[n] + S1Δxз[n] + S2Δ2xз[n] + …,
а) Статическая ошибка (при xз[n] =x0)
Δ xз[n] = xз[n + 1] – xз[n] = x0 – x0 = 0
δст[n] = S0x0.
б) Скоростная ошибка (при xз[n] =Δx0n ),
где Δx0 – приращение входного процесса за интервал дискретизации.
Δ xз[n] = xз[n + 1] – xз[n] = Δx0(n + 1) – Δx0n = Δx0.
Δ2 xз[n] = Δxз[n + 1] – Δ xз[n] = Δx0 – Δx0 = 0.
δуск[n] = S0 (Δ2x0/2) n2 + S1 (Δ2x0/2) (2n + 1) + S2 Δ2x0.
в) Ошибка по ускорению (при xз[n] = (Δ2x0/2) n2 ),
Δ xз[n] = (Δ2x0/2) (n + 1)2 – (Δ2x0/2) n2 = (Δ2x0/2) (2n + 1).
Δ2xз[n] = Δxз[n + 1] – Δxз[n] = (Δ2x0/2) (2(n + 1) + 1) – (Δ2x0/2) (2n + 1) = Δ2x0.
Δ3xз[n] = Δ2xз[n + 1] – Δ2xз[n] = Δ2x0 – Δ2x0 = 0.
δск[n] = S0 Δx0n + S1Δx0.