Системы счисления

Что такое система счисления?
Система счисления – это способ наименования и обозначения чисел.

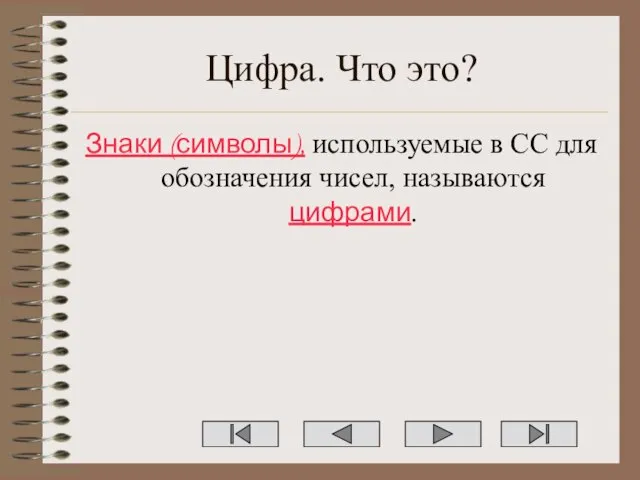
Цифра. Что это?
Знаки (символы), используемые в СС для обозначения чисел, называются цифрами.

Римская система счисления
Не является позиционной, т.е. каждый символ обозначает всегда одно и тоже число;
Цифры обозначаются латинскими буквами:
I, V, X, L, C, D, M
(1, 5, 10, 50, 100, 500, 1000)
Например: XXX – 30; XLI - 41

Позиционные системы счисления
Основанием системы может быть любое натуральное число, большее единицы;
Основание ПСС – это количество цифр, используемое для представления чисел;
Значение цифры зависит от ее позиции, т.е. одна и та же цифра соответствует разным значениям в зависимости от того, в какой позиции числа она стоит;
Например: 888: 800; 80; 8
Любое позиционное число можно представить в виде суммы степеней основания системы.

Десятичная СС
Основание системы – число 10;
Содержит 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
Любое десятичное число можно представить в виде суммы степеней числа 10 – основания системы;

Двоичная СС
Основание системы – 2;
Содержит 2 цифры: 0; 1;
Любое двоичное число можно представить в виде суммы степеней числа 2 – основания системы;
Примеры двоичных чисел: 11100101; 10101;

Правила перехода
Из десятичной СС в двоичную СС:
Разделить десятичное число на 2. Получится частное и остаток.
Частное опять разделить на 2. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим 2.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет двоичной записью исходного десятичного числа.

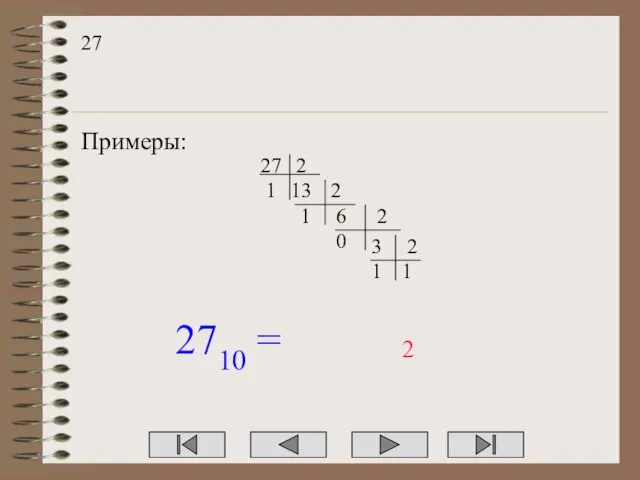
27
Примеры:
27
2
13
1
2
6
1
2
3
0
2
1
1
2710 =
2

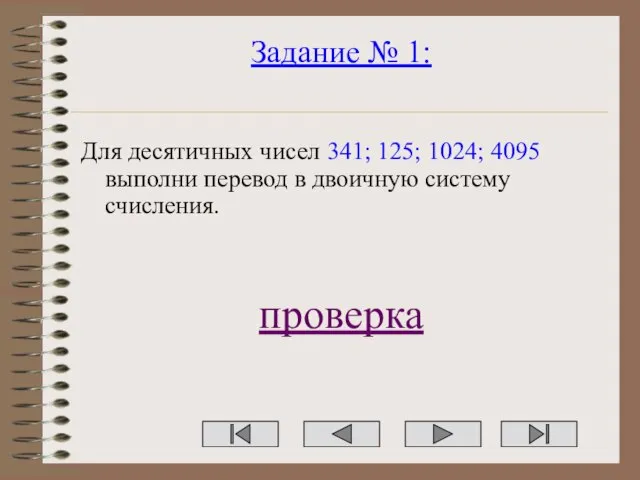
Задание № 1:
Для десятичных чисел 341; 125; 1024; 4095 выполни перевод в двоичную систему счисления.
проверка

2. Правило перехода из двоичной системы счисления в десятичную.
Для перехода из двоичной системы счисления в десятичную необходимо двоичное число представить в виде суммы степеней двойки и найти ее десятичное значение.
Пример:
111012 =
1*2 4 +
1*2 3+
1*2 2 +
0*2 1 +
1*2 0 =
= 16 +
8 +
4 +
0 +
1 =
2910

Задание № 2:
Двоичные числа 1011001, 11110, 11011011 перевести в десятичную систему.
проверка

Восьмеричная СС
Основание системы – 8;
Содержит 8 цифр: 0; 1; 2; 3; 4; 5; 6; 7;
Любое восьмеричное число можно представить в виде суммы степеней числа 8 – основания системы;
Примеры восьмеричных чисел: 2105; 73461;

Правило перехода из десятичной системы счисления в восьмеричную
Разделить десятичное число на 8. Получится частное и остаток.
Частное опять разделить на 8. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим 8.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет восьмеричной записью исходного десятичного числа.

Примеры:
132
8
16
4
8
2
0
13210 =
8

Задание № 3:
Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему.
проверка

Правило перехода из восьмеричной системы счисления в десятичную.
Для перехода из восьмеричной системы счисления в десятичную необходимо восьмеричное число представить в виде суммы степеней восьмерки и найти ее десятичное значение.
2158 =
2*82 +
1*81+
5*80 =
= 128 +
8 +
5 =
14110

Задание № 4:
Восьмеричные числа 41, 520, 306 перевести в десятичную систему.
проверка

Шестнадцатеричная СС
Основание системы – 16;
Содержит 16 цифр: от 0 до 9; A; B; C; D; E; F;
Любое шестнадцатеричное число можно представить в виде суммы степеней числа 16 – основания системы;
Примеры шестнадцатеричных чисел: 21AF3; B09D;

Правило перехода из десятичной системы счисления в шестнадцатеричную
Разделить десятичное число на 16. Получится частное и остаток.
Частное опять разделить на 16. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим 16.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет шестнадцатеричной записью исходного десятичного числа.

Примеры:
335
16
20
1
16
1
4
33510 =
16
5
F

Задание № 5:
Десятичные числа 512, 302, 2045 перевести в шестнадцатеричную систему.
проверка

Правило перехода из шестнадцатеричной системы счисления в десятичную.
Для перехода из шестнадцатеричной системы счисления в десятичную необходимо шестнадцатеричное число представить в виде суммы степеней шестнадцати и найти ее десятичное значение.
A1416 =
10*162 +
1*161 +
4*160 =
= 10*256 +
16 +
4 =
258010

Задание № 6:
Шестнадцатеричные числа B5, A28,CD перевести в десятичную систему.
проверка

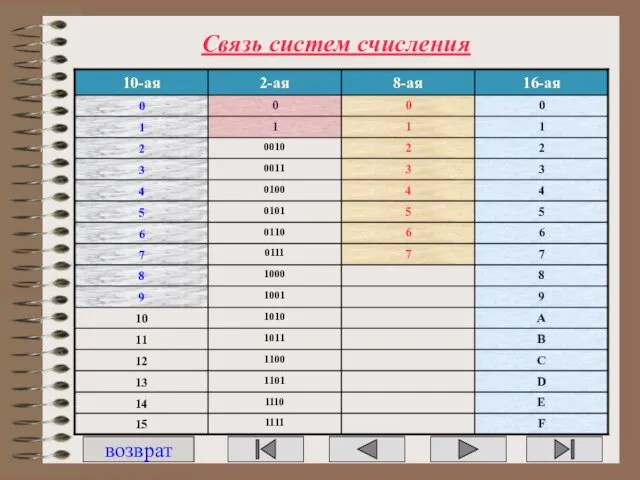
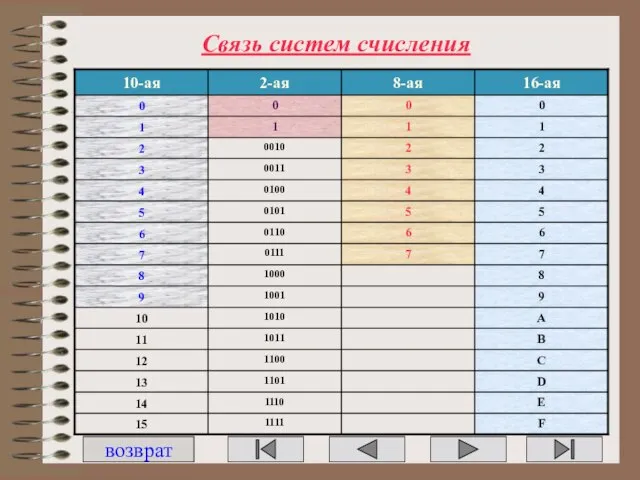
Связь систем счисления
возврат

Правило перехода из двоичной системы счисления в восьмеричную
Разбить двоичное число на классы справа налево по три цифры в каждом. Заменить каждый класс соответствующей восьмеричной цифрой.
1
1
1
0
1
1
0
0
1
0
2
=
1
6
5
4
8

Задание № 7:
Двоичные числа 10101111, 11001100110 перевести в восьмеричную систему
проверка

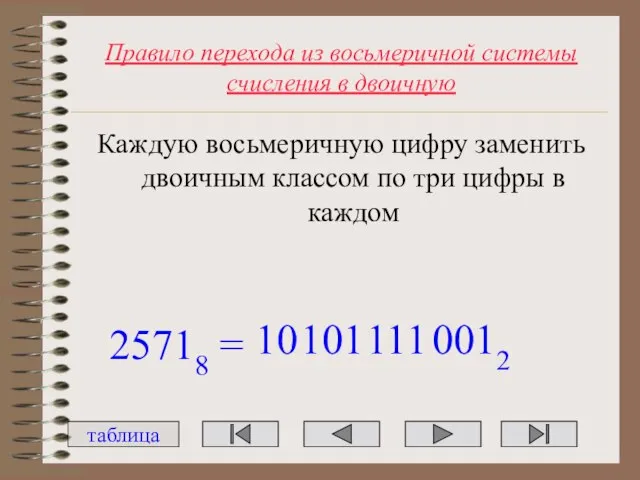
Правило перехода из восьмеричной системы счисления в двоичную
Каждую восьмеричную цифру заменить двоичным классом по три цифры в каждом
25718 =
10
101
111
0012
таблица

Задание № 8:
Восьмеричные числа 26, 702, 4017 перевести в двоичную систему.
проверка

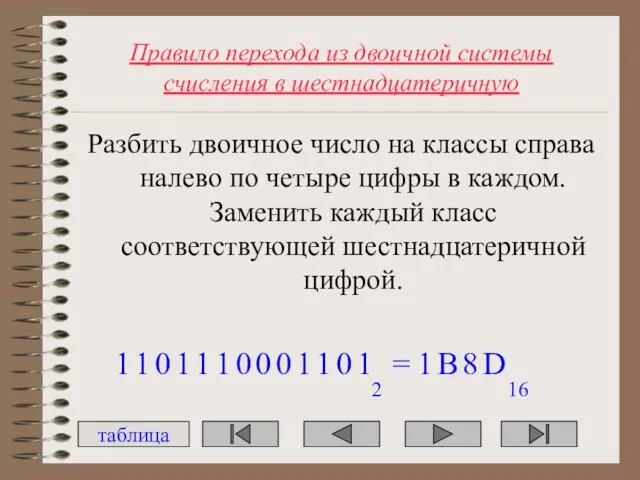
Правило перехода из двоичной системы счисления в шестнадцатеричную
Разбить двоичное число на классы справа налево по четыре цифры в каждом. Заменить каждый класс соответствующей шестнадцатеричной цифрой.
1
1
0
1
1
0
1
0
0
1
2
1
0
1
=
1
B
8
D
16
таблица

Задание № 9:
Двоичные числа 10101111, 11001100110 перевести в шестнадцатеричную систему
проверка

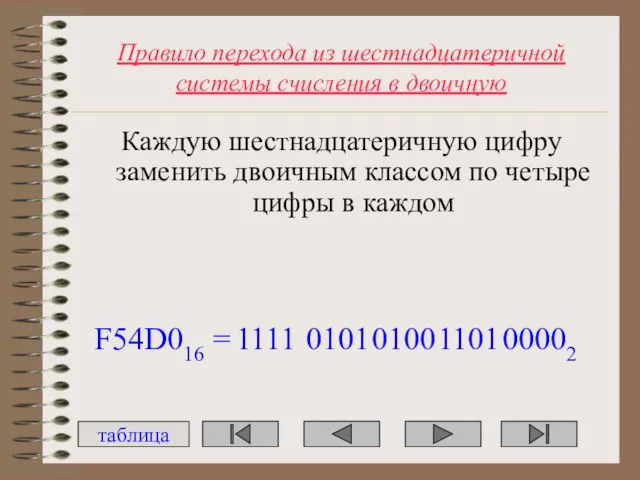
Правило перехода из шестнадцатеричной системы счисления в двоичную
Каждую шестнадцатеричную цифру заменить двоичным классом по четыре цифры в каждом
таблица
F54D016 =
0101
0100
1101
00002
1111

Задание № 10:
Шестнадцатеричные числа C3, B096, E38 перевести в двоичную систему.
проверка

Задания для домашней работы
Для каждого из чисел: 12310, 45610 выполнить перевод: 10→2, 10 → 8, 10 → 16.
Для каждого из чисел: 1000112, 1010010112, 11100100012 выполнить перевод: 2 → 10, 2 → 8, 2 → 16.
Для чисел: 543218, 545258, 7778, 1AB16, A1B16, E2E416, E7E516 выполнить соответствующий перевод: 8 → 2, 16 → 2.

Ответы к заданию №1

Ответы к заданию № 2

Ответы к заданию №3

Ответы к заданию №4

Ответы к заданию №5

Ответы к заданию №6

Ответы к заданию №7

Ответы к заданию №8

Ответы к заданию №9

Ответы к заданию №10

Связь систем счисления
возврат