Содержание
- 2. С 2005/2006 года итоговая аттестация (ГИА) по алгебре проходит в новой форме, которая, несмотря на очевидную
- 3. Первая часть предусматривает выполнение тестовых заданий . При этом ответы заданий фиксируются учениками непосредственно на бланке
- 4. Вторая часть имеет вид традиционной контрольной работы и состоит из пяти заданий, в которых в соответствии
- 5. Литература для подготовки к экзамену.
- 6. Решение задач с параметром аналитически
- 7. 1. Найдите значение p при которых парабола касается оси х. Для каждого значения p определите координаты
- 8. 2. Найдите все значения а, при которых , неравенство не имеет решений. Решение и ответ График
- 9. 3. Прямая касается окружности в точке с положительной абсциссой. Определите координаты точки касания. Решение и ответ
- 10. Решение и ответ 2) Полученное уравнение имеет единственное решение, когда его дискриминант равен нулю. Имеем: Решив
- 11. 4. Парабола проходит через точки А(0;-4), В(-1; -11), С(4;4). Найдите координаты ее вершины. Решение и ответ
- 12. Решаем систему Решение и ответ Отсюда: а=-1, b=6.Уравнение параболы имеет вид 2) Найдем координаты вершины:
- 13. 5. При каких значениях m уравнение имеет два различных корня? Решение и ответ Представим уравнение в
- 14. Решение и ответ При получаем полное квадратное уравнение. Если его дискриминант равен нулю, то оно имеет
- 15. 6. При каких значениях m и n, связанных соотношением m+n=2, выражение принимает наименьшее значение? Решение и
- 16. 7Найдите все отрицательные значения m, при которых система уравнений не имеет решений. Решение и ответ Подставим
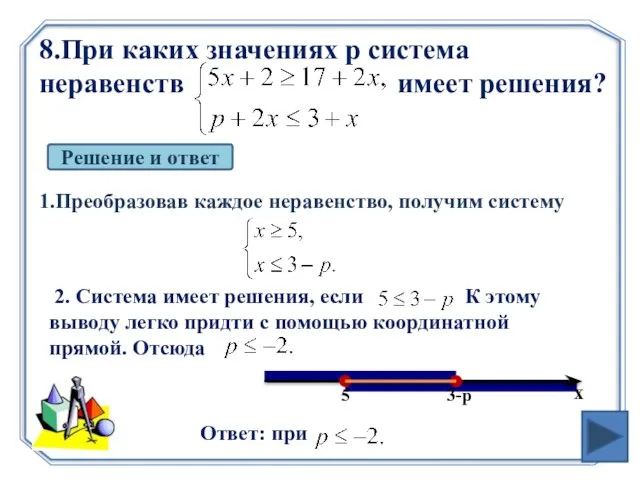
- 17. 8.При каких значениях p система неравенств имеет решения? Решение и ответ 1.Преобразовав каждое неравенство, получим систему
- 18. 9.При каких значениях n решением неравенства является любое число? Решение и ответ 1.Так как ветви параболы
- 19. 10.При каких отрицательных значениях k прямая y=kx-4 пересекает параболу в двух точках? Решение и ответ 1.Прямая
- 20. Решение задач с параметром графически
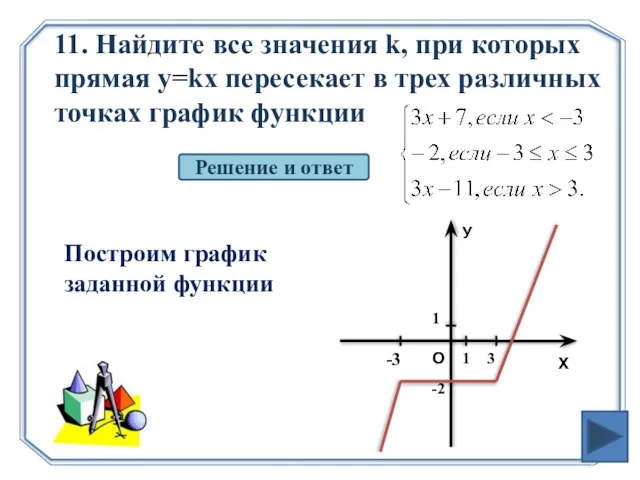
- 21. 11. Найдите все значения k, при которых прямая y=kx пересекает в трех различных точках график функции
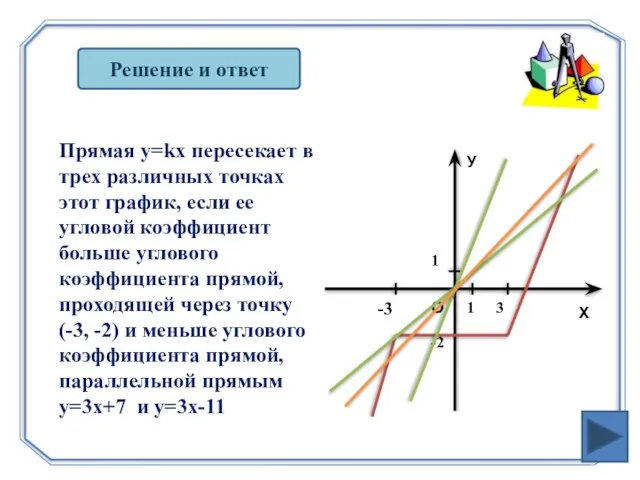
- 22. Решение и ответ Прямая y=kx пересекает в трех различных точках этот график, если ее угловой коэффициент
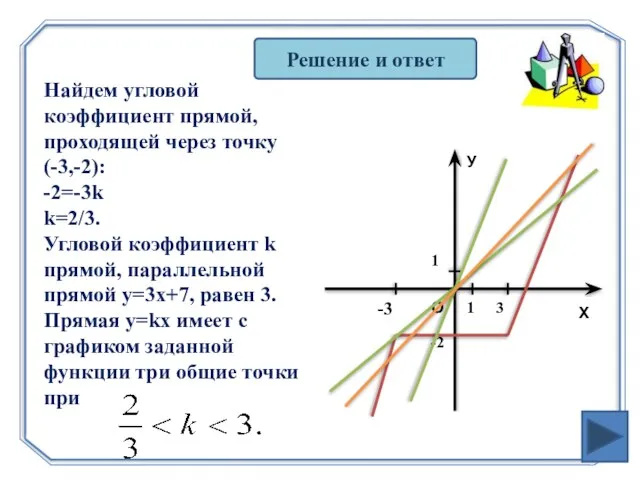
- 23. Решение и ответ Найдем угловой коэффициент прямой, проходящей через точку (-3,-2): -2=-3k k=2/3. Угловой коэффициент k
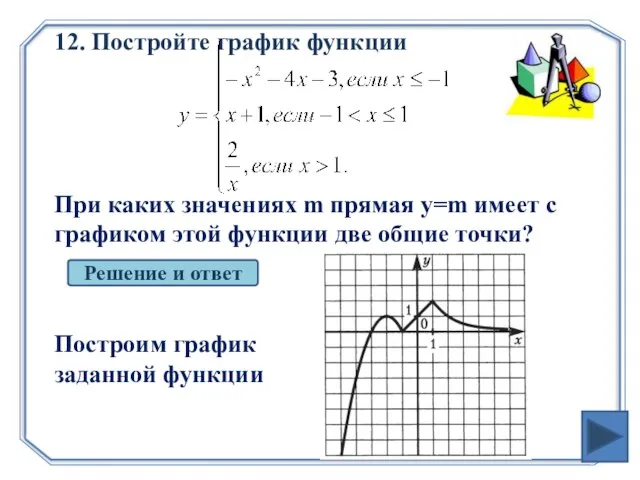
- 24. 12. Постройте график функции При каких значениях m прямая y=m имеет с графиком этой функции две
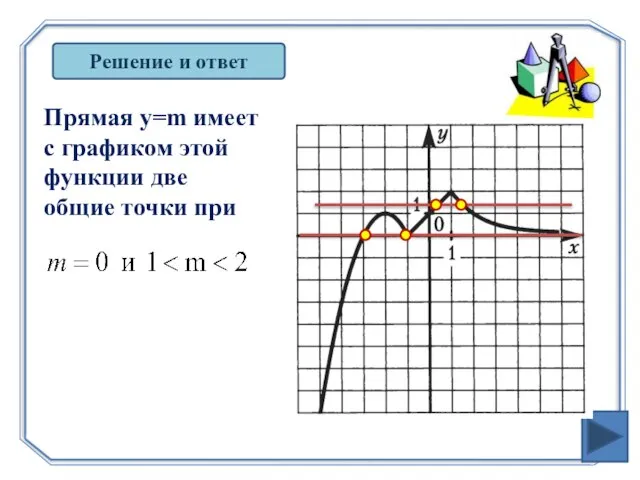
- 25. Решение и ответ Прямая y=m имеет с графиком этой функции две общие точки при
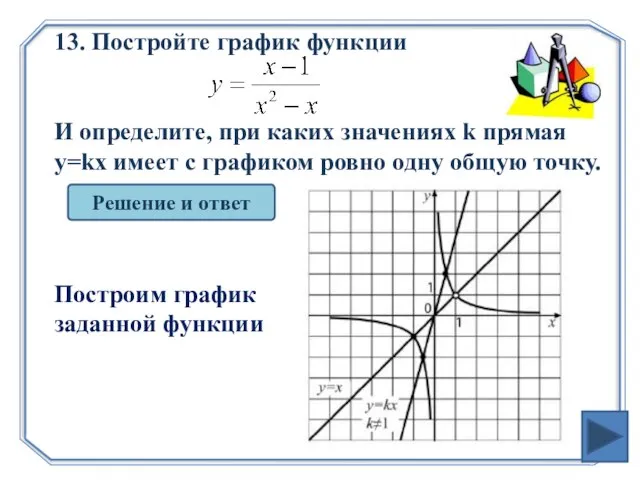
- 26. 13. Постройте график функции И определите, при каких значениях k прямая y=kx имеет с графиком ровно
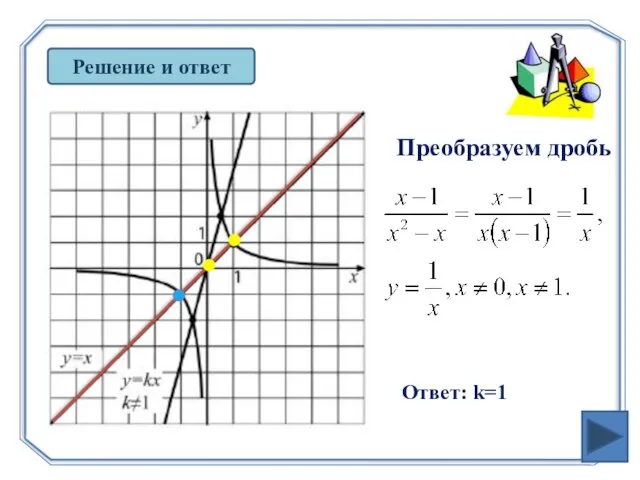
- 27. Решение и ответ Преобразуем дробь Ответ: k=1
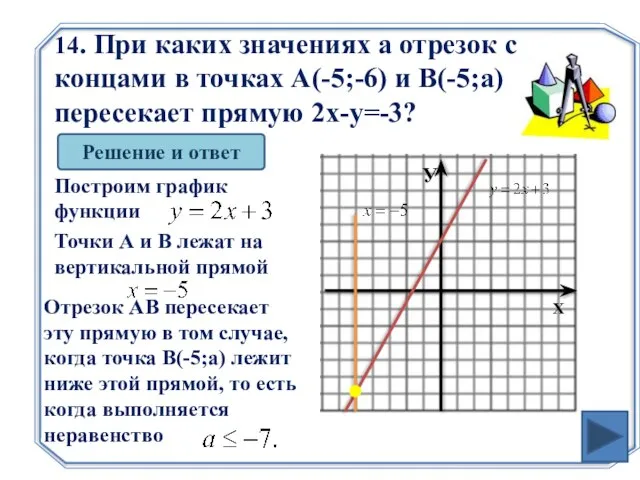
- 28. 14. При каких значениях а отрезок с концами в точках А(-5;-6) и B(-5;а) пересекает прямую 2х-у=-3?
- 30. Скачать презентацию


















 Отдельные виды договорных отношений в жилищном праве
Отдельные виды договорных отношений в жилищном праве Организация велостоянки для гимназии №1
Организация велостоянки для гимназии №1 О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го
О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го Урок русского языка в 6 классе по теме: «Правописание сложных существительных»
Урок русского языка в 6 классе по теме: «Правописание сложных существительных» Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании
Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании Невидимые нити в весеннем лесу (2 класс)
Невидимые нити в весеннем лесу (2 класс) Игрушки из носочков своими руками №7
Игрушки из носочков своими руками №7 Введение в специальность
Введение в специальность Герцог Ами
Герцог Ами Трение. Вредно или полезно
Трение. Вредно или полезно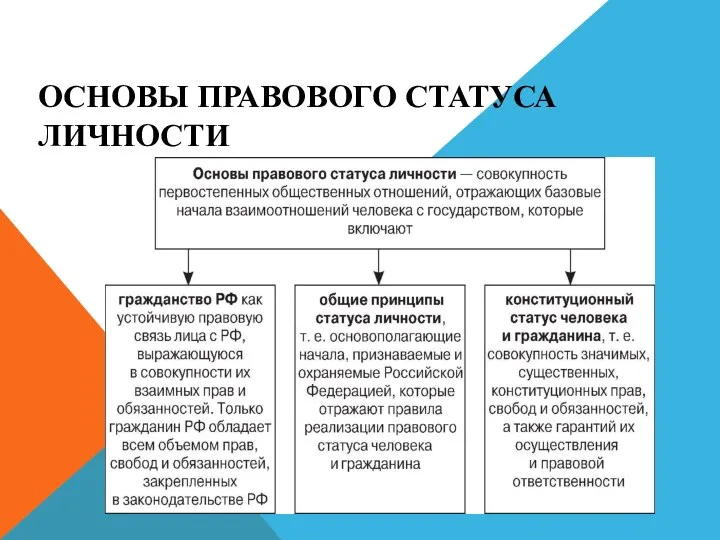 Правовой статус личности. Гражданство РФ
Правовой статус личности. Гражданство РФ Социальная психология
Социальная психология Презентация на тему АФАНАСИЙ НИКИТИН
Презентация на тему АФАНАСИЙ НИКИТИН  Теория обучения
Теория обучения Презентация на тему Our Environment (Наша окружающая среда)
Презентация на тему Our Environment (Наша окружающая среда) Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС)
Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС) Презентация по информатике на тему: «Устройства вывода информации, монитор.»
Презентация по информатике на тему: «Устройства вывода информации, монитор.» Круглопольское сельское поселение
Круглопольское сельское поселение Прайс косметологических услуг салона Забота о вас
Прайс косметологических услуг салона Забота о вас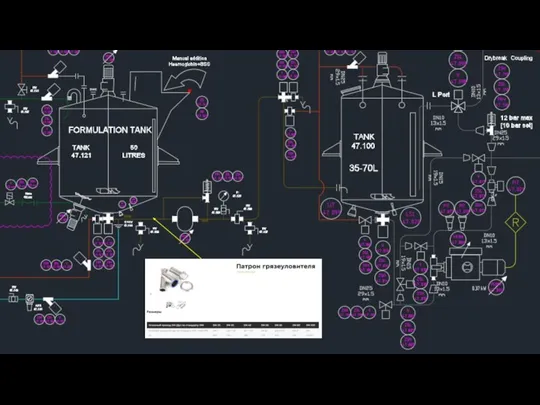 Патрон грязеуловителя
Патрон грязеуловителя Назначение изделия и его описание
Назначение изделия и его описание Планирование и организация процесса закупок материальных ресурсов промышленного предприятия
Планирование и организация процесса закупок материальных ресурсов промышленного предприятия Распространение объектно-ориентированного подхода на информационную безопасность
Распространение объектно-ориентированного подхода на информационную безопасность Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк.
Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк. Пейзаж в графике
Пейзаж в графике Рогожка. Коллекция однотонных штор
Рогожка. Коллекция однотонных штор _Презентация. Предоставление
_Презентация. Предоставление Презентация
Презентация