Conditional statements. Converse and inverse theorem. Types of proofs. Mathematical induction. Sequences. Lecture 2
Содержание
- 2. Conditional statements.
- 3. Let’s train the brain! If student pass exams then he will receive the scholarships. Compound statement:
- 4. Theorem. Inverse and converse theorem. Example 2.1 Theorem. If student pass exams then he will receive
- 5. Let’s train the brain! Theorem. If it rains then the ground is wet. Formulate a) converse
- 6. Types of proofs. Theorem. If a=0 or b=0 then ab=0.
- 7. Mathematical induction
- 9. Example 2.4 Prove that any sum equal or greater than 8 cents may be collected using
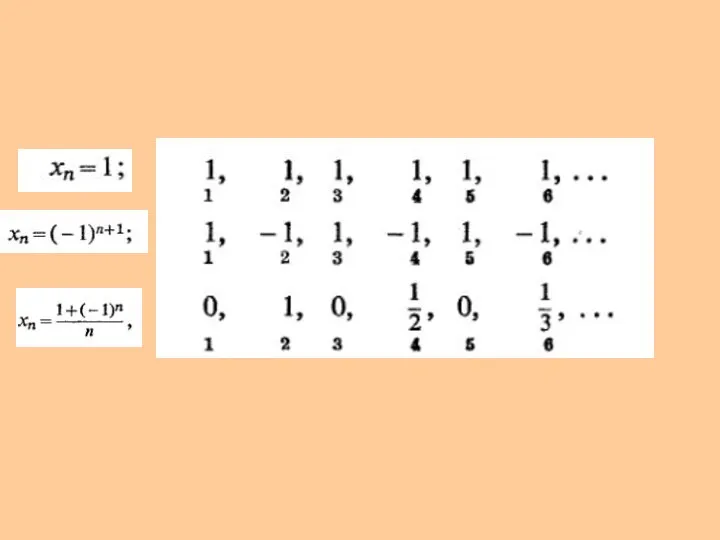
- 10. 2.1 Sequences of real numbers
- 11. Examples of sequences Arithmetic progression 2) Geometric progression 3) Approximation to π
- 16. Скачать презентацию












 Формы глагола
Формы глагола ВПР. Английский язык
ВПР. Английский язык Food and drink
Food and drink Build and figure
Build and figure Welcome to the cafe
Welcome to the cafe CAN or MAY
CAN or MAY Can. Английский язык
Can. Английский язык Force and Motion
Force and Motion Жизнь Эмилии Эрхарт
Жизнь Эмилии Эрхарт Буква Oo [ou] оу под ударением
Буква Oo [ou] оу под ударением Практика speaking - говорения и listening - аудирования (умение слышать английскую речь)
Практика speaking - говорения и listening - аудирования (умение слышать английскую речь) Профессии. Образование названий профессий при помощи окончаний –er/ - or/ -ist
Профессии. Образование названий профессий при помощи окончаний –er/ - or/ -ist Poems Valentine ' s day
Poems Valentine ' s day English in Use 1. Form 9
English in Use 1. Form 9 Климат. Погода
Климат. Погода Team Leader YouLead’16
Team Leader YouLead’16 Презентация на тему Scotland the beautiful
Презентация на тему Scotland the beautiful  Present simple, present cont, past simple, future simple. Training
Present simple, present cont, past simple, future simple. Training Wild cats. Part 2
Wild cats. Part 2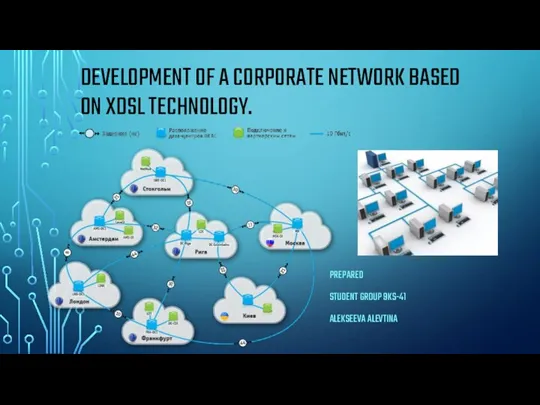 Development of a corporate network based on xDSL technology
Development of a corporate network based on xDSL technology My hometown
My hometown Horse race. Degrees of comparison
Horse race. Degrees of comparison Useful vocabulary
Useful vocabulary Презентация на тему Whether the weather
Презентация на тему Whether the weather  Презентация на тему Ball Of Flowers
Презентация на тему Ball Of Flowers  Sheet Concept Template
Sheet Concept Template Wild West. Past Simple. Vocabulary On America
Wild West. Past Simple. Vocabulary On America Exciting and interesting
Exciting and interesting