Содержание
- 2. Форма и размеры Земли
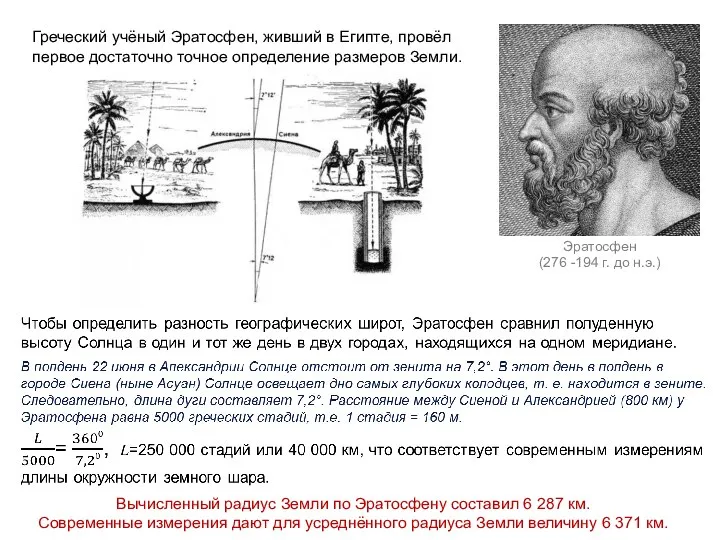
- 3. Греческий учёный Эратосфен, живший в Египте, провёл первое достаточно точное определение размеров Земли. Эратосфен (276 -194
- 4. Греческий учёный Эратосфен, живший в Египте, провёл первое достаточно точное определение размеров Земли. Эратосфен (276 -194
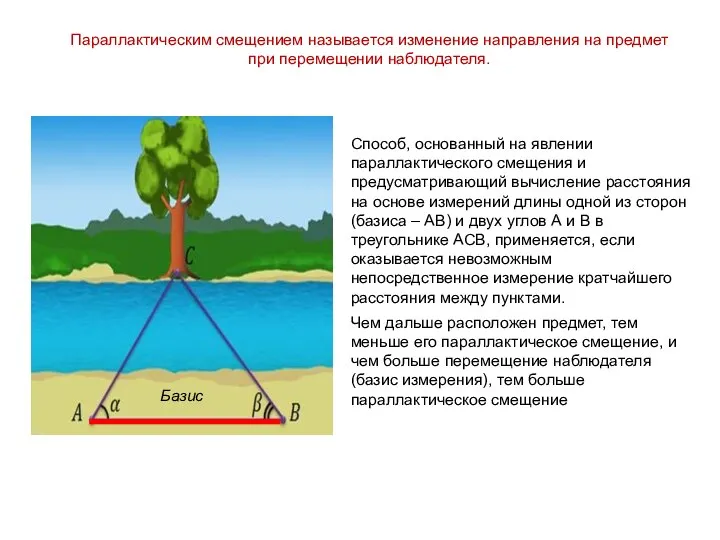
- 5. Способ, основанный на явлении параллактического смещения и предусматривающий вычисление расстояния на основе измерений длины одной из
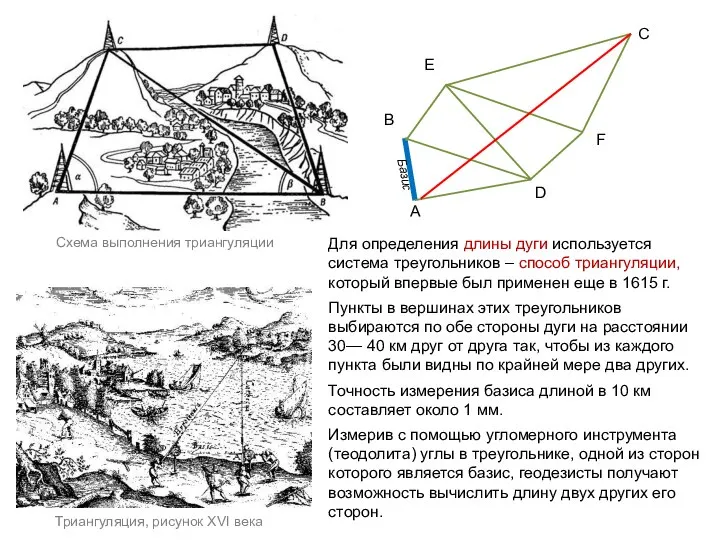
- 6. Для определения длины дуги используется система треугольников – способ триангуляции, который впервые был применен еще в
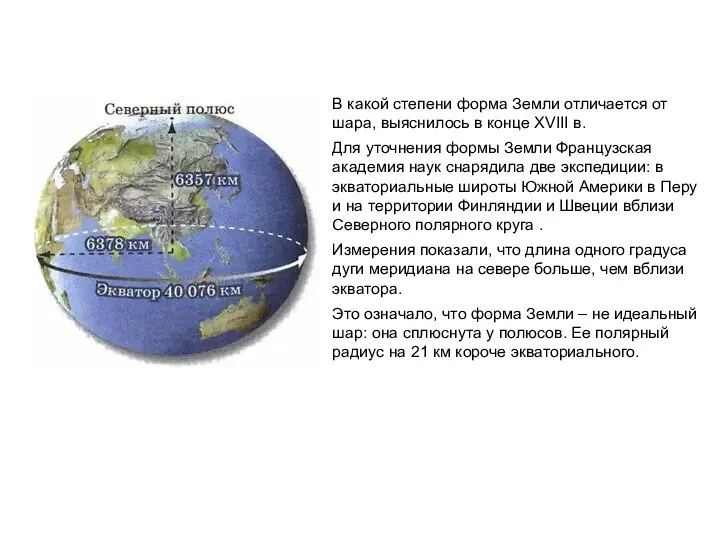
- 7. В какой степени форма Земли отличается от шара, выяснилось в конце XVIII в. Для уточнения формы
- 8. Для школьного глобуса масштаба 1: 50 000 000 отличие этих радиусов будет всего 0,4 мм, т.
- 9. В настоящее время форму Земли принято характеризовать следующими величинами: сжатие эллипсоида –1 : 298,25; средний радиус
- 10. Определение расстояний в Солнечной системе. Горизонтальный параллакс
- 11. Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда был впервые
- 12. Во второй половине XX в. развитие радиотехники позволило определять расстояния до тел Солнечной системы посредством радиолокации.
- 13. Определение размеров светил
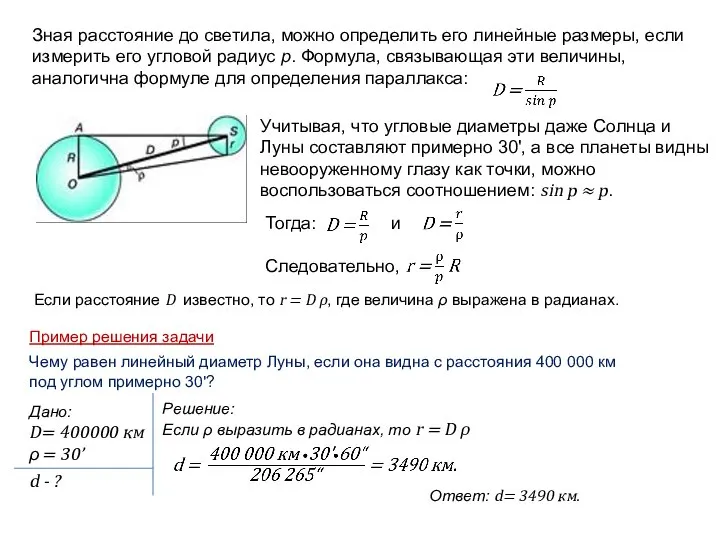
- 14. Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус р. Формула,
- 15. Вопросы 1. Какие измерения, выполненные на Земле, свидетельствуют о ее сжатии? 2. Меняется ли и по
- 17. Скачать презентацию









 Небесная сфера
Небесная сфера Плутон
Плутон Земля - одна из планет солнечной системы
Земля - одна из планет солнечной системы Сверхно́вые звёзды
Сверхно́вые звёзды История астрономии. Структура и масштабы Вселенной
История астрономии. Структура и масштабы Вселенной Эволюция звезд
Эволюция звезд Солнечная Система
Солнечная Система Лекция о космосе
Лекция о космосе Разработка алгоритма переориентации наноспутника формата CubeSat
Разработка алгоритма переориентации наноспутника формата CubeSat Космический мусор и его влияние на Землю
Космический мусор и его влияние на Землю Звезды и созвездия
Звезды и созвездия Презентация на тему Большое путешествие на луну
Презентация на тему Большое путешествие на луну  Шумеро-аккадская мифология с её планетой Нибиру
Шумеро-аккадская мифология с её планетой Нибиру Образование планетных систем. Солнечная система
Образование планетных систем. Солнечная система Выход в межзвёздное пространство
Выход в межзвёздное пространство Space technology
Space technology Пленеты солнечной системы: Сатурн
Пленеты солнечной системы: Сатурн Презентация на тему Метеориты (5 класс)
Презентация на тему Метеориты (5 класс)  Солнце, состав и внутреннее строение
Солнце, состав и внутреннее строение Астероиды с кометной активностью – новый тип объектов Солнечной системы
Астероиды с кометной активностью – новый тип объектов Солнечной системы Презентация на тему Мировая история освоения космоса
Презентация на тему Мировая история освоения космоса  Солнечное и Лунное затмения
Солнечное и Лунное затмения Планеты, которых нет
Планеты, которых нет ЕГЭ – 2018. Физика. Элементы астрофизики: Солнечная система, звезды, галактики
ЕГЭ – 2018. Физика. Элементы астрофизики: Солнечная система, звезды, галактики Галактики
Галактики Деймос. Естественный спутник Марса
Деймос. Естественный спутник Марса Мы во Вселенной. Земля - планета Солнечной системы
Мы во Вселенной. Земля - планета Солнечной системы SpaceX
SpaceX