Содержание
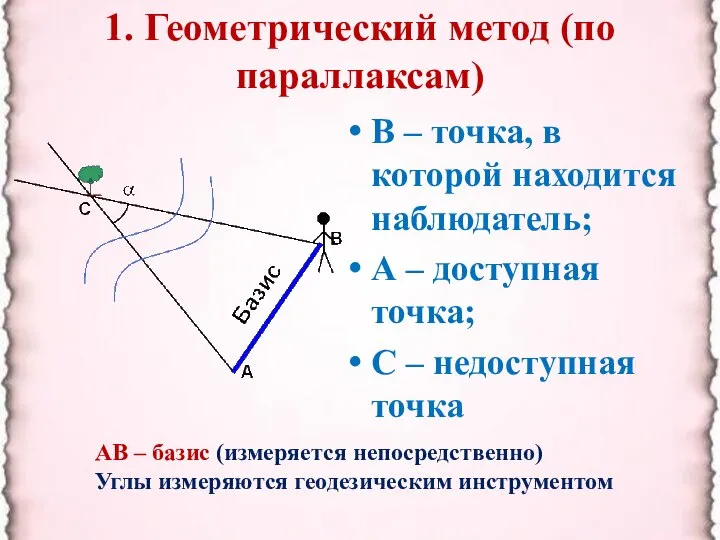
- 2. 1. Геометрический метод (по параллаксам) В – точка, в которой находится наблюдатель; А – доступная точка;
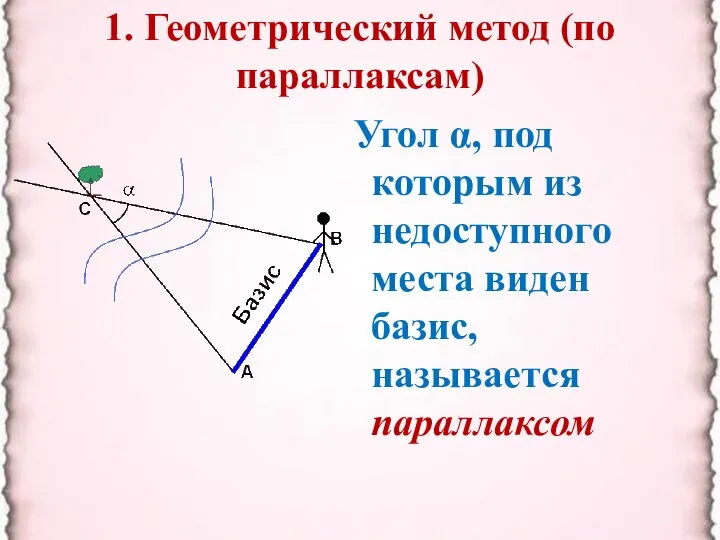
- 3. 1. Геометрический метод (по параллаксам) Угол α, под которым из недоступного места виден базис, называется параллаксом
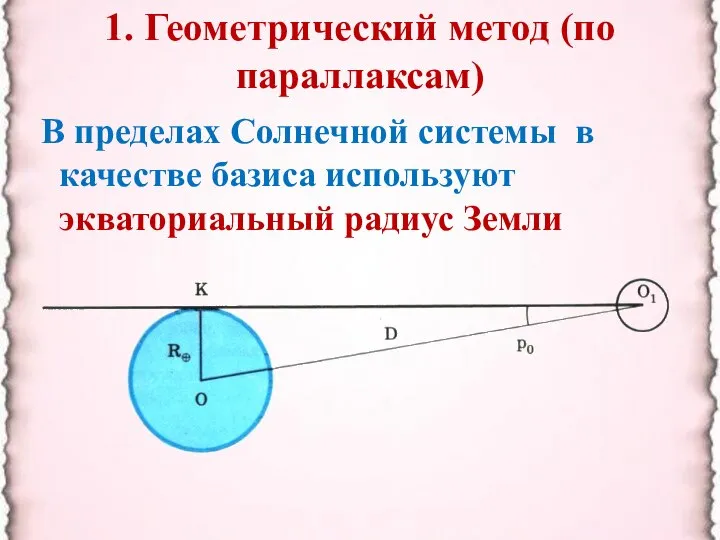
- 4. 1. Геометрический метод (по параллаксам) В пределах Солнечной системы в качестве базиса используют экваториальный радиус Земли
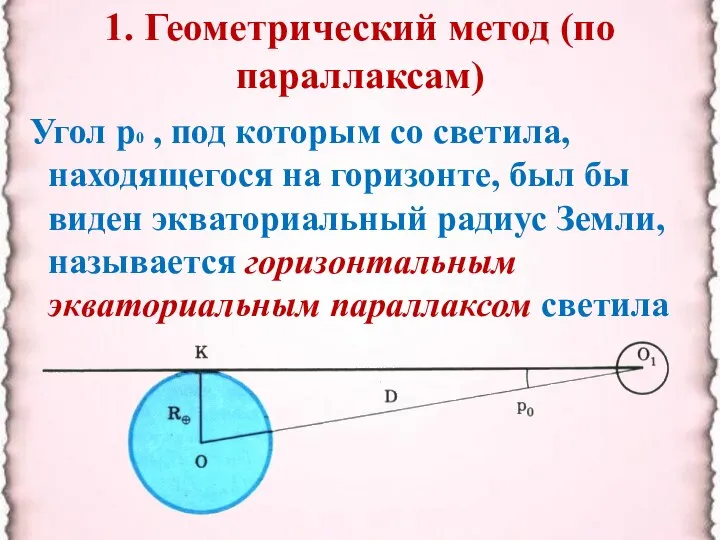
- 5. 1. Геометрический метод (по параллаксам) Угол р0 , под которым со светила, находящегося на горизонте, был
- 6. 1. Геометрический метод (по параллаксам) Если горизонтальный параллакс найден, то расстояние до светила вычисляется по формуле:
- 7. 1. Геометрический метод (по параллаксам) Поскольку углы р0 очень малы, то их синусы можно заменить самими
- 8. 1. Геометрический метод (по параллаксам) Тогда: Параллакс выражен в секундах дуги, а D – либо в
- 9. 2. Радиолокационный метод Радиолокация заключается в том, что на небесное тело посылают мощный кратковременный радиоимпульс, а
- 10. 2. Радиолокационный метод Зная скорость света в вакууме: с = 299 792 458 м/с и точно
- 11. 2. Радиолокационный метод Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы.
- 12. 3. Лазерная локация Метод аналогичен радиолокации, однако точность гораздо выше. Лазерная локация позволяет определять расстояния между
- 13. 4. Определение размеров тел Солнечной системы При наблюдениях небесных тел Солнечной системы можно измерить угол ρ,
- 14. 4. Определение размеров тел Солнечной системы Зная этот угловой радиус светила ρ и расстояние до светила
- 15. 4. Определение размеров тел Солнечной системы Учитывая ранее полученную формулу для D, получим:
- 16. 4. Определение размеров тел Солнечной системы А так как углы малы, то:
- 17. Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца 16´? Дано: Решение
- 19. Скачать презентацию












 Рождение, жизнь и смерть звёзд
Рождение, жизнь и смерть звёзд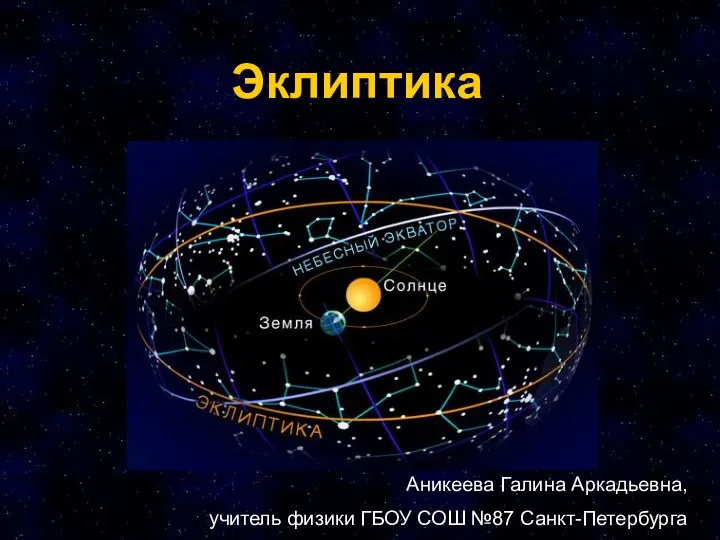 Эклиптика
Эклиптика День Космонавтики
День Космонавтики Законы движения планет Солнечной системы
Законы движения планет Солнечной системы Планеты Галактики
Планеты Галактики История появления названий небесных объектов
История появления названий небесных объектов 54-летию первого полета человека
54-летию первого полета человека Звездное небо. Созвездие Рыбы
Звездное небо. Созвездие Рыбы 12 апреля 2011 года – 50 лет первого полёта человека в космос – полёта Ю.А. Гагарина
12 апреля 2011 года – 50 лет первого полёта человека в космос – полёта Ю.А. Гагарина Направление подготовки Гидрометеорология
Направление подготовки Гидрометеорология Время первых. Покорители космоса
Время первых. Покорители космоса Млечный путь
Млечный путь Спутник Земли - Луна
Спутник Земли - Луна Космические советские плакаты
Космические советские плакаты Путешествие к планетам
Путешествие к планетам Созвездие Волк
Созвездие Волк Галактики
Галактики Луна важнее Солнца
Луна важнее Солнца Астрономія та визначення часу. Типи календарів
Астрономія та визначення часу. Типи календарів ПРЕЗЕНТАЦИЯ НА ТЕМУ
ПРЕЗЕНТАЦИЯ НА ТЕМУ Марс. Планета
Марс. Планета Подготовка космонавтов к полёту
Подготовка космонавтов к полёту Большой Новосибирский Планетарий
Большой Новосибирский Планетарий 2 апреля - День космонавтики. 4 класс
2 апреля - День космонавтики. 4 класс Меркурий
Меркурий Состав, строение и происхождение Солнечной системы
Состав, строение и происхождение Солнечной системы Земля в Солнечной системе
Земля в Солнечной системе Классификация галактик
Классификация галактик