Содержание
- 2. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Основные Элементы: Общая Теория Относительности (или альтернативная
- 3. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Существующие стандарты Общая Теория Относительности – резолюции
- 4. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Параметризованная теория систем отсчета: Ковариантна Калибровочно-инвариантна Оперирут
- 5. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Калибровочная свобода электродинамики Полевые переменные эл.-эм. поля
- 6. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Полевые переменные в гравитодинамике Метрический тензор Афинная
- 7. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Калибровочная инвариантность гравитодинамики
- 8. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Гармоническая калибровка и «остаточная» калибровочная свобода Гармонические
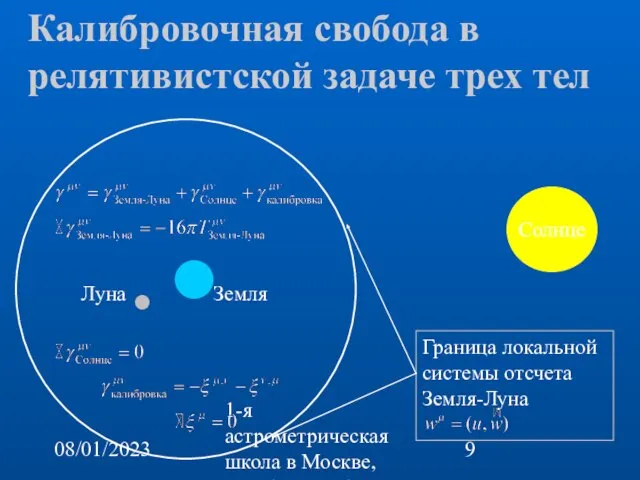
- 9. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Калибровочная свобода в релятивистской задаче трех тел
- 10. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Калибровочные степени свободы гравитационного поля в системе
- 11. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Примеры калибровочной свободы: TT-TCB преобразование времени Лоренцево
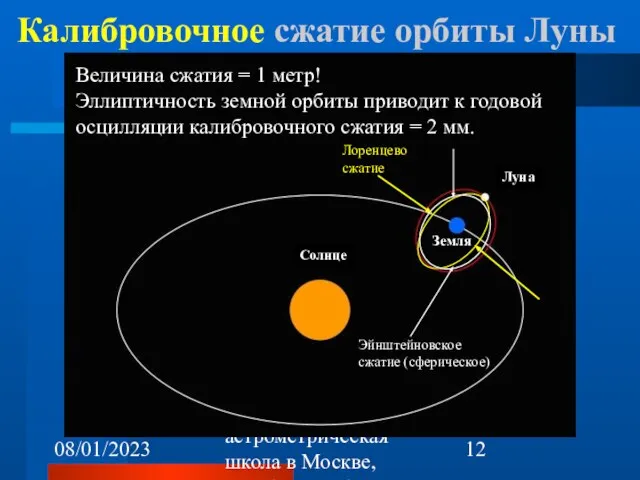
- 12. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Калибровочное сжатие орбиты Луны Величина сжатия =
- 13. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Являются ли калибровочные степени свободы наблюдаемыми? Эйнштейн:
- 14. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Аберрация и сокращение размеров движущихся тел В
- 15. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Калибровочные степени свободы в уравнениях Эйнштейна-Инфельда-Гоффмана для
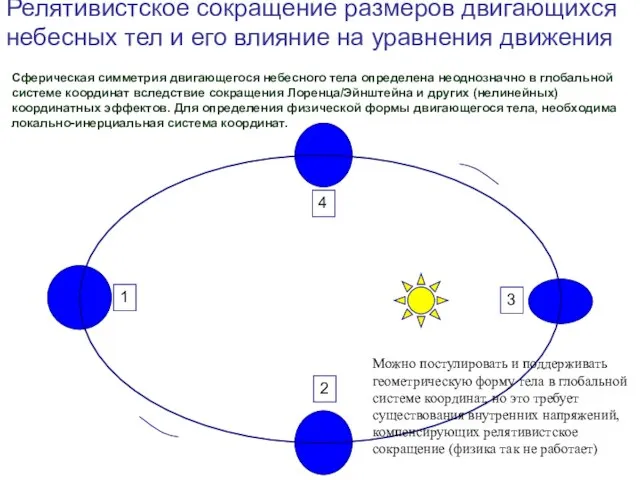
- 16. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Сферическая симметрия двигающегося небесного тела определена неоднозначно
- 17. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Пример: постулат сферической симметрии тел в глобальной
- 18. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Выводы: Калибровочная свобода в релятивистской гравитационной физике
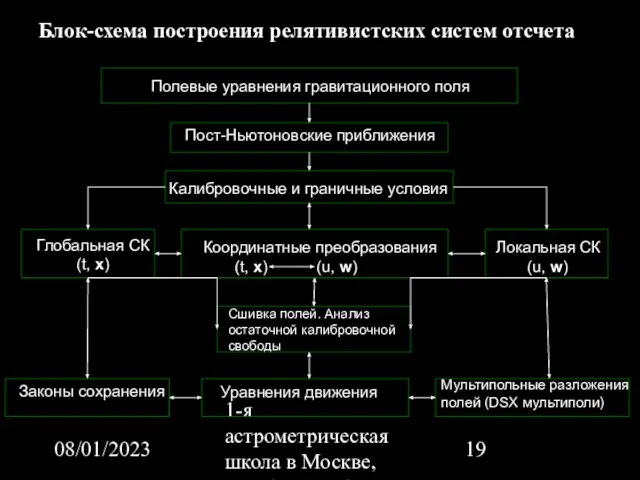
- 19. 08/01/2023 1-я астрометрическая школа в Москве, октябрь 22-26, 2007 Блок-схема построения релятивистских систем отсчета Полевые уравнения
- 21. Скачать презентацию














 Презентация на тему Вселенная
Презентация на тему Вселенная  Карликовые планеты
Карликовые планеты Жизнь и разум во Вселенной
Жизнь и разум во Вселенной Презентация на тему Квазары
Презентация на тему Квазары  Мир космоса. Виды летательных аппаратов
Мир космоса. Виды летательных аппаратов Иоганн Кеплер (1571-1630)
Иоганн Кеплер (1571-1630) Уран
Уран Теория большого взрыва
Теория большого взрыва Rabota_s_podvizhnoy_kartoy_zvezdnogo_neba
Rabota_s_podvizhnoy_kartoy_zvezdnogo_neba Венера. Анализ радарных карт Венеры
Венера. Анализ радарных карт Венеры Безбрежный космос
Безбрежный космос fizika
fizika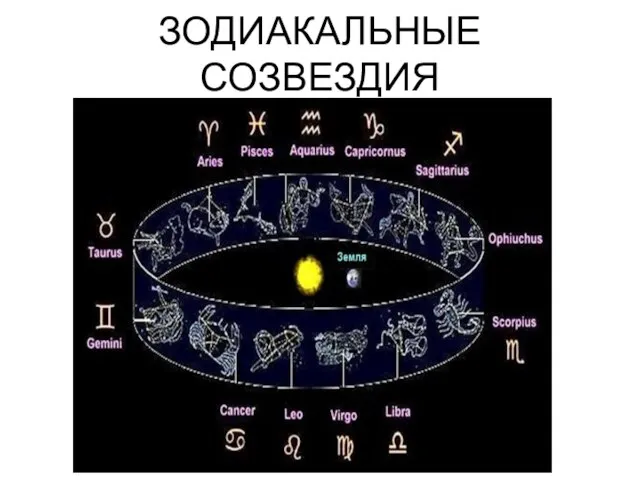 Зодиакальные созвездия
Зодиакальные созвездия Планеты Солнечной Системы
Планеты Солнечной Системы Астероиды и метеориты
Астероиды и метеориты Планеты Солнечной системыa
Планеты Солнечной системыa Межзвездные путешествия. Как, куда и зачем?
Межзвездные путешествия. Как, куда и зачем? БЦВМ КА
БЦВМ КА u1509281306
u1509281306 урок 1 предмет астрономии
урок 1 предмет астрономии Планета Меркурий
Планета Меркурий Космическая викторина
Космическая викторина Новый Марс. Каталог ресурсов
Новый Марс. Каталог ресурсов Движение планет и тригонометрия
Движение планет и тригонометрия Наша Галактика
Наша Галактика Происхождение Вселенной
Происхождение Вселенной Любительская астрономия
Любительская астрономия Астероиды солнечной системы
Астероиды солнечной системы