Тестирование релятивистских и космологических эффектов в Солнечной системе

Общая теория относительности
Изменение гравитационной постоянной G
Темная материя

DE ephemerides — Development Ephemeris,
Jet Propulsion Laboratory,
эфемериды DE, разработанные в
Лаборатории реактивного
движения,
(Пасадена, США)
EPM — Ephemerides of Planets and the Moon
(ИПА РАН, Россия)
INPOP ephemerides — Intégrateur Numérique Planétaire de l’Observatoire de Paris
(Париж, Франция)

Планетные эфемериды EPM2014
Численные эфемериды EPM2014 (Ephemerides of Planets and the Moon) были построены с использованием более 800 тысяч наблюдений (1913-2014 гг.) различных типов.
Уравнения движения тел брались в параметризованной постньютоновской метрике n-тел для Общей теории относительности в TDB шкале времени.
Интегрирование в барицентрической системе координат в шкале времени TDB на эпоху J2000.0 выполнялось методом Эверхарта на интервале 400 лет (1800-2200 гг.) лунно-планетным интегратором программного пакета ЭРА-7 (Krasinsky and Vasilyev, 1997).
Эфемериды EPM вместе с соответствующими разностями
TT–TDB, а также 7 дополнительными объектами: Ceres, Pallas, Vesta, Eris, Haumea, Makemake, Sedna доступны через FTP:
ftp://quasar.ipa.nw.ru/incoming/EPM/.

Динамическая модель EPM2014 учитывает
(помимо взаимных возмущений больших планет и Луны):
– возмущения от 301 наиболее массивных астероидов,
– возмущения от остальных малых планет главного пояса
астероидов, моделируемым притяжением двумерным
однородным кольцом,
– возмущение от 30 наибольших транснептуновых объектов.
– возмущения от остальных транснептуновых планет,
моделируемых однородным кольцом (на среднем
расстоянии 43 AE),
– релятивистские возмущения,
– возмущения от сжатия Солнца (2 ∙ 10-7 ),
– возмущения, вызываемые несферичностью фигур Земли и
Луны.

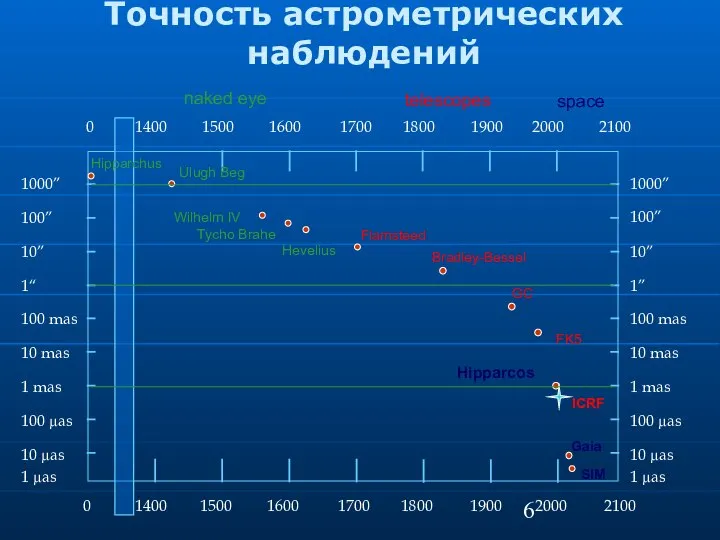
Точность астрометрических наблюдений

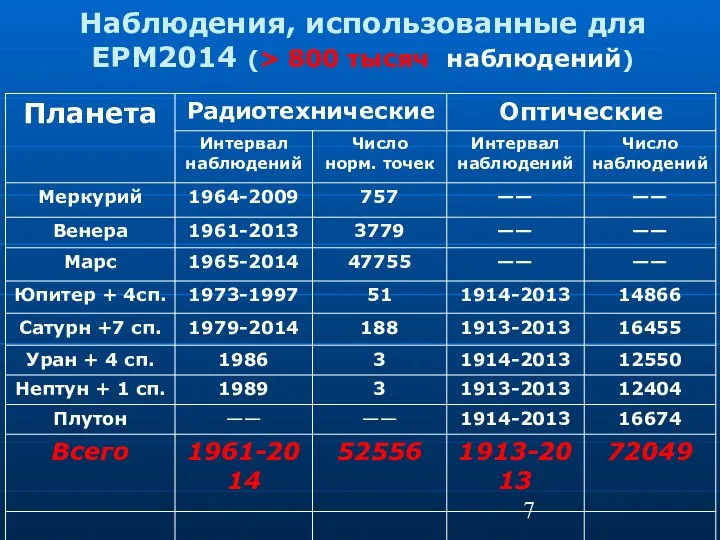
Наблюдения, использованные для EPM2014 (> 800 тысяч наблюдений)

Редукции радарных наблюдений
- релятивистские редукции ― запаздывание сигнала в гравитационных полях Солнца, Юпитера, Сатурна (эффект Шапиро) и редукция наблюдений от координатного времени эфемерид к собственному времени наблюдателя;
- запаздывание в тропосфере Земли;
- запаздывание в солнечной короне, параметры ее модели определяются из наблюдений для каждого соединения
( необходимы наблюдения на нескольких частотах !);
- поправки за топографию поверхностей планет (Меркурий, Венера, Марс).
Редукции оптических наблюдений
- опорные каталоги => FK4 => FK5 => ICRF;
- поправки за дополнительный эффект фазы (основные поправки за фазу внесены самими наблюдателями);
- релятивистские поправки за отклонение света.

В основном варианте улучшения планетной части EPM2014 эфемерид определялось около 270 параметров:
– элементы орбит планет и спутников внешних планет;
– величина астрономической единицы;
– углы ориентации эфемерид относительно ICRF;
– параметры вращения Марса и трех ПА на Марсе;
– массы около 30 астероидов, средние плотности
таксономических классов астероидов (C, S, M),
– масса главного астероидного пояса, масса кольца ТНО,
– отношение масс Земли и Луны;
– квадрупольный момент Солнца и параметры солнечной
короны для разных соединений планет с Солнцем;
– коэффициенты топографии Меркурия и поправки к
уровенным поверхностям Венеры и Марса;
– коэффициенты для дополнительного учета эффекта фазы
внешних планет.
– пост–модельные параметры (β, γ, движение π, ĠM◉/GM◉, Ġ/G, изменение ai).

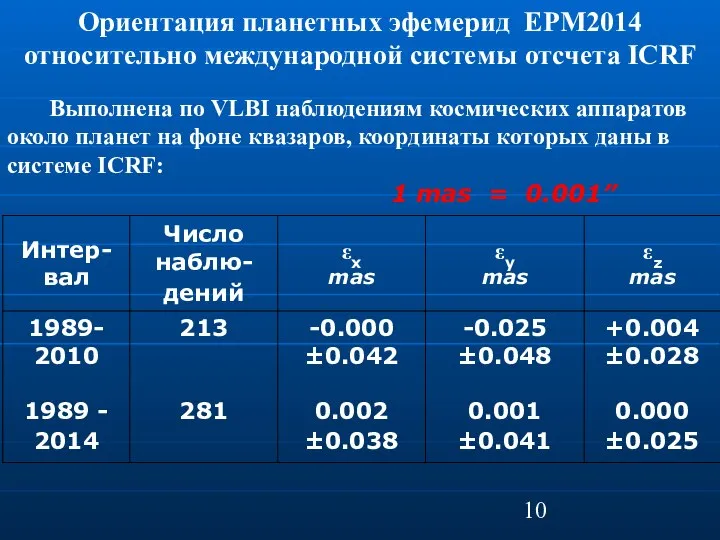
Ориентация планетных эфемерид EPM2014
относительно международной системы отсчета ICRF
Выполнена по VLBI наблюдениям космических аппаратов около планет на фоне квазаров, координаты которых даны в системе ICRF:
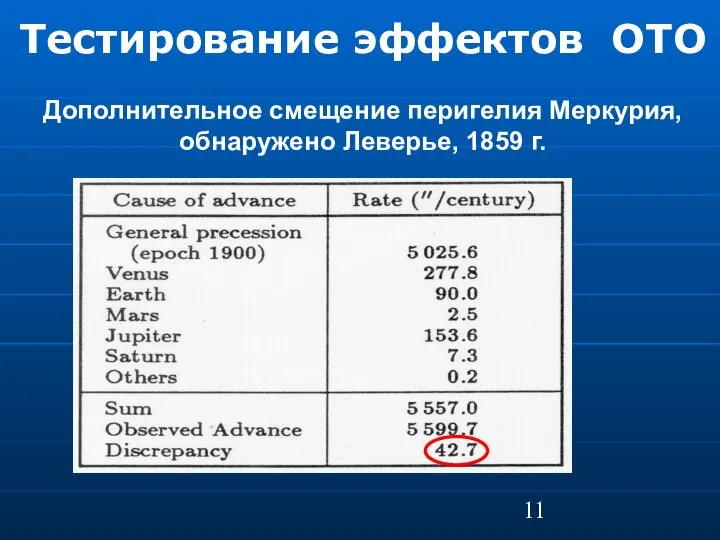
1 mas = 0.001”

Тестирование эффектов ОТО
Дополнительное смещение перигелия Меркурия, обнаружено Леверье, 1859 г.

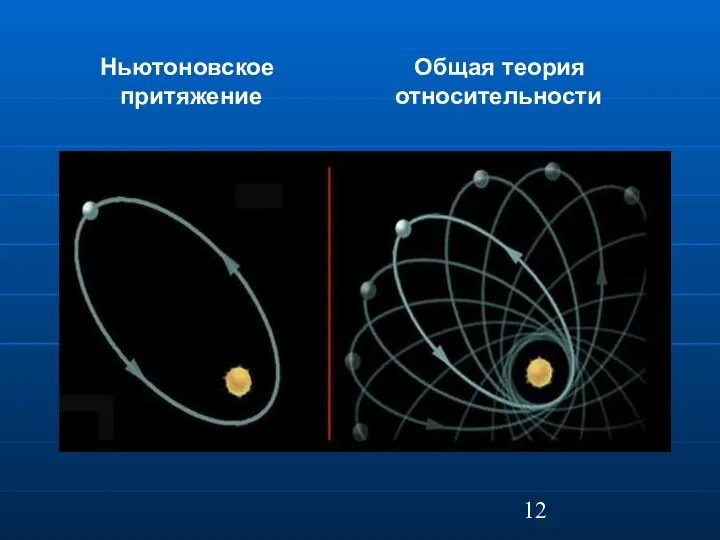
Ньютоновское Общая теория
притяжение относительности

Parametrized post-Newtonian (PPN) formalism
(Параметризованный пост-ньютоновский
PPN-формализм)
K. Nordtvedt, C. Will (1970-е)
Двумя самыми важными параметрами являются
γ и β ( γ =β =1 в ОТО )
Предсказания различных теорий гравитации могут быть выражены, используя эти параметры

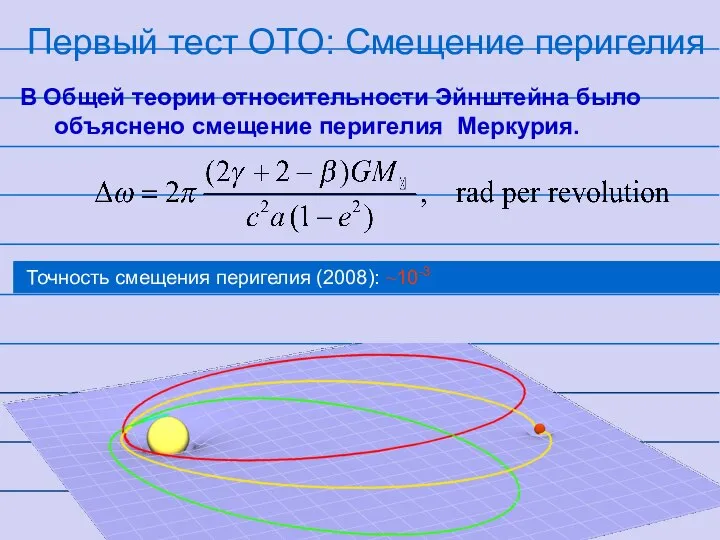
Первый тест ОТО: Смещение перигелия
В Общей теории относительности Эйнштейна было объяснено смещение перигелия Меркурия.
Точность смещения перигелия (2008): ~10-3

Второй тест Общей теории относительности: отклонение света
Возможные результаты:
- Нет отклонения = 0
- Ньютон = 0.87″
- Эйнштейн = 1.75″
Прав оказался Эйнштейн

Третий тест ОТО: эффект Шапиро
Свету требуется больше времени, чтобы пройти расстояние от излучателя до приемника, чем просто расстояние между ними, деленное на скорость света
Открыт Ирвином Шапиро в 1964 году как теоретическое предсказание Общей теории относительности, первые измерения, сделанные в конце 1960-х годов подтвердили
значение Шапиро с точностью 10%.

PPN параметры β и γ
(General Relativity: β = γ = 1)
Полученные нами результаты:
β - 1 = −0.00002 ± 0.00003, γ - 1 = +0.00004 ± 0.00006
=> соответствие планетных движений и распространения света ОТО
Французские коллеги (Fienga et al., 2015) получили аналогичные результаты на основе своих численных эфемерид INPOP13:
(готовится статья в Celestial Mechanics Dyn. Astr., 2015)
β - 1 = 0.00000 ± 0.00007, γ - 1 = - 0.00002 ± 0.00005,

Изменение G во времени
Если G зависит от времени, то движение планет будет происходить с изменениями полуосей и появится дрейф периодов орбитального движения планет

Из наблюдений движения планет можно
получить, как меняется гелиоцентрическая гравитационная постоянная Солнца GMΘ

Гелиоцентрическая гравитационная постоянная
=(132712440041±10) км3сек-2 (МАС, 2009)
Средняя полная светимость Солнца L◉ = 3.846 • 1033 эрг/с ,
(Willson R. C., et al., 1986, Science, 234, 1114 )
Масса Солнца M = 1.9891 • 1033 г
(Brun A.S., et al., 1998 Astrophys. J., 506, 913-925),
Гравитационная постоянная
G=(6.67428 ±0.00067) • 10-11 м3/кг сек2 (CODATA 2006)
Астрономическая единица АЕ=(149597870700 м (МАС, 2012)
Некоторые параметры

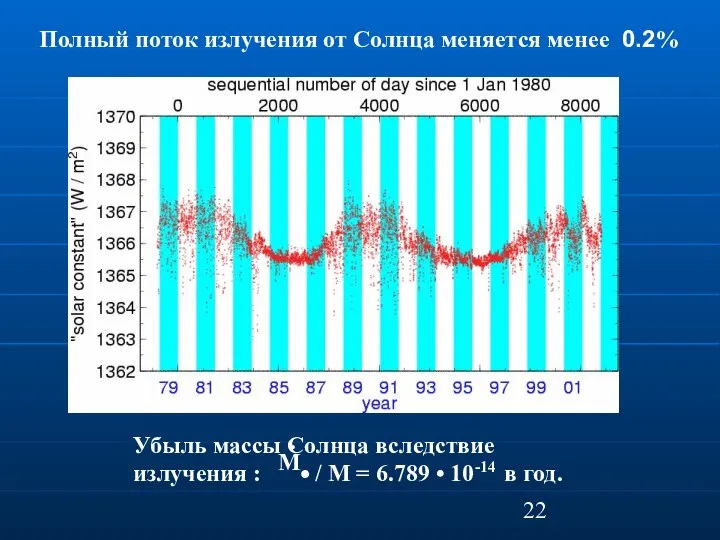
Убыль массы Солнца вследствие излучения:
= - 6.789 • 10-14 в год.
Убыль массы Солнца вследствие солнечного ветра:
= - 2 • 10-14 в год.
(Hundhausen, 1997; Meyer-Vernet N., 2007)
Также указывают для солнечного ветра
= - (2-3) • 10-14 в год.
(Carroll, Ostlie, 1996; Livingston, 2000)
Совместный эффект уменьшения за счет излучения и солнечного ветра:
Уменьшение массы Солнца

Полный поток излучения от Солнца меняется менее 0.2%
Убыль массы Солнца вследствие излучения : / M = 6.789 • 10-14 в год.
.
M◉

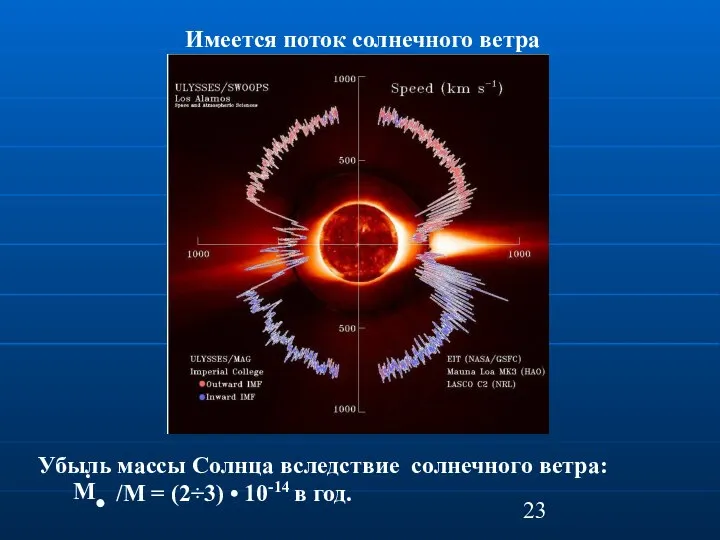
Имеется поток солнечного ветра
Убыль массы Солнца вследствие солнечного ветра:
/M = (2÷3) • 10-14 в год.
.
M◉

Возрастание массы Солнца
Существует обратный процесс – увеличение массы Солнца:
– за счет падения метеорного и астероидного вещества на Солнце;
– за счет вещества, приходящего из дальних областей Солнечной системы, главным образом, в форме комет (из занептуновых областей - пояс Койпера, облако Оорта).
В большое число комет из семейства Крейтца регистрируется в непосредственной близости от Солнца (sungrazing comet) с помощью коронографа LASCO, установленного на солнечной космической обсерватории SOHO (http://lasco-www.nrl.navy.mil/) + обсерватория SDO (NASA).

В среднем, орбитальные обсерватории SOHO и SDO фиксируют изображения комет Крейтца один раз в три дня
Kamikaze Comet С/2011 N3
(в ночь с 5 на 6 июля, 2011)

Good-bye, Kamikaze Comet (October 3, 2011)

Comet ISON
(C/2012 S1)
Discovery date:
21 September 2012
Eccentricity 0.9999947
1.0002
Last perihelion
28 November 2013

Падение вещества на Солнце
Падение пыли: < < (10-16 ÷ 10-17) в год
Общая масса астероидов главного пояса, представленная суммой масс 301 крупнейших астероидов и астероидного кольца:
Mbelt = (12.3 ±1.1 ) • (≈ 3 массы Цереры).
(Pitjeva, Pitjev 2013)
Падение астероидов: < (10-16 ÷ 10-17) в год
Для оценки сверху падающей массы с кометами можно воспользоваться статистикой комет SOHO и принять, что все они имеют крупные ядра и сгорают в короне или падают на Солнце. Тогда получим завышенную оценку сверху

Общий интервал для изменения
Для получения нижней границы возьмем максимальную оценку убыли за счет солнечного ветра и одновременно положим полное отсутствие падения вещества на Солнце.
Для верхней границы используем максимальную оценку падающего материала на Солнце и положим нулевую убыль массы с солнечным ветром.
Тогда получим

Влияние на орбитальные элементы планет
Задача двух тел с переменной массой имеет давнюю историю: Гюльден (1884), Мещерский (1893), Стремгрен (1903), Пламмер (1906) и др.
Рассматривается вариант изотропного изменения массы центрального тела без появления реактивных сил.
Сходная задача возникает при рассмотрении возможного изменения гравитационной постоянной в рамках гипотезы Дирака (1938).
Если обозначить μ(t)=G(M+m), то векторное уравнение относительного движения запишется
Поскольку поле остается центральным, сохраняется векторный интеграл площадей

Учитывая монотонность и малость , можно показать (Jeans, 1924), что выполняется инвариант
μ(t)·a(t) = const, где a – полуось орбиты.
Отсюда = - .
Из интеграла площадей получается соотношение
μ(t)·a(t) ·(1-e2) = c2, c=|c|,
откуда следует, что при рассматриваемых условиях эксцентриситет оскулирующей орбиты сохраняется
e = const (Jeans, 1925).
При принятых условиях малости и монотонности изменения μ(t) аргумент перицентра не имеет векового тренда (Kevorkian, Cole, 1996) .

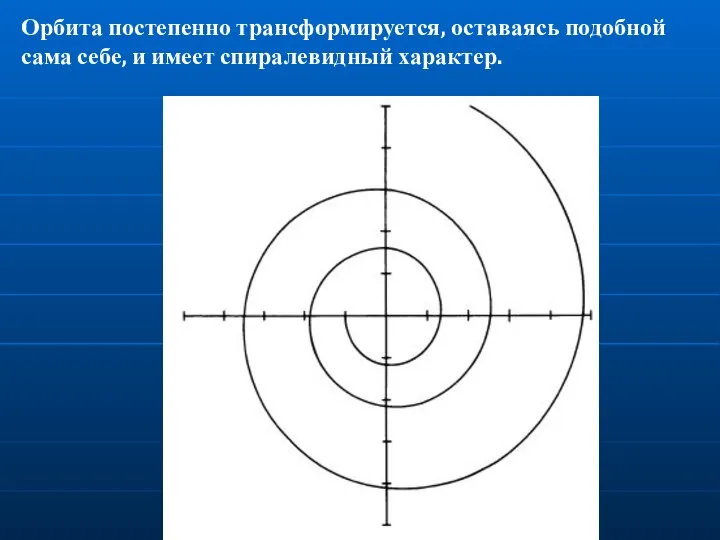
Орбита постепенно трансформируется, оставаясь подобной сама себе, и имеет спиралевидный характер.

Полученные значения изменения
(MNRAS, 2013)
Наиболее достоверно определяется изменение гелио-
центрической гравитационной постоянной (точность растет пропорционально квадрату интервала времени наблюдений) :
= (-6.3 ± 4.2)•10-14 в год (2σ)
Одновременно были найдены вековые изменения больших полуосей планет. Положительные значения для планет с высокоточными наблюдениями подтверждают уменьшение – для полуосей Меркурия, Венеры, Земли, Марса, Юпитера и Сатурна.
Для полуосей Урана и Нептуна получились отрицательные значения, для Плутона – положительное, но эти результаты недостоверны из-за недостаточной точности наблюдательных данных для этих планет.

Из полученного результата для можно получить оценку для , используя соотношение
Можно записать, что с вероятностью 95 % (2σ)
Отсюда, используя найденные ограничения для
,
находим, что с вероятностью 95 % значение находится в интервале
Оценка , полученная по данным лазерной локации Луны (Turyshev & Williams, 2007), дает следующие пределы для изменения G:
= (6±7)·10-13 в год.

Найденное изменение , вероятно, отражает изменение именно , а не G
Это значение попадает в интервал ограничений для
и, по всей видимости, отражает баланс между теряемой массой через излучение и солнечный ветер и падающим материалом, содержащимся в кометах и падающих каменистых обломках и астероидах.
Французские коллеги получили (Fienga, et al., 2015) следующие оценки:
Статья вышла в Celestial Mechanics Dyn. Astr., 2015.
= (- 4.3 ± 5.0) •10-14 год-1 , (2σ)
= ( 4.9 ± 10.5) •10-14 год-1 (2σ)

Темная материя
в Солнечной системе
В современной космологии
слово Dark стало использоваться часто :
Dark Energy – темная энергия
Dark Matter – темная материя
Dark Forces – темные силы
Dark Dynamics – темная динамика
Dark Cosmology – темная космология
Dark Age – темная эпоха
Dark Worlds – темные миры
Dark radiation – темное излучение
Dark sector – темная часть Вселенной

Организованы
Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen
Journal "Physics of the Dark Universe"
International Workshop on the Dark Side of the Universe
и т.д.

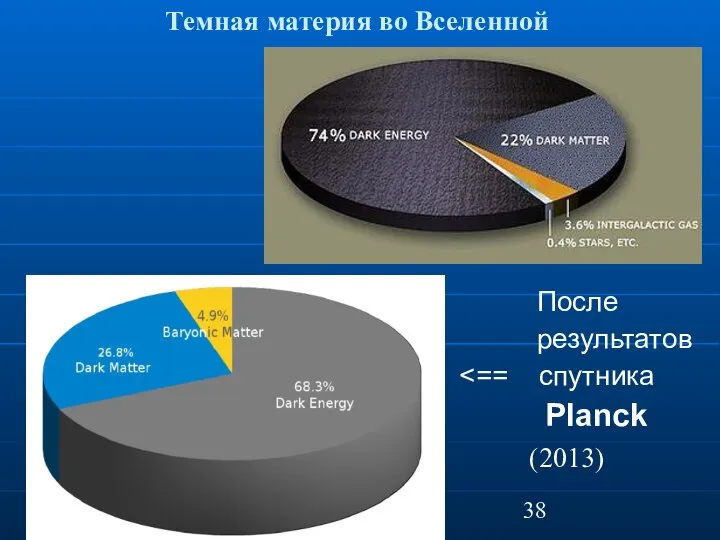
Темная материя во Вселенной
После
результатов
<== спутника
Planck
(2013)

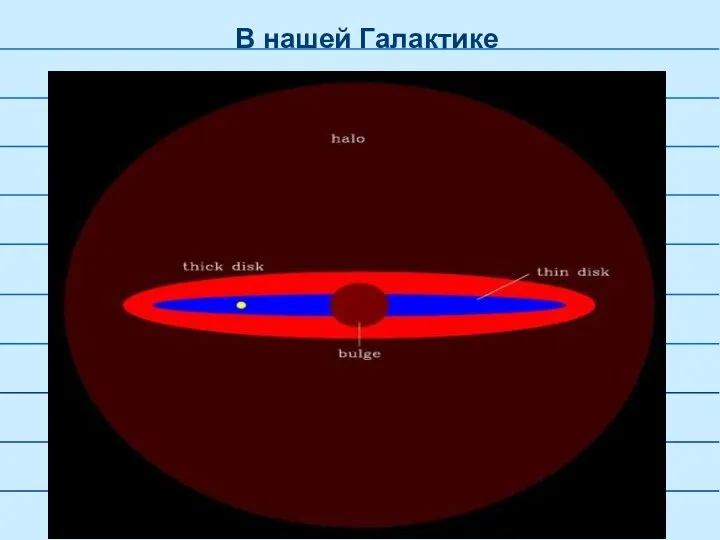
В нашей Галактике

Для поиска и исследования частиц темного вещества (WIMPs) или следов его возможного взаимодействия построены специальные экспериментальные установки (CRESST, CoGeNT, DAMA, XENON100, PAMELA, FERMI, HESS, CDMS, ANTARES, WMAP, SPT и др.), и строятся новые.
Плотность темной материи в гало нашей Галактики оценивается на уровне
ρdm ≈ 5 •10 -25 г/см3
XENON100 - в итальянской подземной лаборатории Гран-Сассо
LUX - новый ксеноновый детектор (2013), смонтирован в тоннелях старой золотоносной шахты, Сэнфордская подземная лаборатория (США) .

Дополнительная центральная масса
Есть дополнительное ускорение от распределенной материи:
(d2r/dt2)dm = - GM(r)dm /r2 , (1)
где M(r)dm – масса распределенной материи, заключенной в сфере радиуса r вокруг Солнца.
При однородной плотности ρ распределенной гравитирующей среды, заполняющей солнечную систему, дополнительное ускорение будет пропорционально r:
(d2r/dt2)dm = - kr . (2)

Дополнительное смещение перигелия
Если для единичной массы через E, J обозначить значения интегралов энергии и площадей, через U(r) – сферически симметричный потенциал, то уравнение движения по радиусу r запишется
dr/dt = { 2[E+U(r)] - (J/r)2 }1/2 , (3)
Уравнение движения по азимутальной координате θ
dθ/dr = J/r2 /{ 2[E+U(r)] - (J/r)2 }1/2 . (4)

Наличие некоторой дополнительной распределенной материи приводит к более короткому радиальному периоду и к отрицательному дрейфу перицентра и апоцентра (в противоположную движению планеты сторону):
Δθ0 = -4π2ρdm /MSun • a3(1-e2)1/2 (5)
где Δθ0 - смещение перигелия за одно полное радиальное колебание.

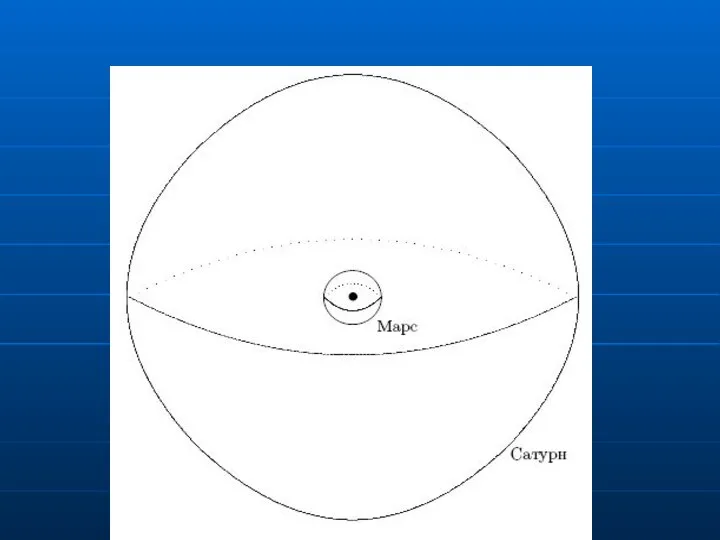
Прецессия орбиты

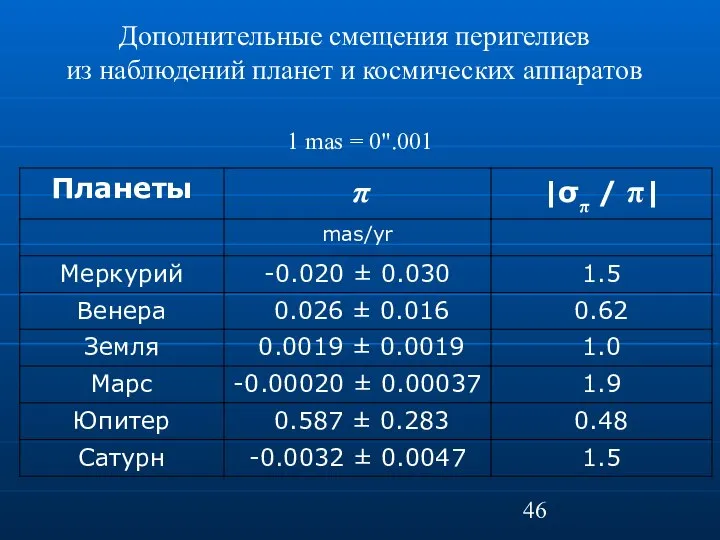
Дополнительные смещения перигелиев
из наблюдений планет и космических аппаратов
1 mas = 0".001

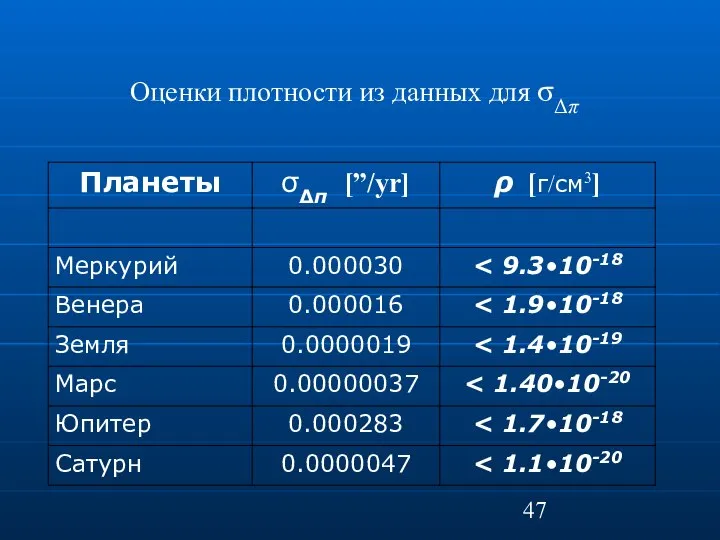
Оценки плотности из данных для σΔπ

Оценки при однородном распределении плотности
Если исходить из предположения об однородном распределении ρdm в Солнечной системе, то из данных для Сатурна получается наиболее сильная ограничивающая оценка
ρdm < 1.1•10-20 г/см3.
Тогда внутри сферического объема с размерами орбиты Сатурна масса
Mdm < 7.1•10-11 MSun .
Эта величина меньше погрешности определения полной массы главного астероидного пояса.

В качестве модели распределения с концентрацией к центру
взято следующее выражение для плотности:
ρdm = ρ0 • e-cr , (6)
где параметр ρ0 – центральная плотность, c – коэффициент экспоненциального падения плотности к периферии.
Гравитационный потенциал, создаваемый сферически распределенной материей с плотностью (6), будет
U(r) = 4πG ρ0 /r •[2- e-cr (cr+2)]/c3 (7)
Параметры распределения (6) могут быть оценены по полученным результатам.
Масса внутри сферы радиуса r для распределения (6) равна
Mdm = 4π ρ0 [2/c3 – e-cr (r2/c + 2r/c2 + 2/c3)] (8)
Оценки при экспоненциальном распределении плотности

Оценка массы темной материи до орбиты Сатурна найдена
из оценивания масс на двух интервалах: от Сатурна до Марса и
от Марса до Солнца. Для этого были использованы наиболее
надежные данные в табл. для Сатурна (ρdm < 1.1•10-20 г/см3), Марса (ρdm < 1.4•10-20 г/см3) и Земли (ρdm < 1.4•10-19 г/см3).
Между Марсом и Сатурном по данным для Марса и Сатурна получился очень пологий ход плотности с
ρ0 = 1.47•10-20 г/см3 и c =0.0299 ае-1 .
На интервале Марс – Солнце полученный ход плотности по данным для Земли и Марса дает крутой подъем к Солнцу с параметрами
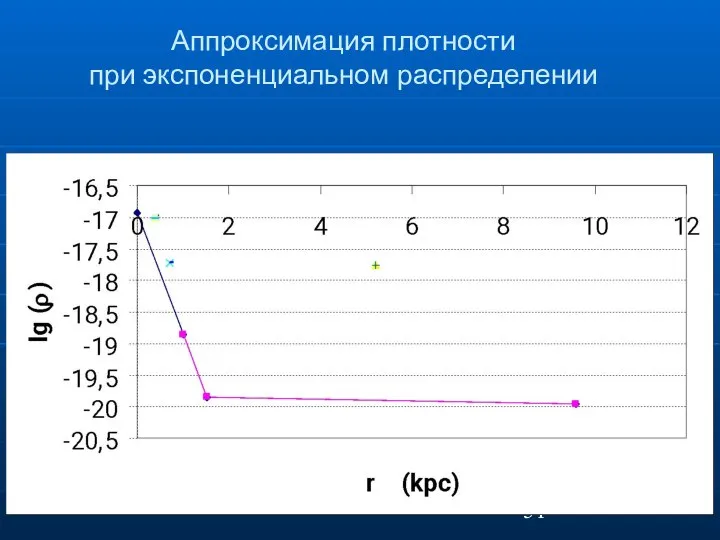
ρ0 = 1.17•10-17 г/см3 и c =4.42 ае-1 .

Аппроксимация плотности
при экспоненциальном распределении

Масса в объеме между орбитами Марса и Сатурна
Mdm < 7.33•10-11 MSun.
Масса (14) между Солнцем и орбитой Марса оказалась
Mdm < 0.55•10-11 MSun .
Включая оба интервала, верхняя граница для общей массы
темной материи до орбиты Сатурна с учетом ее возможной концентрации к центру получилась
Mdm < 7.88•10-11 MSun ,
то есть тоже порядка погрешности определения полной массы астероидного пояса ± 1.13•10-10 MSun (3σ)

Результаты для темной материи
Уровень распределенной плотности темной материи
ρdm , если она имеется, очень мал и существенно ниже
современной погрешности определения таких параметров.
Найдено, что на расстоянии орбиты Сатурна плотность
должна быть ниже, чем
ρdm < 1.1•10-20 г/см3 ,
а масса темной материи в сфере внутри орбиты Сатурна
даже с учетом ее возможной концентрации к центру
должна быть меньше чем
Mdm < 7.9•10-11 MSun .
2013, Astronomy Letters, vol. 39, p. 141-149;
2013, MNRAS 432, 3431–3437
.