Содержание
- 2. 1. КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ Картографической проекцией называется математически определенный способ отображения поверхности земного эллипсоида на плоскости
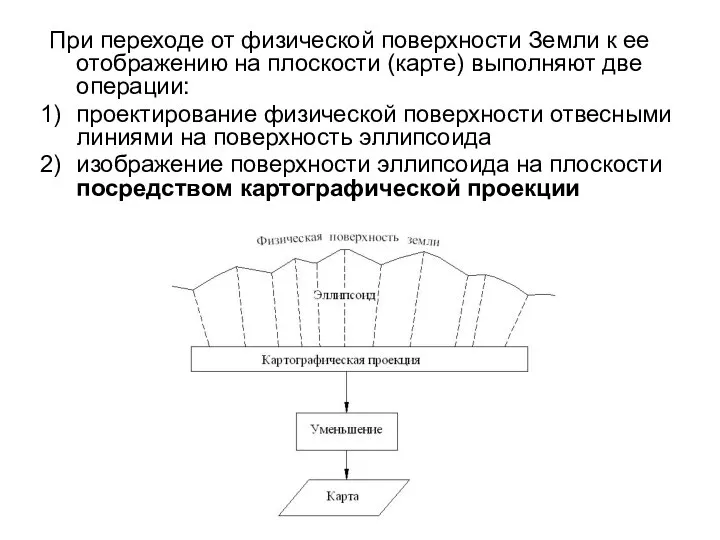
- 3. При переходе от физической поверхности Земли к ее отображению на плоскости (карте) выполняют две операции: проектирование
- 4. Наличие искажений в картографических проекциях, применяемых для географических карт, неизбежно, так как земная поверхность, имеющая форму
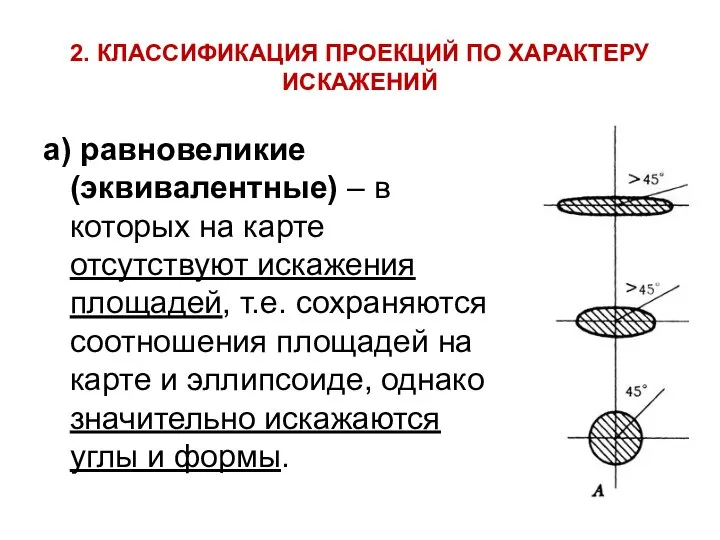
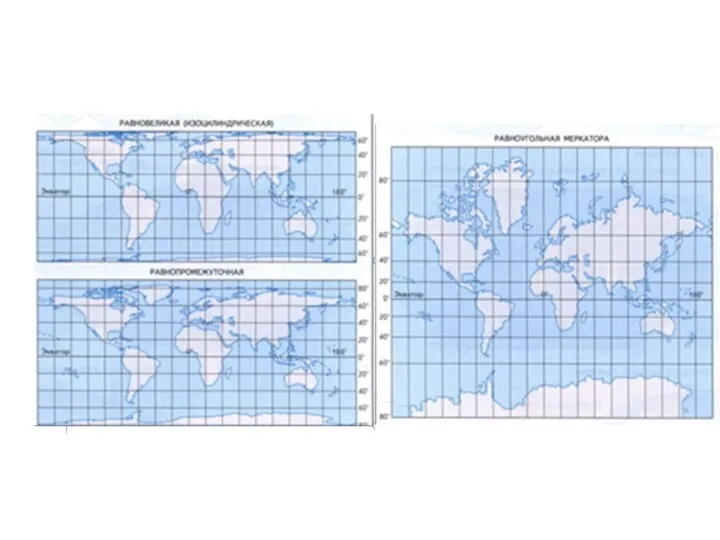
- 5. 2. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ХАРАКТЕРУ ИСКАЖЕНИЙ а) равновеликие (эквивалентные) – в которых на карте отсутствуют искажения
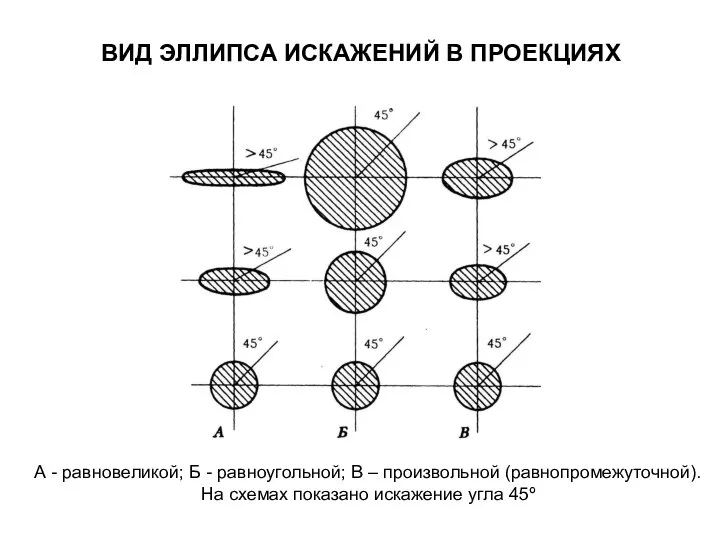
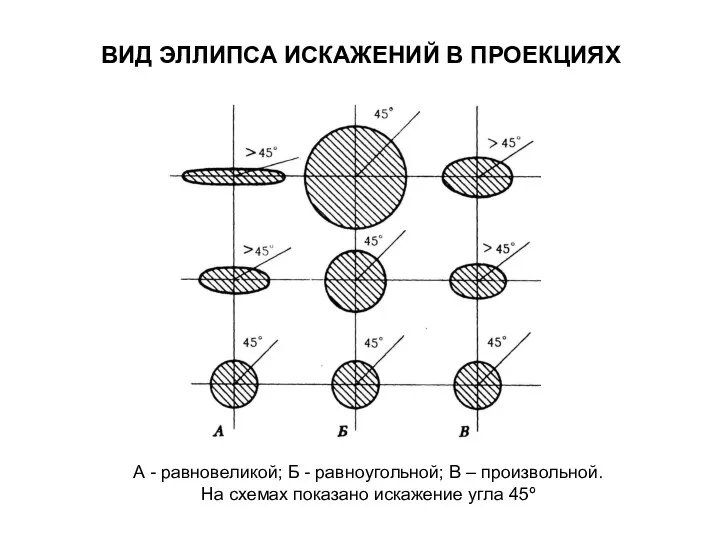
- 8. ВИД ЭЛЛИПСА ИСКАЖЕНИЙ В ПРОЕКЦИЯХ А - равновеликой; Б - равноугольной; В – произвольной (равнопромежуточной). На
- 9. Искажения в равновеликой циллиндрической проекции В равновеликих проекциях окружность, взятая на поверхности эллипсоида сохраняет свою площадь,
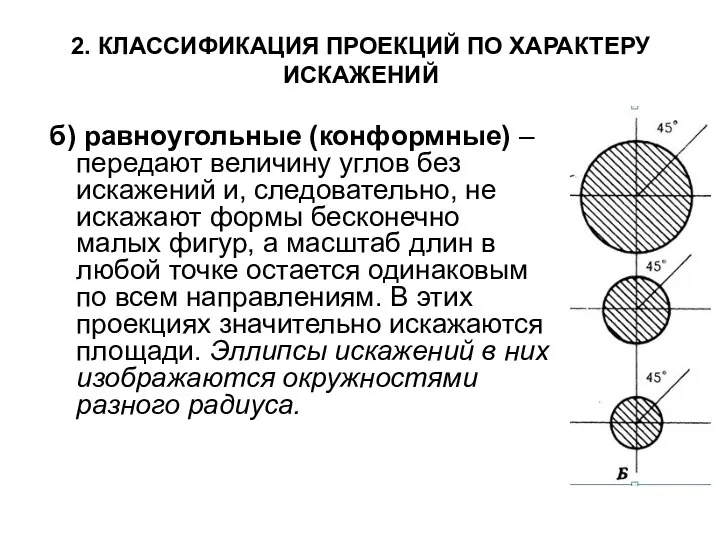
- 12. 2. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ХАРАКТЕРУ ИСКАЖЕНИЙ б) равноугольные (конформные) – передают величину углов без искажений и,
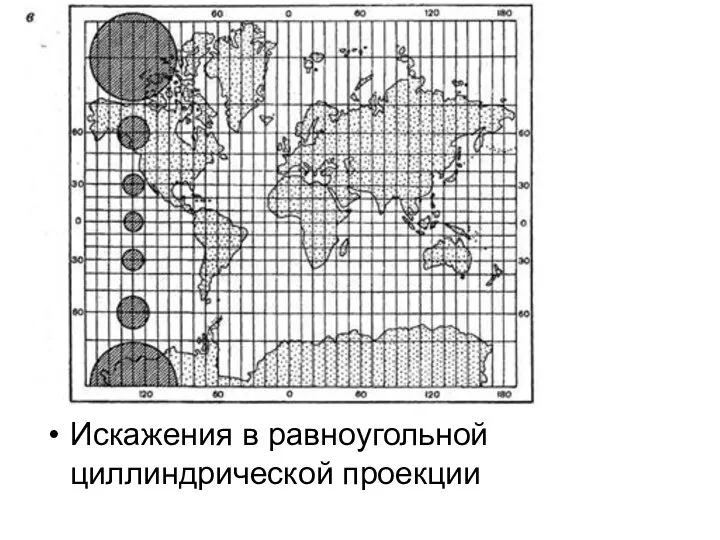
- 13. Искажения в равноугольной циллиндрической проекции
- 14. Равноугольные проекции широко используются на навигационных картах, так как они удобны для определения направлений и прокладки
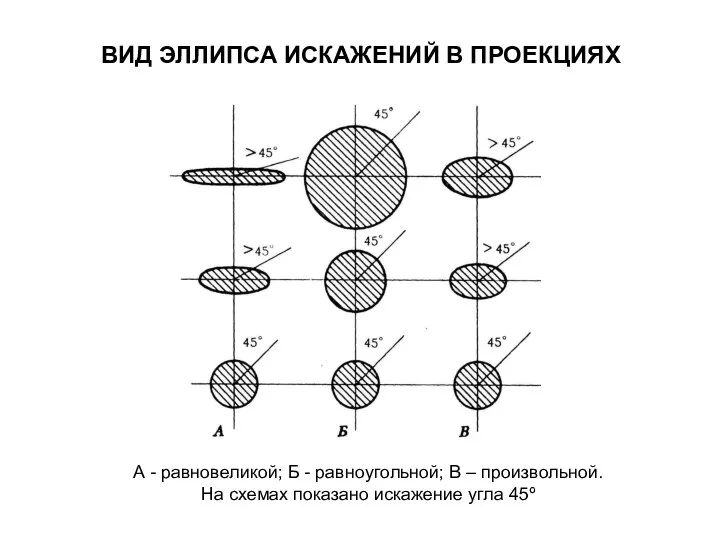
- 15. ВИД ЭЛЛИПСА ИСКАЖЕНИЙ В ПРОЕКЦИЯХ А - равновеликой; Б - равноугольной; В – произвольной. На схемах
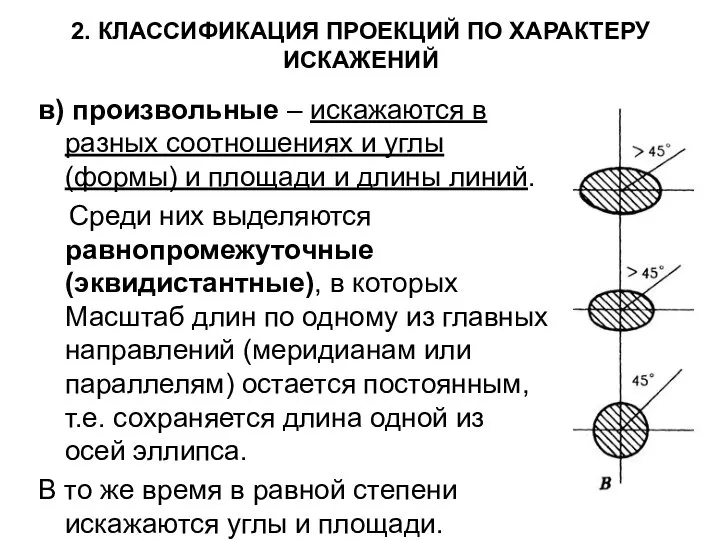
- 16. 2. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ХАРАКТЕРУ ИСКАЖЕНИЙ в) произвольные – искажаются в разных соотношениях и углы (формы)
- 17. Искажения в равнопромежуточной циллиндрической проекции
- 19. ВИД ЭЛЛИПСА ИСКАЖЕНИЙ В ПРОЕКЦИЯХ А - равновеликой; Б - равноугольной; В – произвольной. На схемах
- 20. 3. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ СЕТКИ ПАРАЛЛЕЛЕЙ И МЕРИДИАНОВ В зависимости от вида геометрической поверхности,
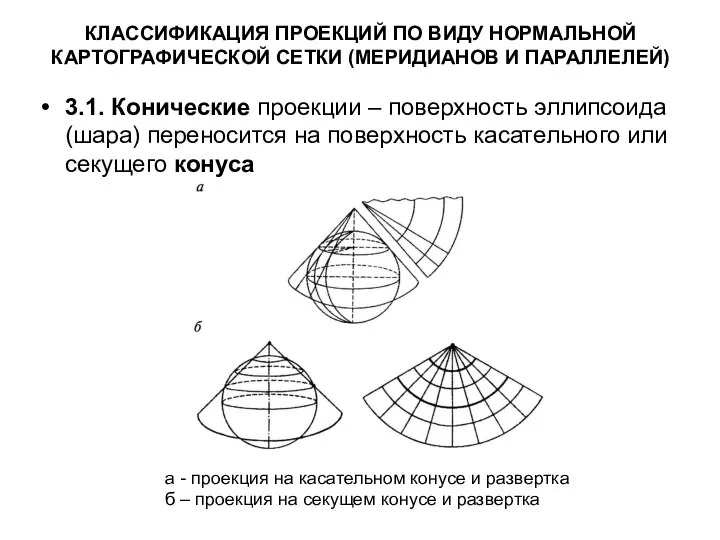
- 21. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) 3.1. Конические проекции – поверхность эллипсоида
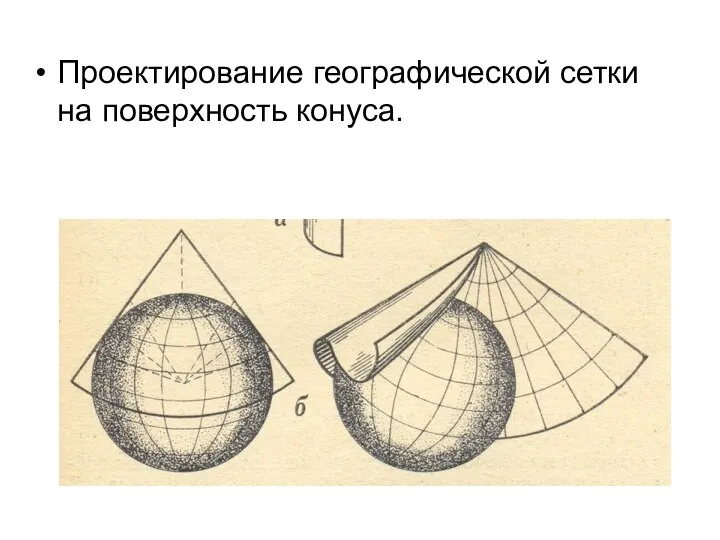
- 22. Проектирование географической сетки на поверхность конуса.
- 23. ВИДЫ ПРОЕКЦИЙ ПО ОРИЕНТИРОВКЕ ВСПОМОГАТЕЛЬНОЙ ПОВЕРХНОСТИ на примере конических проекций
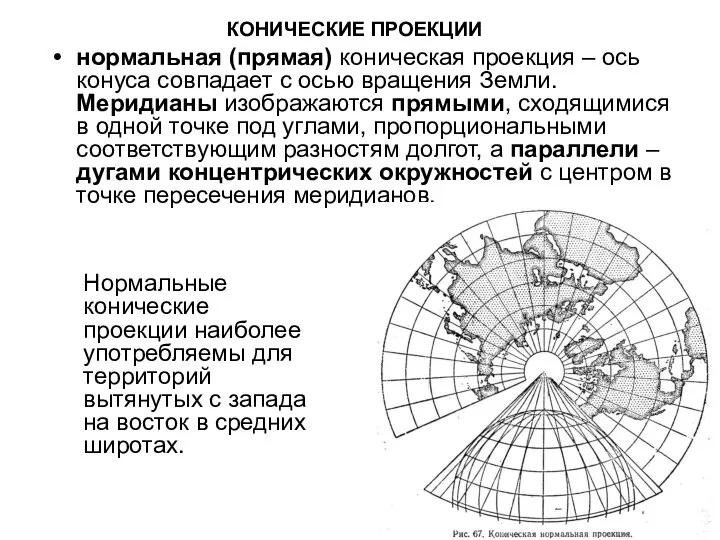
- 24. КОНИЧЕСКИЕ ПРОЕКЦИИ нормальная (прямая) коническая проекция – ось конуса совпадает с осью вращения Земли. Меридианы изображаются
- 26. КОНИЧЕСКИЕ ПРОЕКЦИИ поперечная коническая проекция – ось конуса лежит в плоскости экватора В поперечных проекциях –
- 27. КОНИЧЕСКИЕ ПРОЕКЦИИ косая коническая проекция – ось конуса располагается под углом к плоскости экватора. В косых
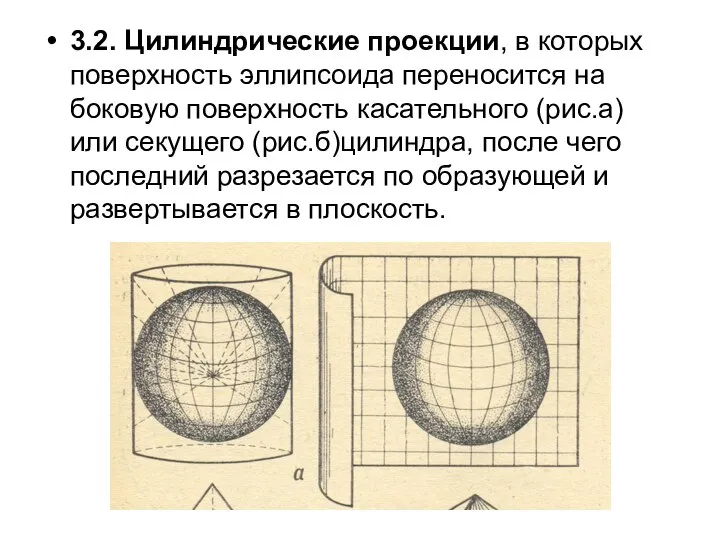
- 28. 3.2. Цилиндрические проекции, в которых поверхность эллипсоида переносится на боковую поверхность касательного (рис.а) или секущего (рис.б)цилиндра,
- 29. ВИДЫ ПРОЕКЦИЙ ПО ОРИЕНТИРОВКЕ ВСПОМОГАТЕЛЬНОЙ ПОВЕРХНОСТИ на примере цилиндрических проекций
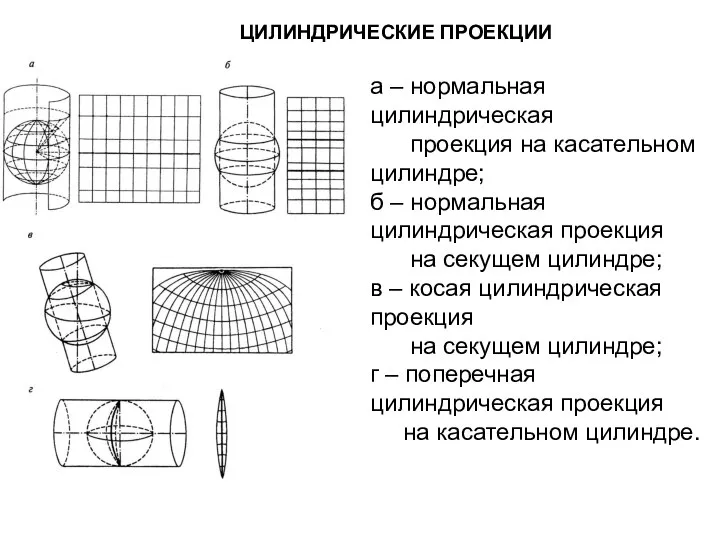
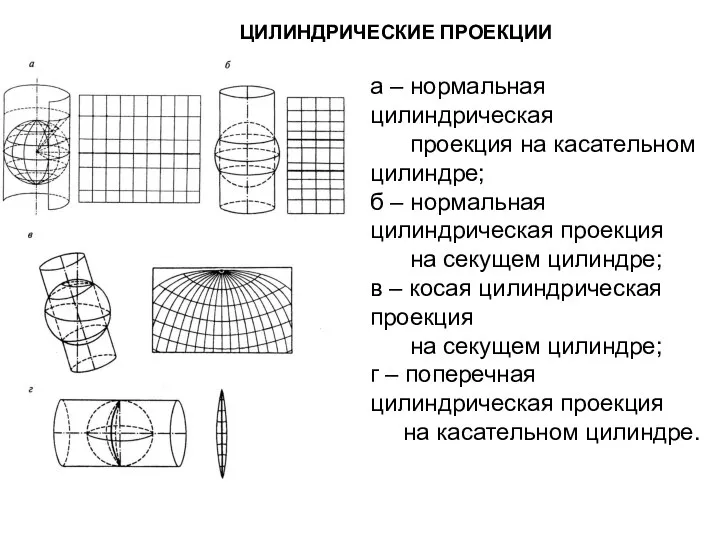
- 30. ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ а – нормальная цилиндрическая проекция на касательном цилиндре; б – нормальная цилиндрическая проекция на
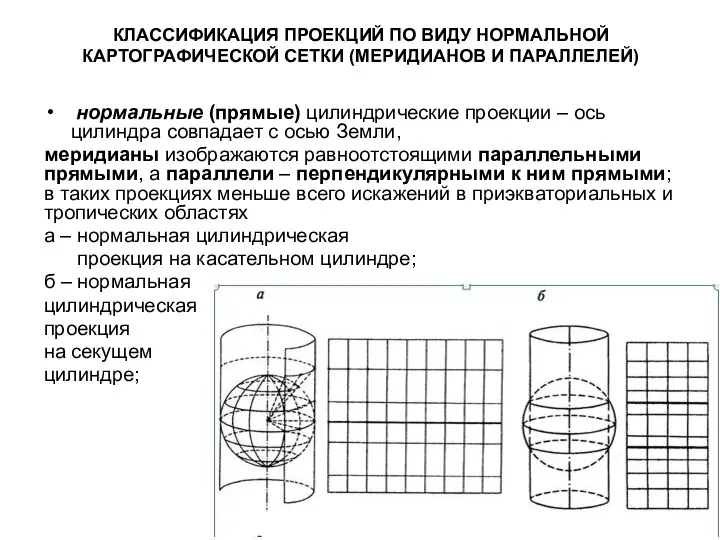
- 31. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) нормальные (прямые) цилиндрические проекции – ось
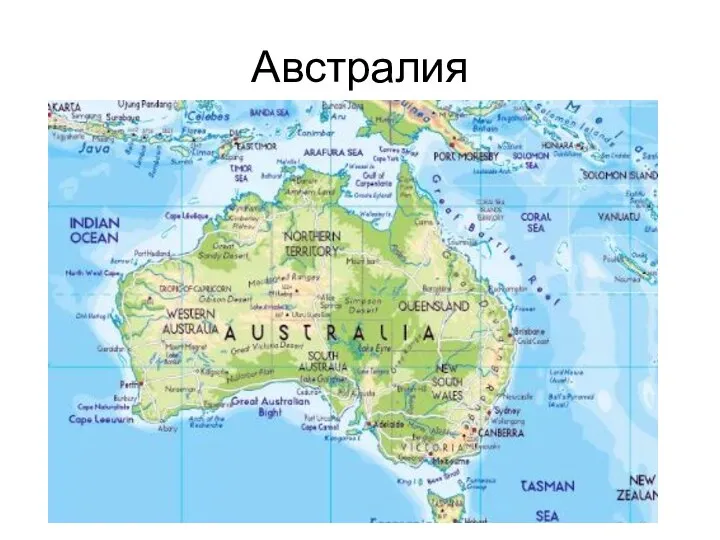
- 32. Австралия
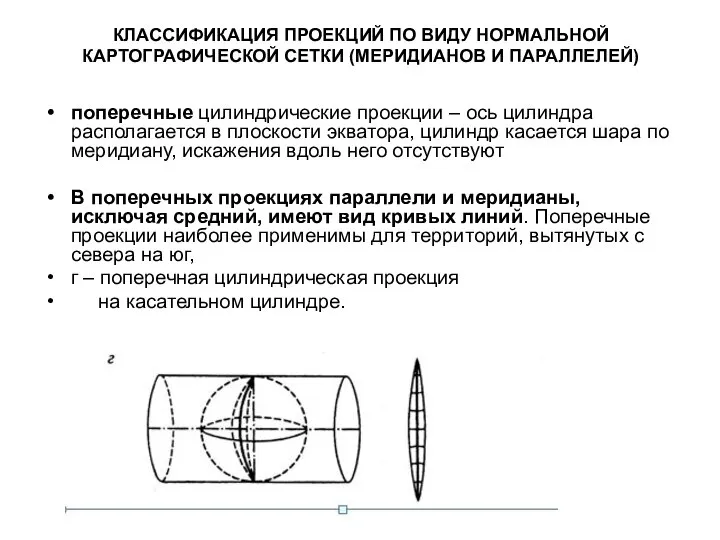
- 33. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) поперечные цилиндрические проекции – ось цилиндра
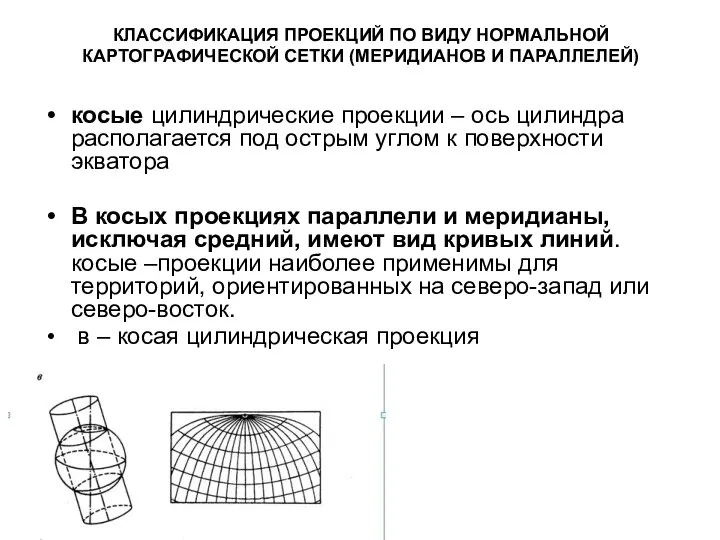
- 34. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) косые цилиндрические проекции – ось цилиндра
- 36. ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ а – нормальная цилиндрическая проекция на касательном цилиндре; б – нормальная цилиндрическая проекция на
- 37. Азимутальные проекции - когда проектирование эллипсоида осуществляется на касательную или секущую его плоскость. В этих проекциях
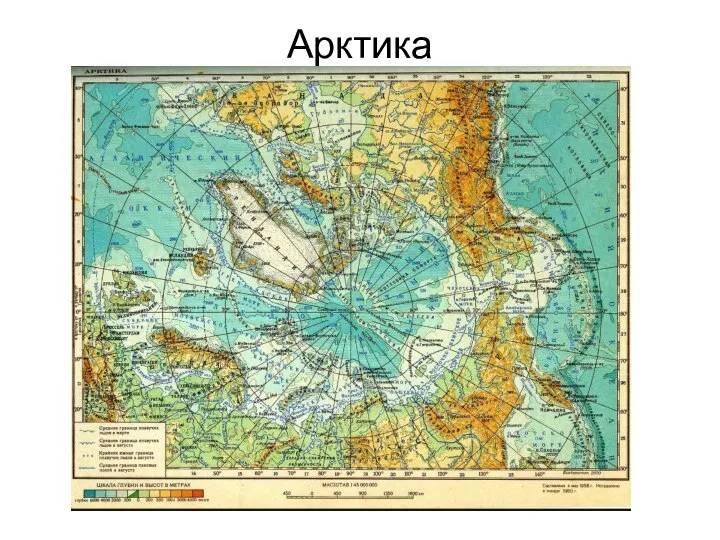
- 38. Арктика
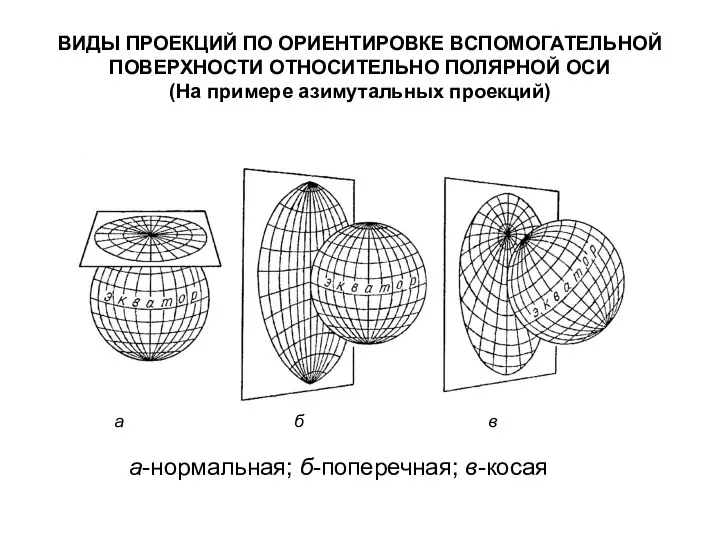
- 39. ВИДЫ ПРОЕКЦИЙ ПО ОРИЕНТИРОВКЕ ВСПОМОГАТЕЛЬНОЙ ПОВЕРХНОСТИ (На примере азимутальных проекций)
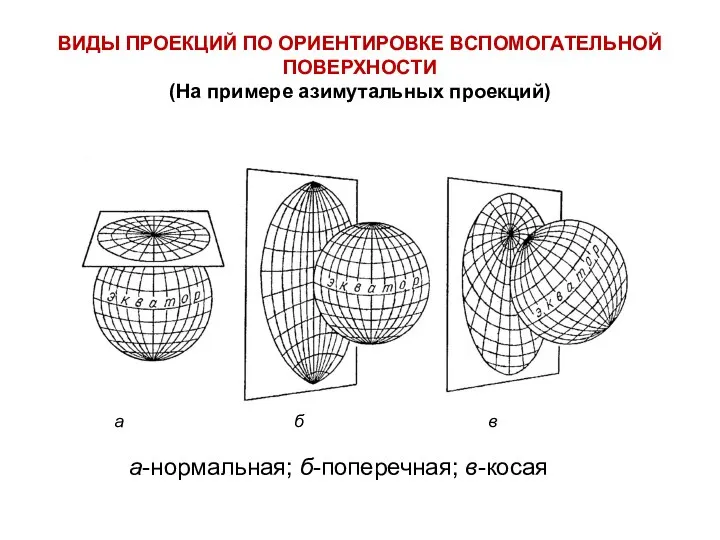
- 40. ВИДЫ ПРОЕКЦИЙ ПО ОРИЕНТИРОВКЕ ВСПОМОГАТЕЛЬНОЙ ПОВЕРХНОСТИ (На примере азимутальных проекций) а-нормальная; б-поперечная; в-косая а б в
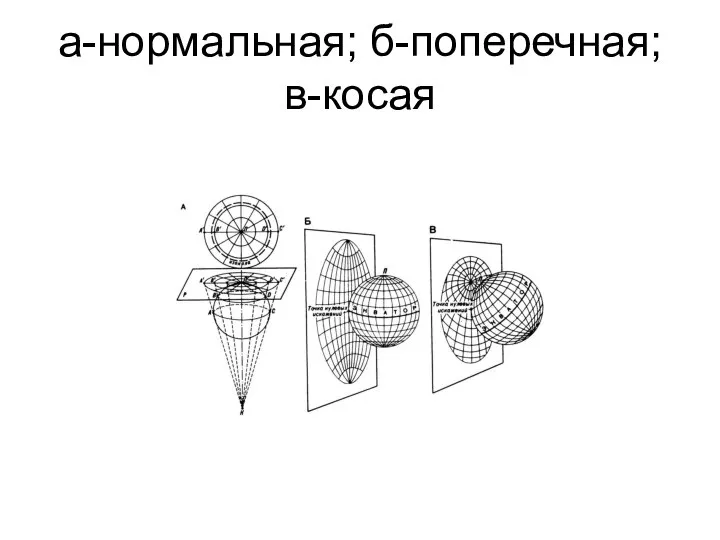
- 41. а-нормальная; б-поперечная; в-косая
- 43. В зависимости от расположения плоскости по отношению к земной оси азимутальные проекции бывают: А. нормальные (полярные,
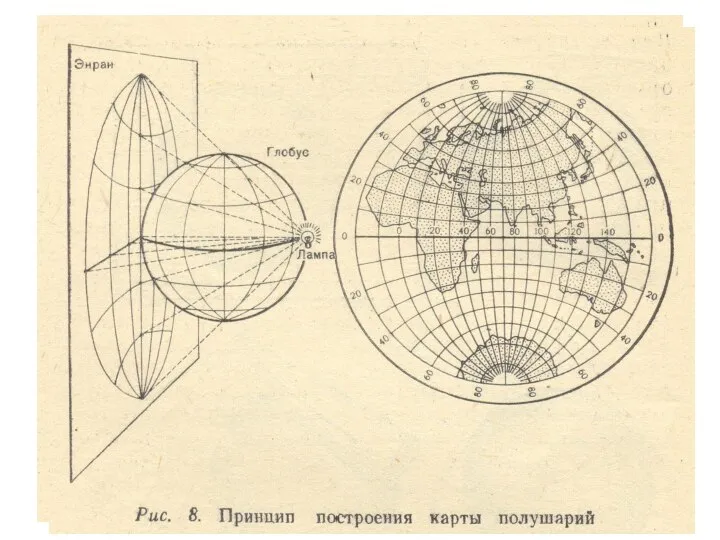
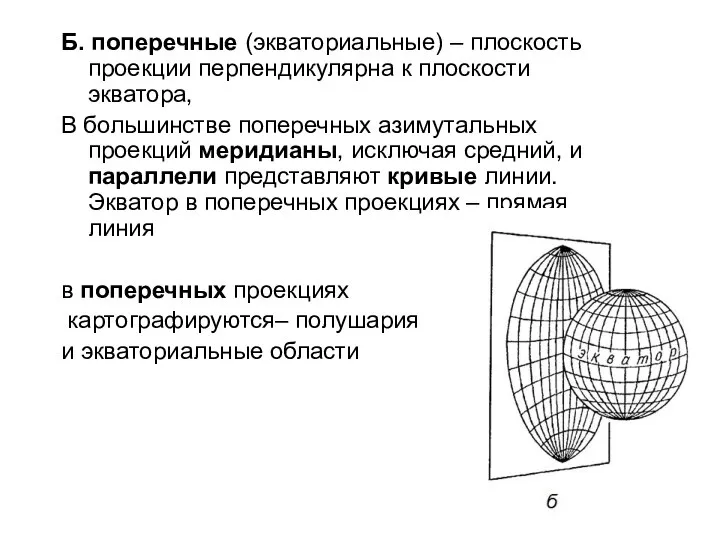
- 45. Б. поперечные (экваториальные) – плоскость проекции перпендикулярна к плоскости экватора, В большинстве поперечных азимутальных проекций меридианы,
- 46. ВИДЫ ПРОЕКЦИЙ ПО ОРИЕНТИРОВКЕ ВСПОМОГАТЕЛЬНОЙ ПОВЕРХНОСТИ ОТНОСИТЕЛЬНО ПОЛЯРНОЙ ОСИ (На примере азимутальных проекций) а-нормальная; б-поперечная; в-косая
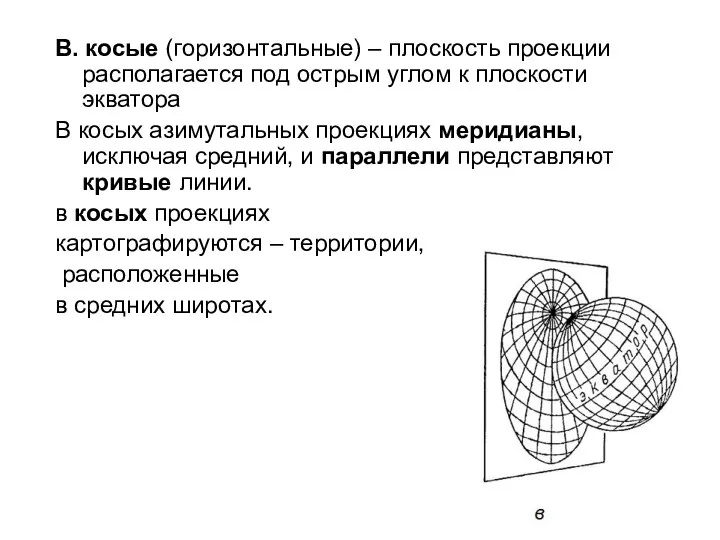
- 48. В. косые (горизонтальные) – плоскость проекции располагается под острым углом к плоскости экватора В косых азимутальных
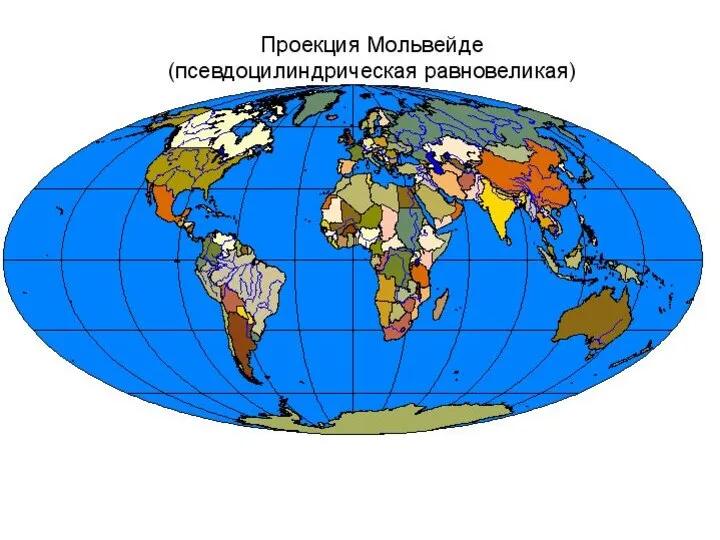
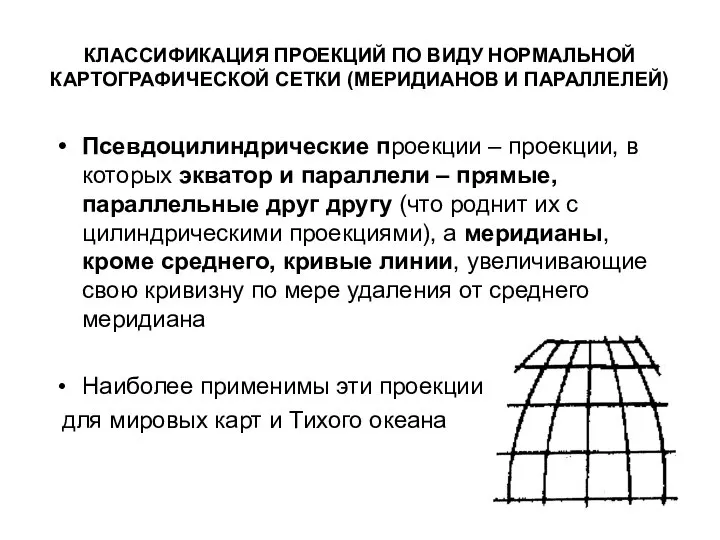
- 50. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) Псевдоцилиндрические проекции – проекции, в которых
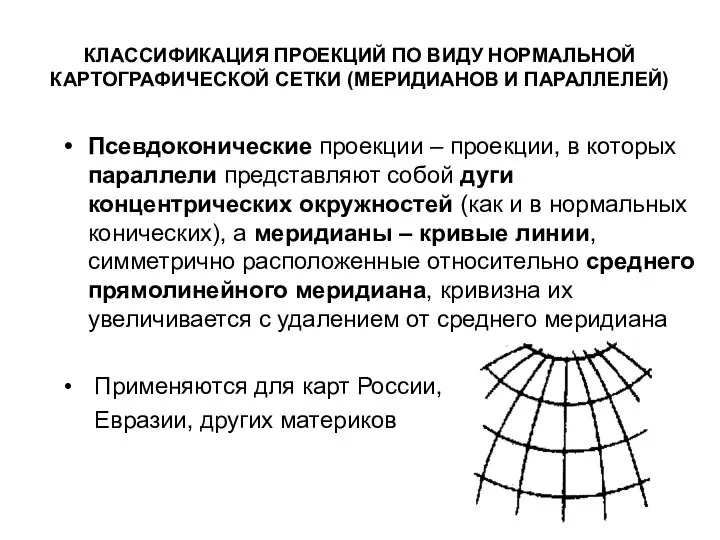
- 52. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) Псевдоконические проекции – проекции, в которых
- 55. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) Поликонические проекции – проекции, в которых
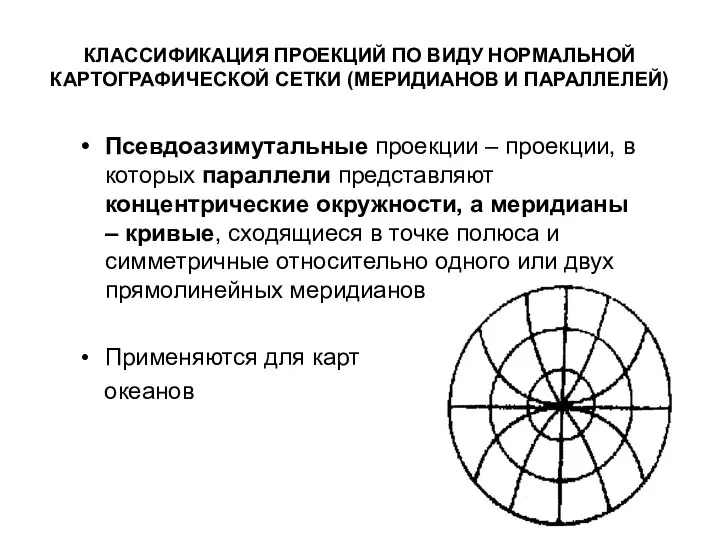
- 57. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) Псевдоазимутальные проекции – проекции, в которых
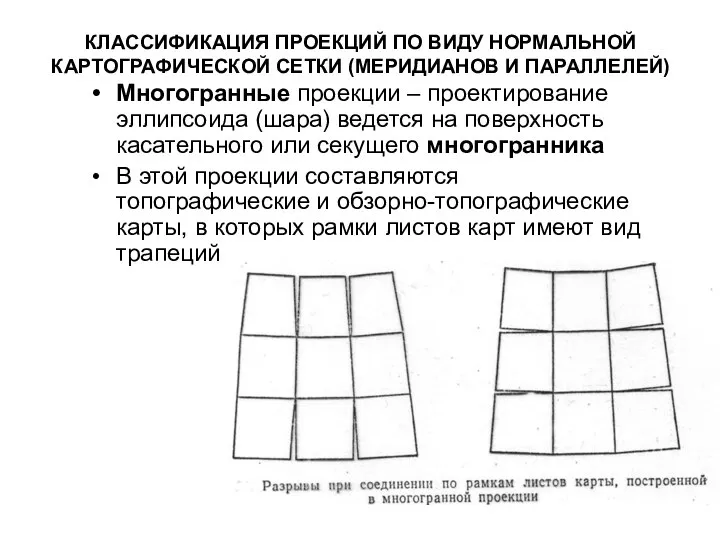
- 58. КЛАССИФИКАЦИЯ ПРОЕКЦИЙ ПО ВИДУ НОРМАЛЬНОЙ КАРТОГРАФИЧЕСКОЙ СЕТКИ (МЕРИДИАНОВ И ПАРАЛЛЕЛЕЙ) Многогранные проекции – проектирование эллипсоида (шара)
- 59. МНОГОГРАННЫЕ ПРОЕКЦИИ Разновидностью многогранных являются многополосные проекции. Полосы могут нарезать и по меридианам и по параллелям.
- 60. 4. Проекция Гаусса-Крюгера ПЗ При создании средне- и крупномасштабных тематических карт чаще всего используется равноугольная поперечно-цилиндрическая
- 61. История применения проекции Гаусса-Крюгера в нашей стране началась в 1928 году на эллипсоиде Бесселя для составления
- 62. В апреле 1946 г. Постановлением Правительства были утверждены новые исходные даты, характеризующие систему координат 1942 года,
- 63. С июля 2002 года в России в качестве Государственной принята система координат 1995 года (СК-95). в
- 64. В1825 г. Гаусс решил задачу по изображению одной поверхности на другой с сохранением углов, а в
- 65. В проекции Гаусса-Крюгера поверхность эллипсоида на плоскости отображается по меридиальным зонам, ширина которых равна 6 градусов.
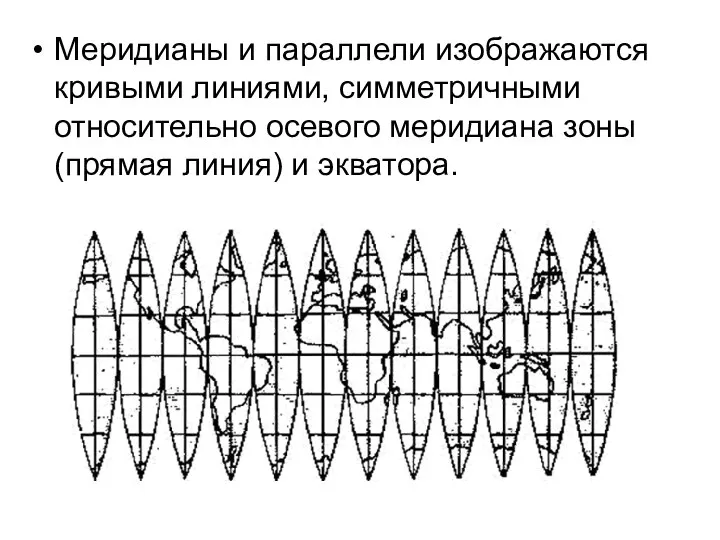
- 66. Меридианы и параллели изображаются кривыми линиями, симметричными относительно осевого меридиана зоны (прямая линия) и экватора.
- 67. Однако кривизна меридианов настолько мала, что западные и восточные рамки карты изображаются прямыми линиями. Параллели, совпадающие
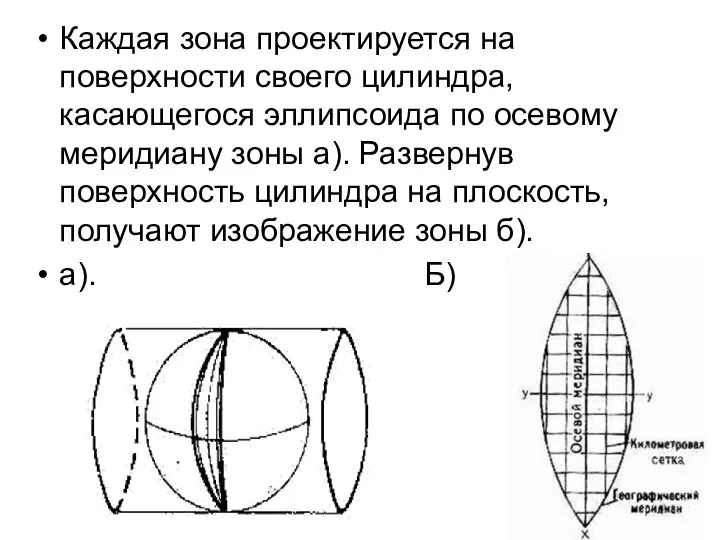
- 68. Каждая зона проектируется на поверхности своего цилиндра, касающегося эллипсоида по осевому меридиану зоны а). Развернув поверхность
- 69. В каждой зоне проекции Гаусса-Крюгера своя система координат: за ось Х (абцисса) принимают осевой меридиан зоны;
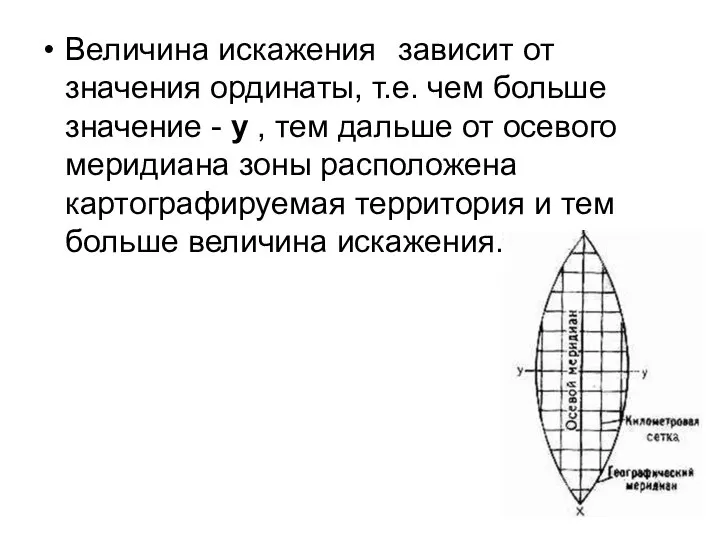
- 71. Величина искажения зависит от значения ординаты, т.е. чем больше значение - у , тем дальше от
- 73. Скачать презентацию




























 Камни Кабардино-Балкарии
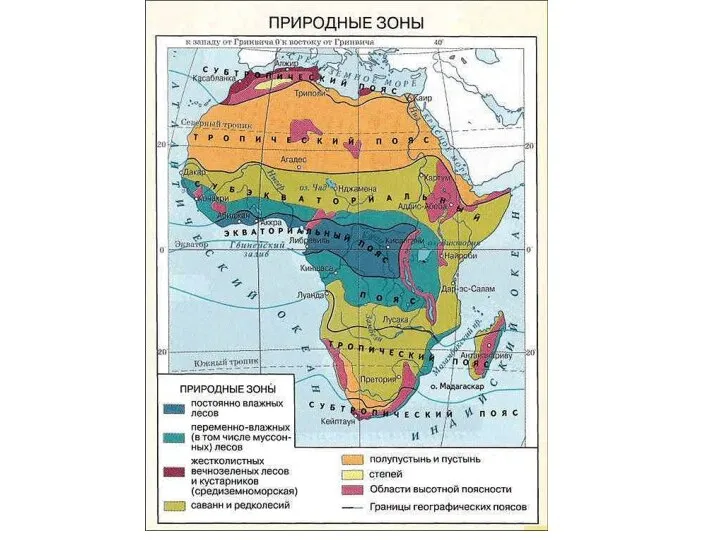
Камни Кабардино-Балкарии Природные зоны
Природные зоны Презентация на тему Ветер
Презентация на тему Ветер  Экологическая тропа Гарабаши: научно-познавательная экскурсия
Экологическая тропа Гарабаши: научно-познавательная экскурсия 20141124_afrika
20141124_afrika Презентация на тему Национальные парки Африки
Презентация на тему Национальные парки Африки  Презентация на тему Практические работы как один из способов формирования географических знаний
Презентация на тему Практические работы как один из способов формирования географических знаний  Köln
Köln Людзі зямлі беларускай
Людзі зямлі беларускай Аэрологические оптические шар-пилотные наблюдения
Аэрологические оптические шар-пилотные наблюдения Географическая оболочка Земли. Свойства географической оболочки. 6 класс
Географическая оболочка Земли. Свойства географической оболочки. 6 класс Леса умеренного пояса. 2-й класс
Леса умеренного пояса. 2-й класс Карлутская площадь или сквер у вечного огня. Ижевск
Карлутская площадь или сквер у вечного огня. Ижевск Землетрясения. Очаг, эпицентр
Землетрясения. Очаг, эпицентр 1_ Преобразование рельефа в результате хозяйственн
1_ Преобразование рельефа в результате хозяйственн Римская республика
Римская республика Краеведческая игра Путешествие куропаток по Курскому краю
Краеведческая игра Путешествие куропаток по Курскому краю Рельеф дна Мирового океана
Рельеф дна Мирового океана 20170503_priroda_rossii
20170503_priroda_rossii Обобщение темы Страны Африки
Обобщение темы Страны Африки Дарвинский государственный природный биосферный заповедник
Дарвинский государственный природный биосферный заповедник Презентация на тему Горючие полезные ископаемые
Презентация на тему Горючие полезные ископаемые  Путешествие по Транссибирской железной дороге из Москвы во Владивосток
Путешествие по Транссибирской железной дороге из Москвы во Владивосток Западно-Сибирская равнина
Западно-Сибирская равнина Биос мой
Биос мой Путешественники
Путешественники План туризма Воронежской области
План туризма Воронежской области Дальний Восток
Дальний Восток