Содержание
- 2. Количественная оценка движения подземных вод в естественных условиях безнапорного водоносного горизонта Расход фильтрационного потока Единичный расход
- 3. Расчётная схема безнапорного водоносного горизонта на горизонтальном водоупоре Безнапорный водоносный горизонт на горизонтальном водоупоре
- 4. Равномерные и неравномерные фильтрационные потоки Естественные фильтрационные потоки
- 5. Равномерным называется такой фильтрационный поток, параметры которого не изменяются в пространстве Естественные фильтрационные потоки Параметры потока:
- 6. Покажем каким является однородный напорный водоносный горизонт постоянной мощности Естественные фильтрационные потоки
- 7. Проанализируем изменение параметров однородного фильтрационного потока напорного водоносного горизонта постоянной мощности в пространстве Для анализа разделим
- 8. Сравним между собой выделенные фрагменты (I, II, III, IV) напорного водоносного горизонта Естественные фильтрационные потоки
- 9. m1=m2=m3=m4 k1=k2=k3=k4 l1=l2=l3=l4 Естественные фильтрационные потоки Мощности водоносного горизонта, коэффициенты фильтрации и размеры выделенных фрагментов одинаковы
- 10. m1=m2=m3=m4 k1=k2=k3=k4 l1=l2=l3=l4 Естественные фильтрационные потоки Сравнение показывает равенство мощности и коэффициента фильтрации в границах одинаковых
- 11. Естественные фильтрационные потоки Обратимся к анализу величины единичного расхода в выделенных фрагментах (I, II, III, IV)
- 12. Естественные фильтрационные потоки Такое представление фундаментальной зависимости позволяет наглядно связать величину фильтрационного сопротивления с разницей напоров
- 13. Естественные фильтрационные потоки Можно утверждать, что в области фильтрации падение напора затрачивается на преодоление фильтрационного сопротивления,
- 14. Естественные фильтрационные потоки Для наглядности можно представить, что сопротивление потоку обратно пропорционально его сечению. На рисунке
- 15. Естественные фильтрационные потоки Сравнение показывает равенство фильтрационных сопротивлений фрагментов (I, II, III, IV) напорного водоносного горизонта
- 16. Естественные фильтрационные потоки На преодоление одинаковых фильтрационных сопротивлений затрачиваются одинаковые разности напоров в пределах каждого из
- 17. Естественные фильтрационные потоки Напорный водоносный горизонт постоянной мощности и однородный по фильтрационным свойствам обладает равномерным фильтрационным
- 18. Естественные фильтрационные потоки Повторим анализ для однородного безнапорного водоносного горизонта на горизонтальном водоупоре
- 19. Для анализа разделим область фильтрации безнапорного водоносного горизонта на одинаковые по длине фрагменты Естественные фильтрационные потоки
- 20. Вспомним, что по закону Дарси скорость фильтрации связывается с изменением (падением напора). Это значит, что по
- 21. На преодоление большей величины фильтрационного сопротивления затрачивается большая разность напоров Естественные фильтрационные потоки Малые катеты криволинейных
- 22. Естественные фильтрационные потоки Безнапорный однородный водоносный горизонт обладает неравномерным фильтрационным потоком, как следствие депрессионная кривая в
- 23. Пример расчёта: График депрессионной кривой неоднородного напорного водоносного горизонта L_1 100 L_2 100 L_3 100 q
- 24. Пример расчёта: График депрессионной кривой неоднородного напорного водоносного горизонта Параметры Неоднородного НВГ: Мощность напорного водоносного горизонта
- 25. Пример расчёта: График депрессионной кривой неоднородного напорного водоносного горизонта Параметры Неоднородного НВГ: Мощность напорного водоносного горизонта
- 26. Пример расчёта: График депрессионной кривой неоднородного напорного водоносного горизонта Параметры Неоднородного НВГ: Мощность в средней части
- 27. Карта гироизогипс даёт полное представление о структуре фильтрационного потока, включая его локальные направления и скорости (на
- 28. Гидродинамической сеткой фильтрационного потока называется совокупность взаимно ортогональных линий тока и линий равных напоров. Гидродинамическая сетка
- 29. Естественные фильтрационные потоки Пример гидродинамической сетки (б) и гидрогеологический разрез (а) 1-граница выхода коренных пород; 2-почвенный
- 31. Скачать презентацию

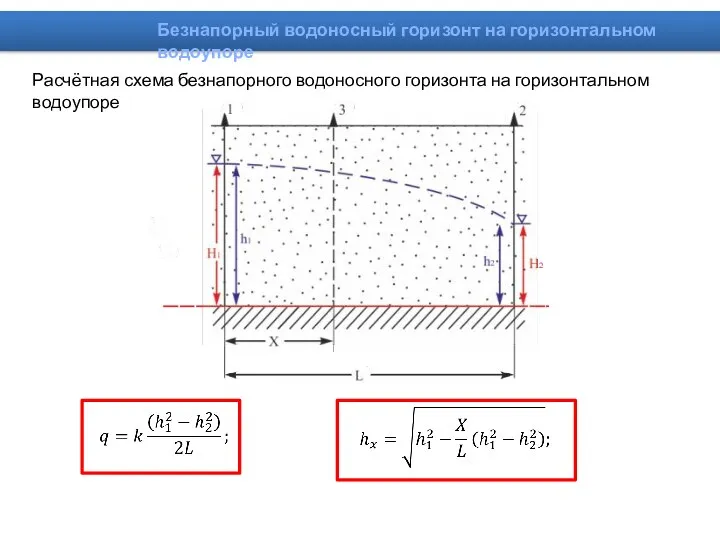

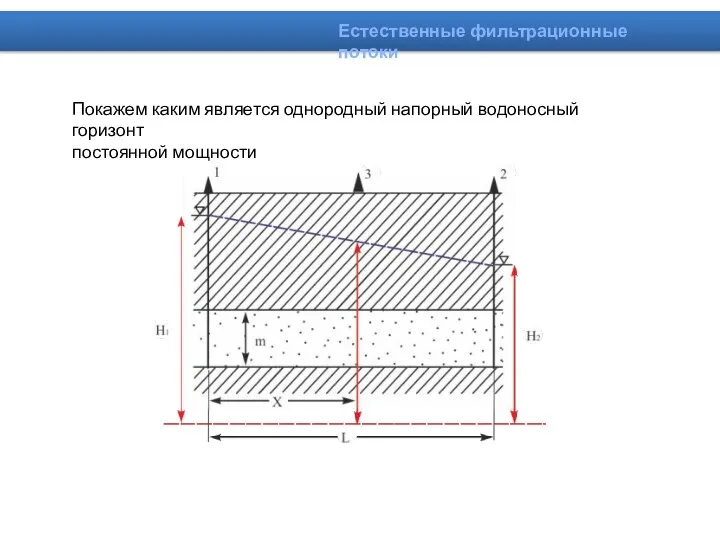

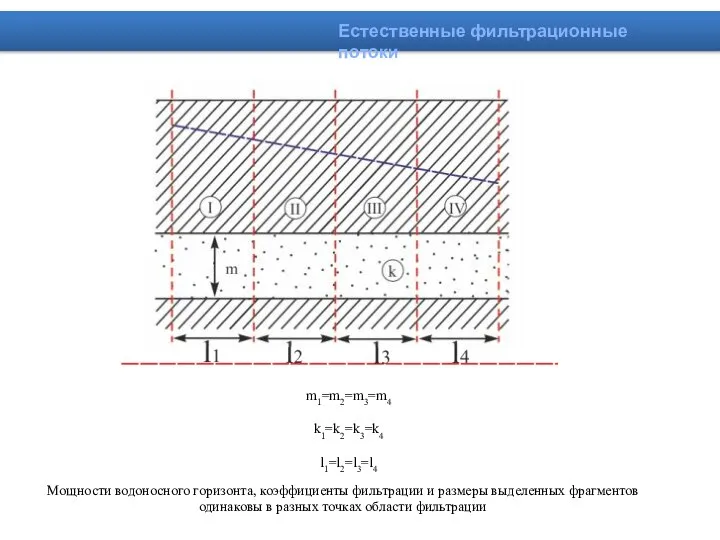
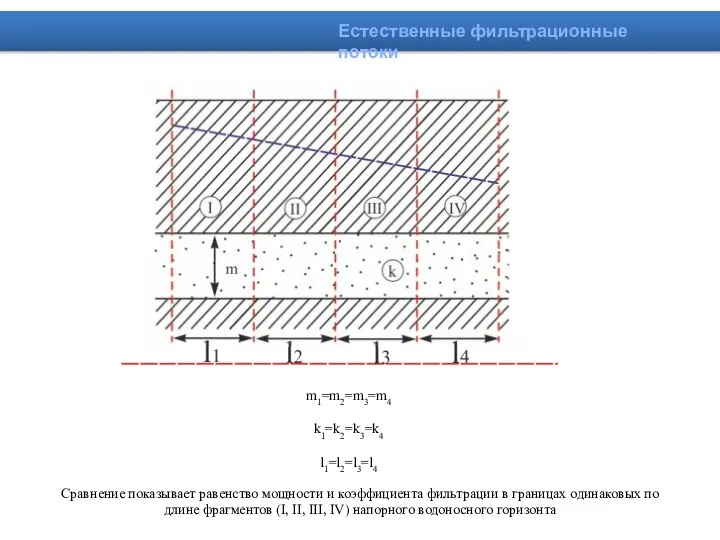



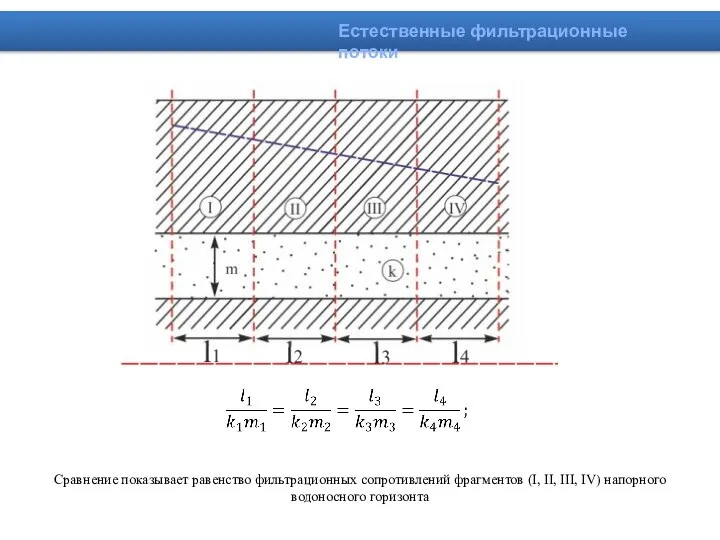
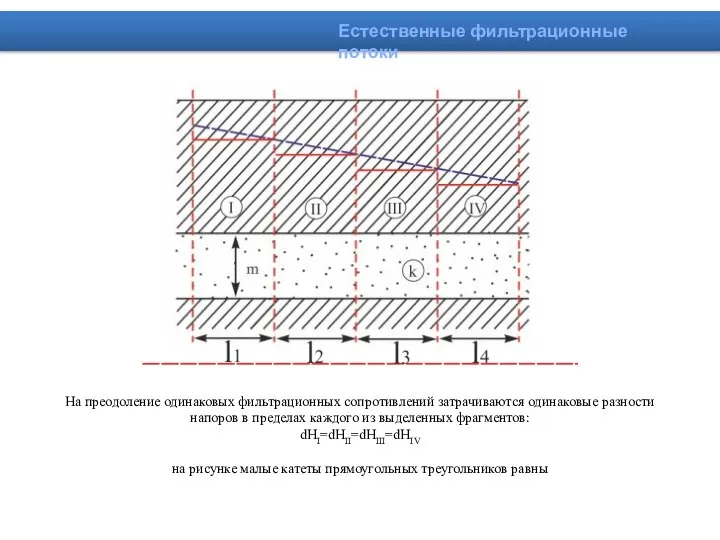
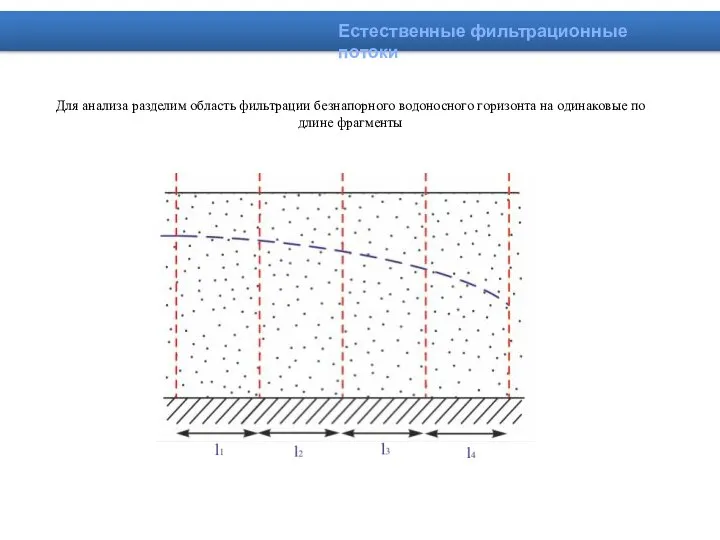
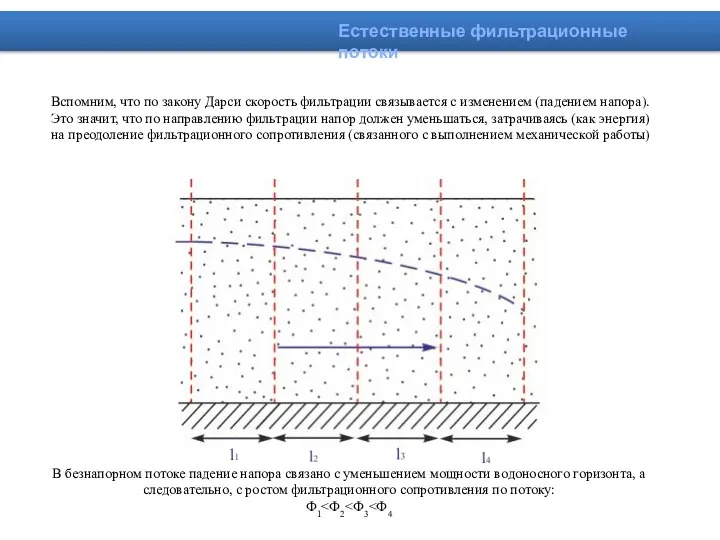
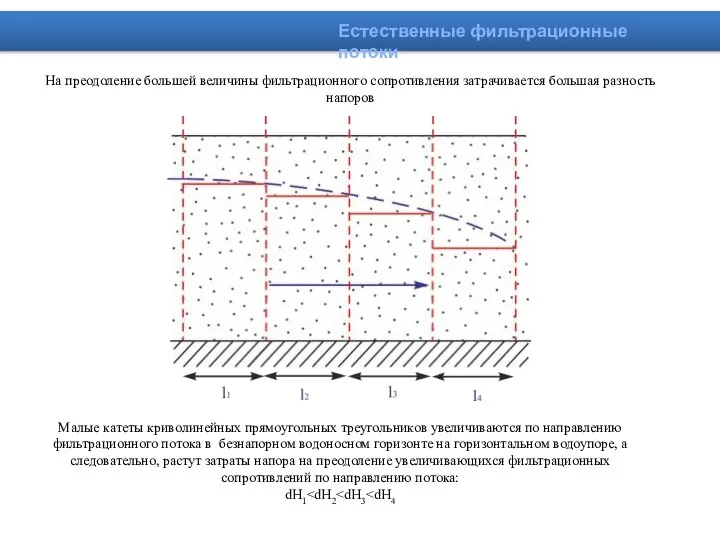
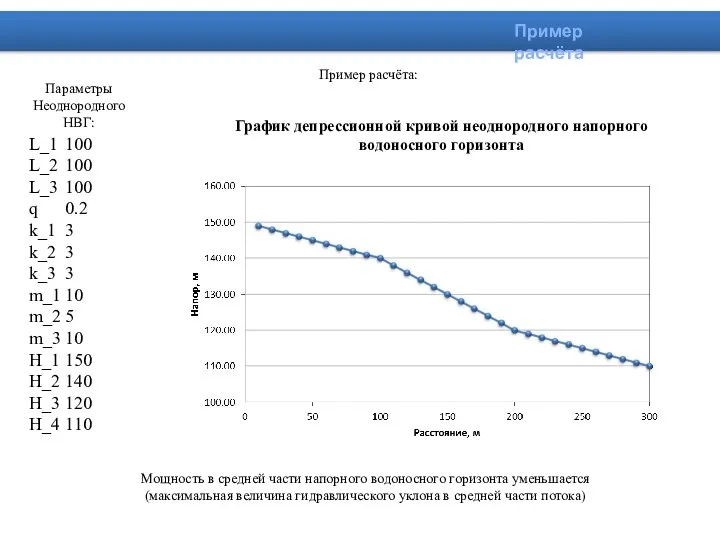
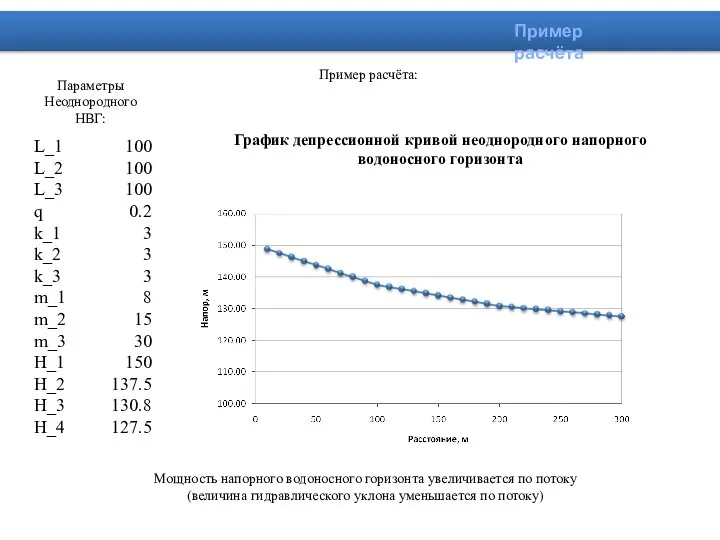
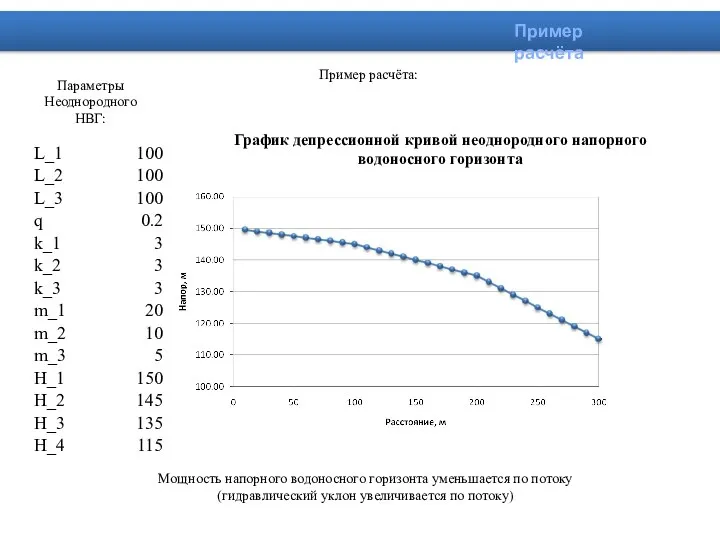
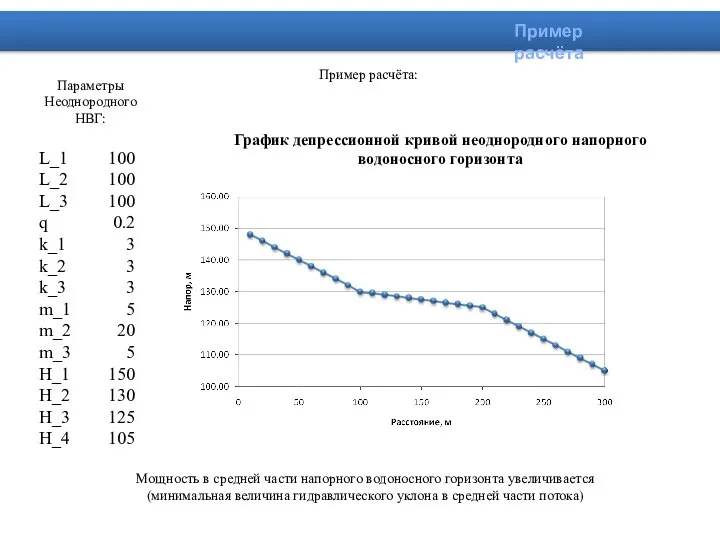
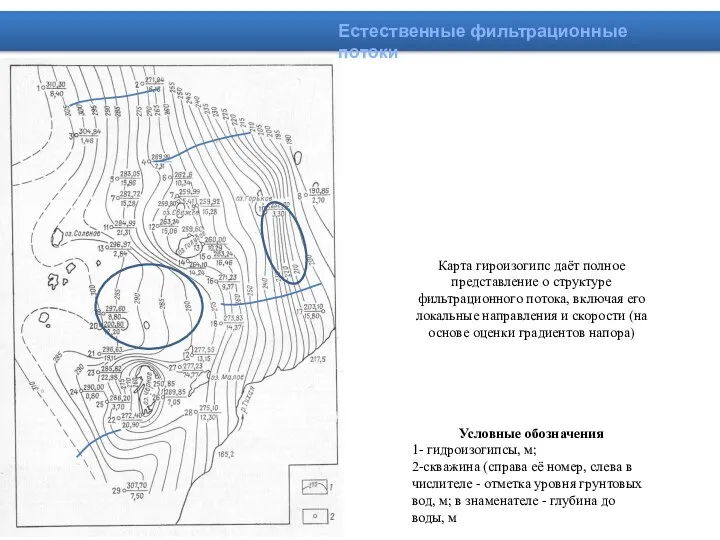

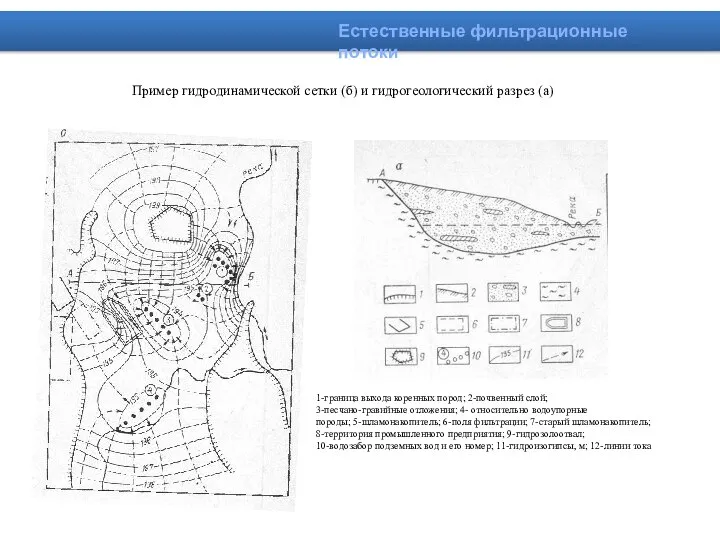
 Схема ділянки Бородинське
Схема ділянки Бородинське Презентация на тему Проблемы мирового океана (10 класс)
Презентация на тему Проблемы мирового океана (10 класс)  Город Сысерть
Город Сысерть Почвенные ресурсы России
Почвенные ресурсы России Остров Мадагаскар
Остров Мадагаскар Объединение Юные туристы. Повторение пройденного материала
Объединение Юные туристы. Повторение пройденного материала Мой город Санкт-Петербург
Мой город Санкт-Петербург Рельеф - тектоническая основа
Рельеф - тектоническая основа Проверка знаний по теме Гидросфера
Проверка знаний по теме Гидросфера Der Gutshof Sergievka
Der Gutshof Sergievka Географическая разминка
Географическая разминка Ресурсообеспеченность
Ресурсообеспеченность Стороны горизонта. Ориентирование на местности
Стороны горизонта. Ориентирование на местности Эксперименты на уроках географии
Эксперименты на уроках географии Köküň görnüşleri
Köküň görnüşleri Wellington - New Zealand capital
Wellington - New Zealand capital Один день из жизни Робинзона Крузо!
Один день из жизни Робинзона Крузо! Концептуальный пилотный проект. Биосферная территория опережающего развития
Концептуальный пилотный проект. Биосферная территория опережающего развития Состав и строение литосферы
Состав и строение литосферы Муниципальное образование Белоглинский район
Муниципальное образование Белоглинский район Таиланд. Город Патайя
Таиланд. Город Патайя Самоанцы — байырғы халық аралдары Самоа
Самоанцы — байырғы халық аралдары Самоа Секция «Краеведение и туризм » «Изучение топонимов Дона – названий городов Ростовской области» Работу выполнила: Заболотнева В
Секция «Краеведение и туризм » «Изучение топонимов Дона – названий городов Ростовской области» Работу выполнила: Заболотнева В Презентация на тему Баргузинский заповедник
Презентация на тему Баргузинский заповедник  Строение и морфологические признаки почв
Строение и морфологические признаки почв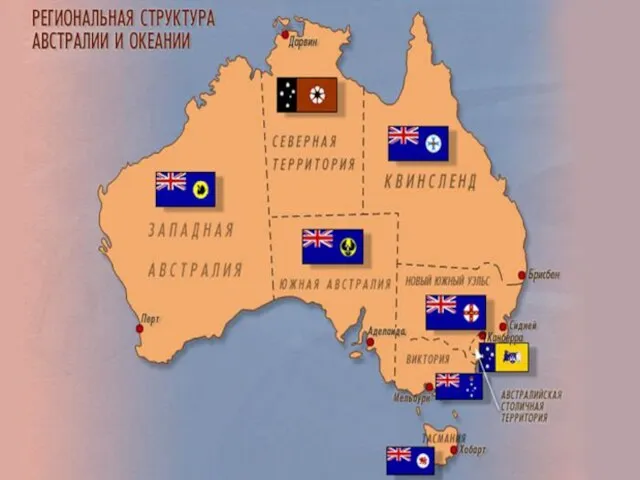 Презентация на тему Урок брейн-ринг на тему Австралия и Океания
Презентация на тему Урок брейн-ринг на тему Австралия и Океания  Презентация на тему Дальний Восток России
Презентация на тему Дальний Восток России  Албания
Албания