Презентация по географии на тему _Карта и её матем

Вы узнаете:
1. Что такое картографическая проекция.
2. Какие существуют виды картографических проекций.
3. Почему на географической карте возникают искажения изображения земной поверхности.

Географическая карта — изображение модели земной поверхности, содержащее координатную сетку с условными знаками на плоскости в уменьшенном виде.

Карта
Карта — математически определённая образно-знаковая модель действительности.
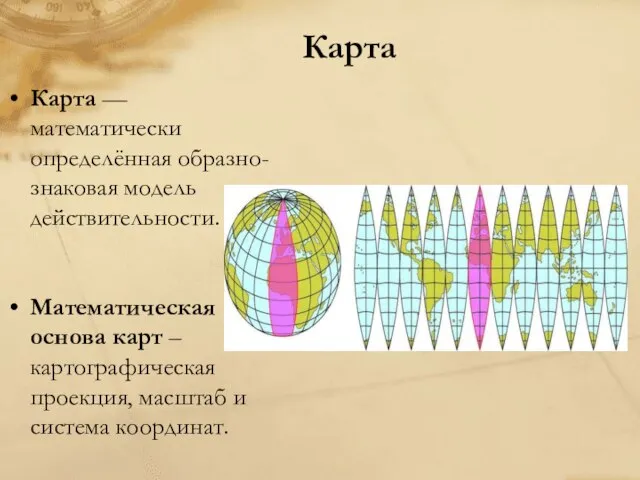
Математическая основа карт – картографическая проекция, масштаб и система координат.

Картографические проекции
Картографическая проекция — математически определенный способ отображения поверхности Земли на плоскость.
Суть проекций связана с тем, что фигуру Земли , не развертываемую в плоскость, заменяют на другую фигуру, развёртываемую на плоскость.

Картографические искажения
Искажение длин — базовое искажение. Остальные искажения из него логически вытекают. Проявляется в изменении масштаба.
Искажения площадей логически вытекают из искажения длин. За характеристику искажения площадей принимают отклонение площади эллипса искажений от исходной площади на эллипсоиде.
Искажения углов логически вытекают из искажения длин. За характеристику искажений углов на карте принимают разность углов между направлениями на карте и соответствующими направлениями на поверхности эллипсоида.
Искажения формы — графическое изображение вытянутости эллипсоида.

По характеру искажений:
Равноугольные проекции — проекции без искажений углов. Весьма удобны для решения навигационных задач. Масштаб зависит только от положения точки и не зависит от направления. Угол на местности всегда равен углу на карте, линия, прямая на местности — прямая на карте.

Равновеликие проекции
В равновеликих проекциях отсутствуют искажения площадей, но при этом сильны искажения углов и форм, (материки в высоких широтах сплющиваются). В такой проекции изображаются экономические, почвенные и другие мелкомасштабные карты.

Произвольные проекции
В произвольных проекциях имеются искажения и углов, и площадей, но в значительно меньшей степени, чем в равновеликих и равноугольных проекциях, поэтому они наиболее употребляемые.

Виды проекций по типу вспомогательной поверхности

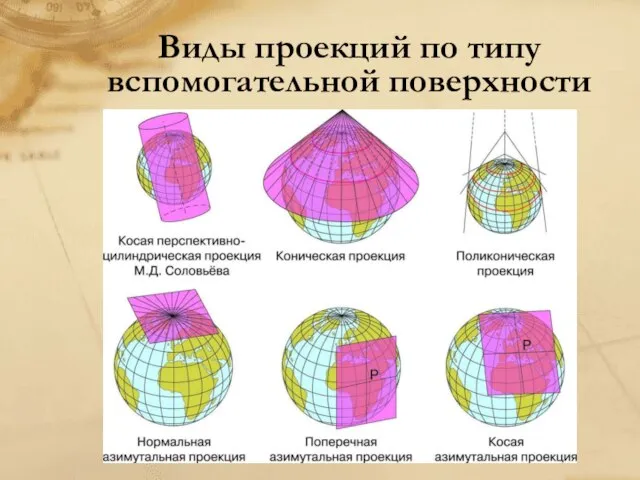
Азимутальная проекция
Вспомогательная поверхность – плоскость.
В нормальных азимутальных проекциях параллели изображаются концентрическими окружностями, а меридианы — пучком прямых, исходящих из центра.
Меридианы и параллели в косых и поперечных азимутальных проекциях изображаются кривыми линиями, за исключением среднего меридиана, на котором находится центральная точка проекции. В поперечных проекциях прямой изображается также экватор.

Цилиндрические проекции
Вспомогательная поверхность – цилиндр.
В прямых цилиндрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг другу.
В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.

Конические проекции
Вспомогательная поверхность – конус.
В конической проекции изображение строится на боковой поверхности конуса, секущего земной шар по двум параллелям или касательного к нему. Вершина конуса лежит на продолжении земной оси.
Параллели нормальной сетки являются дугами концентрических окружностей, а меридианы — их радиусами, углы между которыми пропорциональны соответствующим разностям долгот.