Корреляционный анализ

План
Понятие корреляционной связи
Виды корреляционных коэффициентов баз данных

Литература
Абрамов В.К. Корреляционный анализ в исторических исследованиях. Саранск, 1990.
Мазур Л.Н. Методы исторического исследования. Екатеринбург, 2011.
Миронов Б.Н. История в цифрах. Л, 1991.

Причины использования метода в исторических исследованиях
Изучая историю, нетрудно заметить, что существует взаимосвязь явлений и процессов, происходящих в природе и обществе, внутри общества, во времени и пространстве.
Оценка исторического факта предполагает выявление факторов способствовавших и препятствовавших его появлению,
а их оценка в историческом исследовании чаще всего бывает расплывчатой.
Читаем -"сильное влияние...", "решающее значение..","определенное воздействие…." и т.п.

Причины использования метода в исторических исследованиях
Внести количественную определенность помогает корреляционная связь,
направленная на определение тесноты взаимосвязи признаков и степени воздействия различных факторов на изучаемый объект.
Констатировать наличие связи между признаками позволяют аналитические группировки,
Но:
они не дают возможность количественно выразить силу взаимодействия одного признака с другим (парная корреляция)
или же с совокупностью признаков (множественная корреляция).

Причины использования метода в исторических исследованиях
Все связи, которые могут быть измерены, можно считать статистическими,
частным случаем которых являются функциональные (жестко детерминированные).
Они возможны при условии, что на один из двух рассматриваемых признаков влияет только второй признак этой же пары и ничто больше.
В реальной природе, а тем более в общественной жизни таких связей нет.
На каждый исторический факт одновременно воздействует множество причин.

Термин корреляция
употребляется в науке с конца XYIII века.
Его ввел французский палеонтолог Жорж Кювье,
основавший "закон корреляции",
согласно которому череп с рогами обязательно принадлежал травоядному животному, обладавшему копытными конечностями;
если же лапа имела когти, то животное
было хищным, без рогов, но с крупными клыками.

Термин корреляция
Об этом законе сохранился рассказ о неудачной шутке студентов, пытавшихся во время университетского карнавала напугать Кювье.
Ряженный в шкуре и маске с рогами крикнул профессору: "Я тебя съем!"
На что получил спокойный ответ, что рогатых хищников не бывает,
а за незнание закона корреляции можно получить плохую оценку.

Термин корреляция
Это систематическая и обусловленная связь между двумя рядами данных
Или связь переменных, при которой одному значению признака соответствует несколько значений другого признака

Корреляционная связь
Характеризует сложный механизм взаимодействия двух или нескольких признаков
При котором при изменении одного признака случайные варианты второго признака закономерно изменяются
И величина значений второго признака зависит от величины первого
(например, связь между ростом и весом человека;
посевной площадью и валовым сбором зерна,
понижением жизненного уровня и революционной активностью т.п.)

Идея метода
Идея сопоставления колебаний значений признака относительно друг друга
Если численные значения одного признака изменяются одновременно со значением другого, то можно предположить, что между ними существует связь
Следовательно, метод позволяет приблизиться к пониманию причинно-следственных связей

Пути возникновения корреляционной связи
Причинная зависимость предполагает, что один из пары рассматриваемых признаков выступает как фактор,
второй - как результат.
Например, качество почвы может рассматриваться фактором урожайности сельскохозяйственных культур.

Пути возникновения корреляционной связи
Существует корреляционная связь и между двумя следствиями одной причины.
Пример такой связи приводил крупнейший российский статистик начала XX в. Александр Александрович Чупров.
Рассматривались два признака –
количество пожарных команд в городе и
размер ущерба, причиненного городу от пожаров.
Выходило,
что, чем больше в городе пожарных, тем больше убытков от
пожаров.
Встал вопрос - не сократить ли пожарные команды?

Пути возникновения корреляционной связи
В данном случае мы имеем дело не с причиной и следствием,
а с двумя следствиями общей причины - размером города.
Логично, что в крупных городах больше штат пожарных, т.к. чаще возникают пожары и ущерб огнем причиняется значительный.

Пути возникновения корреляционной связи
Сложнее дело обстоит тогда, когда каждый из признаков
является одновременно и причиной, и следствием.
Здесь мы сталкиваемся со взаимосвязью, взаимозависимостью между признаками.
Например, размер оплаты труда зависит от его производительности,
но, в то же время, выступает в качестве стимула, а
значит, фактора повышения уровня производительности труда.

Условия применения корреляционного анализа
1. Необходимо достаточное количество наблюдений для изучения.
На практике считается, что число наблюдений должно не менее чем в 5–6 раз превышать число факторов
(также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов).

Условия применения корреляционного анализа
2. Исходная совокупность значений должна быть качественно однородной.
3. Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой,
а не наблюдается действие третьего фактора.

Методика метода
Прежде, чем приступать непосредственно к корреляционному анализу,
надо проверить правомерность его применения,
надо проверить, будут ли его результаты реально отражать историческую картину.

Методика метода
Признаки, исследуемые методом корреляции, должны быть нормально распределены и линейно зависимы между собой.
Признак обладает свойством нормальности, если его
значения симметрично распределяются от "центра",
которым считается его средняя арифметическая величина.

Методика метода
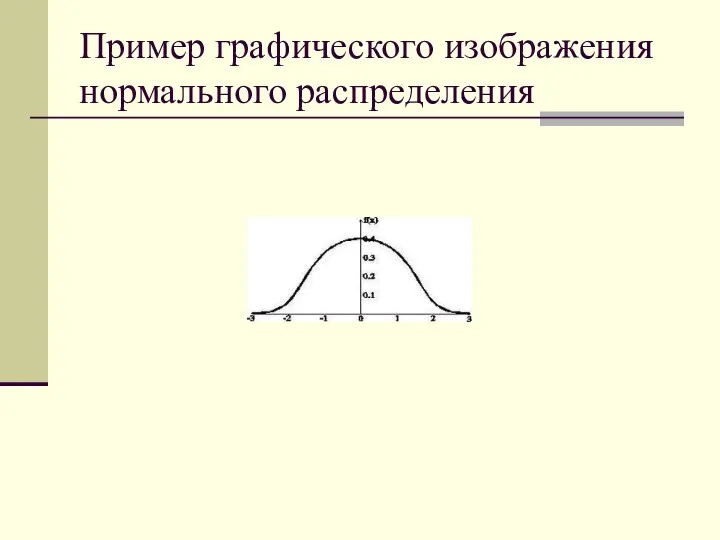
Проще всего проверить нормальность распределения графическим методом.
График нормально распределенного признака имеет колоколообразный вид с центром, совпадающим со значением средней арифметической

Пример графического изображения нормального распределения

Нормальное распределение в социальных науках
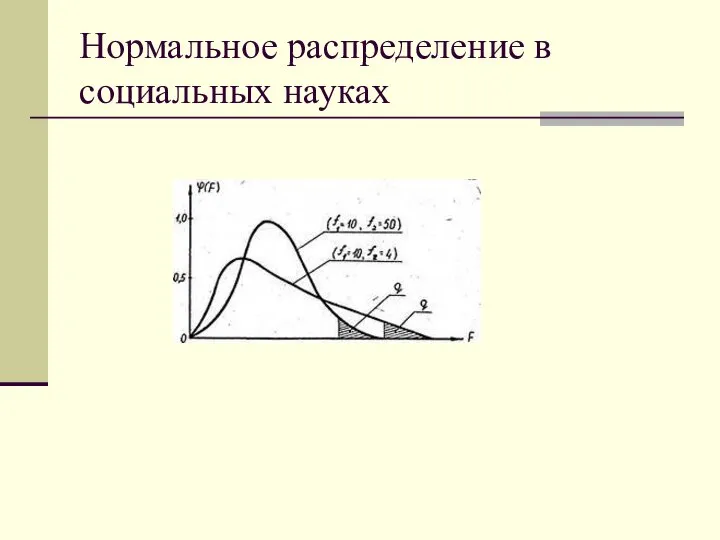
В истории среди признаков, характеризующих развитие общества, нет строгой нормальности распределения.
Практика использования математических методов в общественных науках доказала целесообразность относить к нормальным распределения с незначительно нарушенной симметрией,
с перекосами в ту или иную сторону, с центром, совпадающим не со значением средней
арифметической,
а перенесенным в максимальное значение признака.
К нормальным можно причислять и графики V-образной
формы и "опрокинутые колоколы".

Нормальное распределение в социальных науках

Методика метода
Свойство линейности в изучении взаимосвязи признаков
также служит необходимым предварительным условием использования многих математических методов.
Линейная зависимость между двумя признаками характеризуется условием,
при котором с увлечением на единицу значений одного признака изменяются в ту или иную сторону значения второго.

Методика метода
Проверка формы зависимости проводится с помощью графического метода.
В системе координат двух признаков точками
отмечаются имеющиеся данные.
Если пространство точек имеет вид прямой линии, то можно эту зависимость характеризовать как линейную, независимо от направления точечного скопления.

Проверка формы зависимости проводится с помощью графического метода

Методика метода
Так же, как и нормальности, строгой линейности в истории не существует. Достаточно приближенного выполнения данного свойства без привлечения более сложных специальных методик.

Методика метода
1. Проверка нормальности и линейности должна обязательно проводиться перед применением математических методов.
От этого зависит степень исторической достоверности результатов математических вычислений.
2. Свойства нормальности и линейности выясняются по
несгруппированным данным.

Методика метода
3. Нормальность и линейность определяются относительно каждого признака изучаемого явления.
4. Если признаки не отвечают свойствам нормальности и линейности - это еще не означает отказа от применения математико-статистических методов.
Разработан ряд приемов, преобразующих значения признаков, существенно отклоняющихся от указанных свойств.

Выбор формулы корреляции
Зависит:
От характера исходных данных,
от особенностей источника
и задач исследования

формулы корреляции
Чаще всего при изучении массовых источников применяют
коэффициент линейной корреляции (r).
Он вычисляется по
формуле:

коэффициент линейной корреляции
X и y - значения рассматриваемых признаков;
Х и Y- средние арифметические величины признаков;
п - общее число наблюдений

Пример коэффициента линейной корреляции (r)
рассмотрим по данным о возрасте и количестве детей двадцати пяти учителей.
Необходимо определить тесноту связи между возрастом (х) и количеством детей (у) в выделенной группе учителей.
возраст выступает как факторный признак, а количество детей этом распределении как
- как результативный.

Пример
Все коэффициенты корреляции изменяются в пределах от О
до ｱ1.
Чем ближе значение коэффициента к 0, тем меньше,
слабее связь между признаками
и чем ближе величина коэффициента к +.1, тем сильнее, значительнее, весомее связь между
признаками.
Если коэффициент корреляции принимает положительные значения - связь между признаками прямая,
т.е. с увеличением значения одного признака - растет среднее значение второго.
Если коэффициент корреляции имеет значение меньше О
(т.е. отрицательное) - связь обратная.

Пример
При r больше или равным ｱ0,5 можно констатировать наличие существенной связи между признаками.
Оценка значимости r во многом зависит от объема исследуемой совокупности.
Если число наблюдений велико, то даже небольшая величина коэффициента линейной корреляции имеет определенную значимость, которой не следует пренебрегать.
Это проверяется специальными статистическими таблицами, раскрывающими зависимость
величины г от объема изучаемой совокупности.

Пример
нашем примере - связь между признаками очень тесная и прямая,
т.е. количество детей в семье в значительной мере зависит от возраста родителей и чем старше опрашиваемый, тем
больше у него детей.

коэффициент корреляции
Линейный коэффициент корреляции может принимать значения от –1 до 1.
Чем ближе величина коэффициента корреляции к предельным значениям, тем теснее взаимосвязь между признаками.
Равенство коэффициента нулю свидетельствует об отсутствии линейной связи между признаками.

Коэффициент корреляции
Если коэффициент корреляции положительный (до 1),
то между признаками существует прямая функциональная зависимость,
если отрицательный, то обратная

Ограничения применения коэффициента линейной корреляции
Во-первых, он исчисляется только для количественных признаков.
Во-вторых, признаки, связь между которыми выявляется, должны быть нормально распределены.
В-третьих, связь, сила которой должна быть измерена, должна быть линейной.
До вычисления коэффициента следует проверить имеющиеся данные на соответствие, предъявляемым условиям.
Нормальность и линейность проверяются графчески
Приведенная формула определения величины r применяется
только для первичных, несгруппированных данных.

Другие коэффициенты корреляции
При анализе исторических событий исследователи работают
преимущественно с качественными признаками, разновидностью
которых выступают альтернативные (здесь: принимающие только два значения).
Для изучения силы их связи применяются
коэффициент ассоциации (Q) и коэффициент сопряженности
(Ф) или коэффициент контингенции (Kk).

Другие коэффициенты корреляции
Их вычисление предваряется тем, что имеющиеся данные сводятся в таблицу четырех полей:
а затем ведется расчет по формулам

Благодарю за внимание!