1. Диагональ куба равна . Найдите его объем.

2. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.

3. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60о. Одно из ребер параллелепипеда составляет с этой гранью угол в 60о и равно 2. Найдите объем параллелепипеда.

4. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

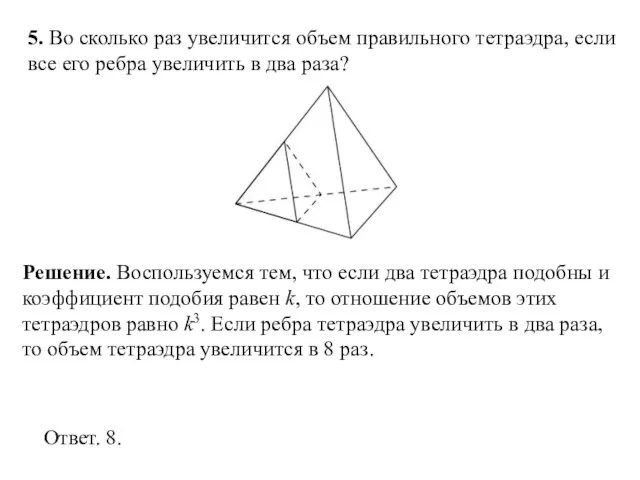
5. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?

6. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности пирамиды.

7. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.

8. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

9. В цилиндрический сосуд, в котором находится 6 дм3 воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?

10. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

11. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.