20220906___1__v3

Как зовут преподавателя?
Дударин Павел Владимирович, к.т.н. доцент каф. “Информационные системы”
Преподаватель – любитель
Исследование операций и методы оптимизации
Вычислительная математика
Дискретная математика в биоинформатике
Математические методы в научных исследования
Образование:
- Аспиртанура УлГТУ (математическое моделирование, численные методы и комплексы программ)
- Специалитет УлГУ (прикладная математика и информатика)
В обычной жизни:
ИБС - технический директор продуктового направления (7 лет)
Авиакомпания Волга-Днепр (10 лет)

Правила игры
Старосты – списки групп в гуглдоке или яндекс документах.
Два семестра, каждый по два цикла. В каждом семестре сначала лекции и семинары (решение задач в группах по 3-4 человека).
Потом лабораторные работы в классе (по 2-4 лабы в каждом семестре). Лабы будут по командам. Плюсы / минусы?
Самые активные на паре (лекции и семинары) получают 5, 8 или 10 баллов.
В первом семестре зачет. Допуск к зачету - все лабы вовремя. Зачет = репетиция экзамена на объеме семестра.
Во втором семестре экзамен. Автоматов не будет, но будут плюшки на экзамене:
Готовиться только к 2-м вопросам
Возможность отвечать на экзамене только на 1 вопрос по выбору из двух
Плюс 1 или 2 балла (можно прибавлять только к 3-ке и 4-ке)
Ваши предложения?

Вычислительная математика
Численные методы / Численный анализ
Зачем, если мы уже и так умеем решать уравнения?
Практика языка
Гимнастика
Меньше магии

Задача-разминка
1. Задача из области оптимального проектирования.
Пусть коробка изготовляется из прямоугольного листа материала размером a ×b, a < b . Для этого из четырех углов прямоугольника вырезаются квадраты со стороной x и материал сгибается вдоль линий, отмеченных на рисунке штриховыми линиями
Задача определить x при котором достигается максимальный объем получившейся коробки

Задача-разминка
1. Задача из области оптимального проектирования.
Пусть коробка изготовляется из прямоугольного листа материала размером a ×b, a < b . Для этого из четырех углов прямоугольника вырезаются квадраты со стороной x и материал сгибается вдоль линий, отмеченных на рисунке штриховыми линиями
Задача определить x при котором достигается максимальный объем получившейся коробки

Основные темы вычислительной математики
Методы оценки погрешностей̆
Численные методы решения систем и уравнений
Аппроксимация и интерполяция таблично заданных функций
Численное интегрирование
Численные методы решения дифференциальных уравнений
Модели линейного программирования и его приложения
Модели нелинейного программирования

В предыдущих сериях…

В предыдущих сериях… (Пределы)

В предыдущих сериях… (Последовательности)

В предыдущих сериях… (значения функции)

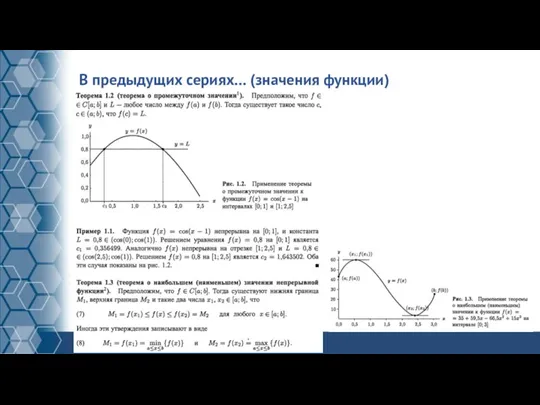
В предыдущих сериях… (Дифференцирование 1)

В предыдущих сериях… (Дифференцирование 2)

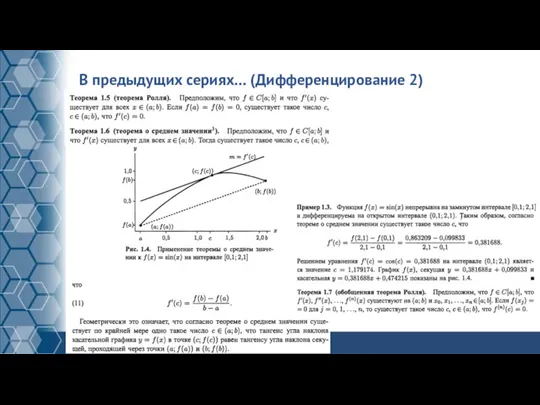
В предыдущих сериях… (Интегралы 1)

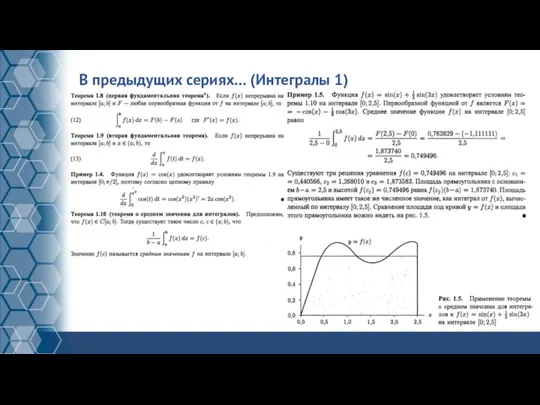
В предыдущих сериях… (Интегралы 2)

В предыдущих сериях… (Ряды)

В предыдущих сериях… (Ряд Тейлора)

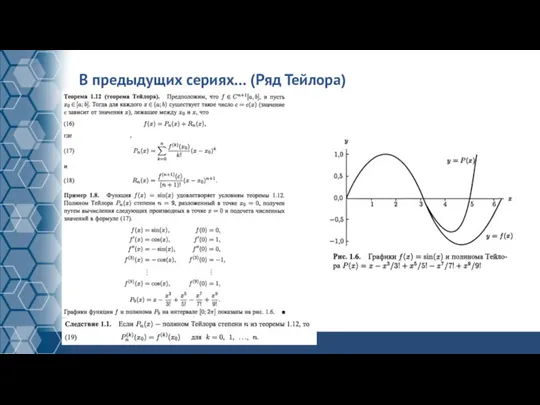
В предыдущих сериях… (вычисление полиномов)

В предыдущих сериях… (метод Горнера)

Практические задания по введению – команда 1
1.
с = 3
2.
1
3.

Практические задания по введению – команда 2
1.
-1
2.
0
3.

Практические задания по введению – команда 3
1.
с = -5
2.
0
3.

Практические задания по введению – команда 4
1.
3/2
2.
3.

Практические задания по введению – команда 5
1.
с = 10
2.
-1
3.
[-3;4]

Практические задания по введению – команда 6
1.
- 2/3
2.
-1
3.

Практические задания по введению – команда 7
1.
с = -2
2.
? / 2
3.
[-4;3]