Содержание
- 2. Confidence coefficient (confidence level) is a probability with which the inequality takes place, i.e. Remark. The
- 3. The interval which covers the unknown parameter with prescribed probability is called confidence interval (CI). —
- 4. s.2. Distributions of the RV, which are often used in statistics. Chi-squared distribution Let RV are
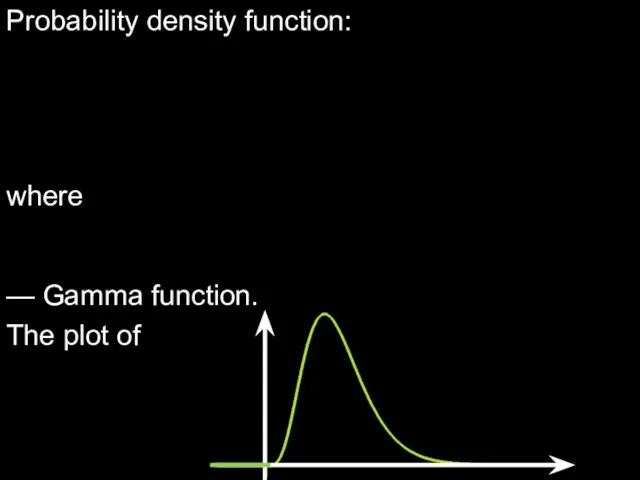
- 5. Probability density function: where — Gamma function. The plot of
- 6. The expected value: The variance: The quantile of the distribution, which corresponds the statistical significance ,
- 7. Student’s t-distribution (t-distribution) Let RV has the chi-squared distribution with k degrees of freedom. Then the
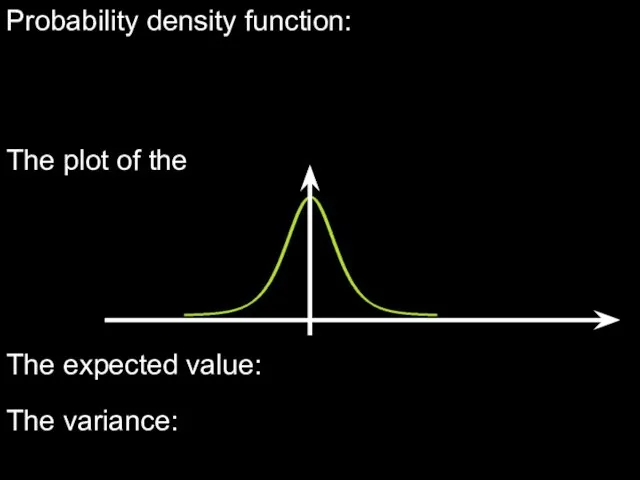
- 8. Probability density function: The plot of the The expected value: The variance:
- 9. The quantile of the t-distribution, which corresponds the statistical significance , is a such value that
- 10. s.3. Confidence Intervals for Unknown Mean and Known Standard Deviation. Let We know We should find
- 11. Let is a sample obtained from the observations for the RV X. The values change from
- 12. i.e.
- 13. Since then Let us denote Then and
- 14. Therefore i.e. with confidence level we can assert than CI covers unknown parameter a, and the
- 15. Example. Let we have sample of the RV Find 95% confidence interval for the mean. Solution.
- 16. s.4. Confidence Intervals for Unknown Mean and Unknown Standard Deviation. Let We know We should find
- 17. Let S is a standard error. Consider the following RV We can prove that T has
- 18. Let us divide the both sides of the inequality in brackets on or Let us denote
- 19. i.e. with confidence level we can assert than CI Therefore or covers unknown parameter a, and
- 20. Example. In the previous example find CI for the unknown mean, if standard deviation is unknown.
- 22. Скачать презентацию

















 بررسی HierarchyID
بررسی HierarchyID Презентация на тему: Пейзажная лирика Ф.И.Тютчева
Презентация на тему: Пейзажная лирика Ф.И.Тютчева Презентация на тему Кубизм
Презентация на тему Кубизм Проблемы массовых коммуникаций с клиентами. Пути их решения на современном этапе развития CRM
Проблемы массовых коммуникаций с клиентами. Пути их решения на современном этапе развития CRM Черное - Белое
Черное - Белое Основные виды тропов
Основные виды тропов Чувствительный элемент датчики
Чувствительный элемент датчики Их имена прославили Россию
Их имена прославили Россию ИНВЕСТИЦИОННОЕ ПРЕДЛОЖЕНИЕ«Строительство спортивно-оздоровительного центра ФК «Витебск» в деревне Берники Витебского района»
ИНВЕСТИЦИОННОЕ ПРЕДЛОЖЕНИЕ«Строительство спортивно-оздоровительного центра ФК «Витебск» в деревне Берники Витебского района» ТЕРМОДИНАМИКА И КИНЕТИКА ПРОЦЕССА ИНТЕРКАЛЯЦИИ/ДЕИНТЕРКАЛЯЦИИ В СУБМИКРОННЫХ ЧАСТИЦАХ КАТОДА ЛИТИЕВЫХ БАТАРЕЙ В сотрудничество
ТЕРМОДИНАМИКА И КИНЕТИКА ПРОЦЕССА ИНТЕРКАЛЯЦИИ/ДЕИНТЕРКАЛЯЦИИ В СУБМИКРОННЫХ ЧАСТИЦАХ КАТОДА ЛИТИЕВЫХ БАТАРЕЙ В сотрудничество  Русский язык 6 класс Презентация по теме: «Сочинение по картине»
Русский язык 6 класс Презентация по теме: «Сочинение по картине» Презентация на тему Нервная система Рефлекс Инстинкт
Презентация на тему Нервная система Рефлекс Инстинкт Религиозная толерантность
Религиозная толерантность Презентация к уроку музыки
Презентация к уроку музыки Зубная паста с углём
Зубная паста с углём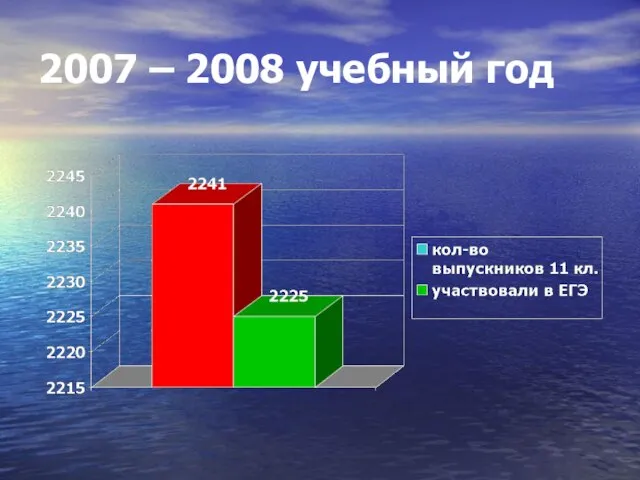 2007 – 2008 учебный год
2007 – 2008 учебный год Опочка
Опочка Устойчивость к магнитному полю промышленной частоты
Устойчивость к магнитному полю промышленной частоты Железо элемент побочной подгруппы
Железо элемент побочной подгруппы Коммерческое предложение для ООО Центр КДМ
Коммерческое предложение для ООО Центр КДМ Оплата образовательных услуг
Оплата образовательных услуг Презентация на тему Князья Киевской Руси
Презентация на тему Князья Киевской Руси Изготовление глухого и крапанового кастов
Изготовление глухого и крапанового кастов Dmitry Sergeyevich Likhachov
Dmitry Sergeyevich Likhachov Создание единого реестра застройщиков
Создание единого реестра застройщиков Право социального обеспечения
Право социального обеспечения Концепция развития: Общественно-деловой квартал Зингер
Концепция развития: Общественно-деловой квартал Зингер Алгоритмы ветвления.Оператор выбора
Алгоритмы ветвления.Оператор выбора