Понятие системы трилинейных координат.
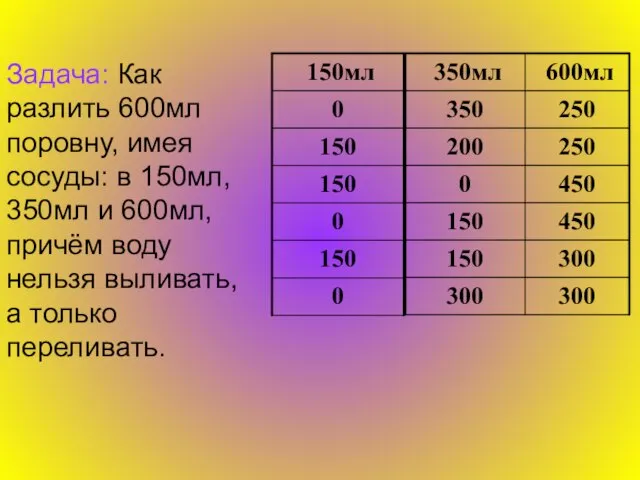
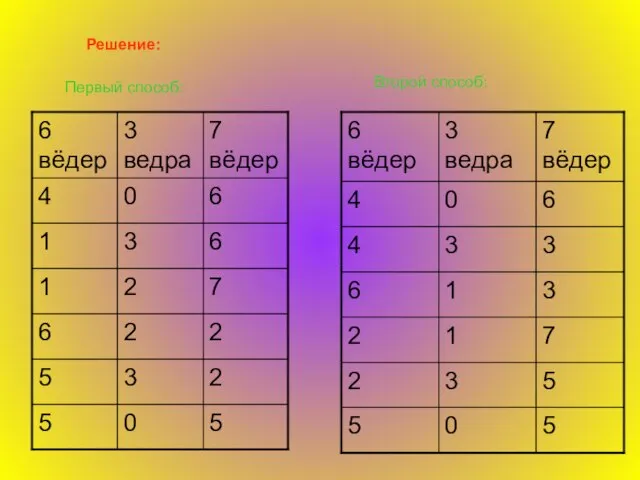
Рассмотрим применение геометрии к решению задач, в которых требуется разделить жидкость на определенные пропорции с помощью инструментов, казалось бы, непригодных для этого. Для решения нам понадобятся так называемые трилинейные координаты, которые мы сейчас и опишем.
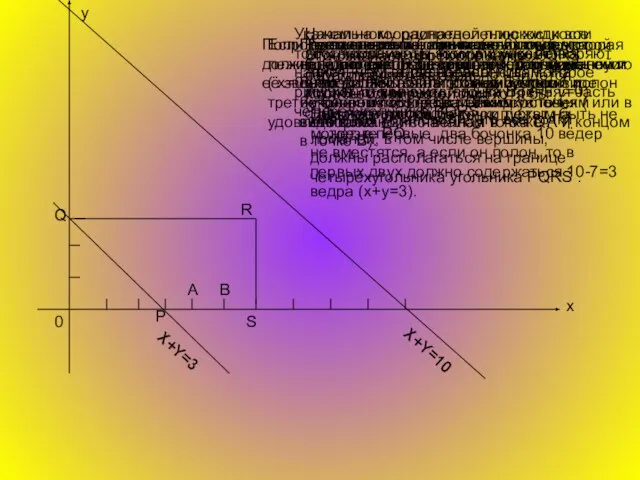
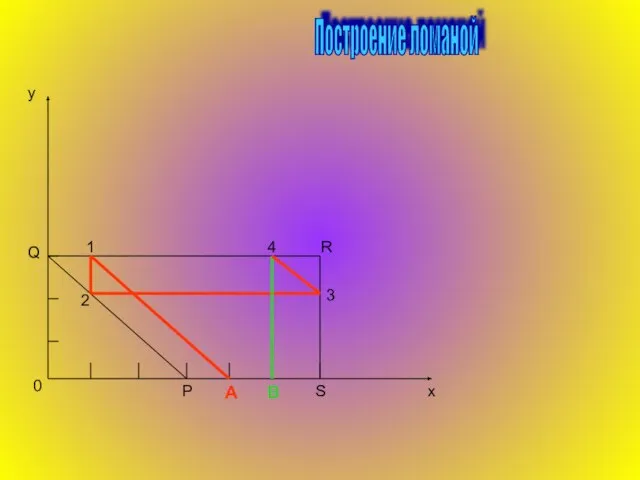
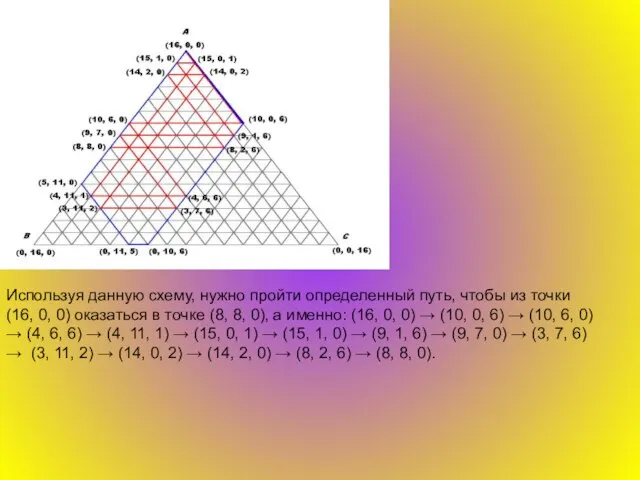
Обычно для нанесения точек с заданными декартовыми координатами пользуются миллиметровой бумагой. Для наших целей лучше использовать триангулированную бумагу, т. е. бумагу, на которой проведены три системы параллельных линий, разбивающих ее на маленькие равносторонние треугольники. Нарисуем на такой бумаге большой равносторонний треугольник АВС со сторонами, проходящими по линиям сетки. Для произвольной точки Р в этой плоскости определим числа x, y, z как расстояния от этой точки до прямых ВС, СА и АВ соответственно, причем для каждой из этих прямых расстояние будем считать положительным, если точка лежит по ту же сторону от этой прямой, что и треугольник АВС, и отрицательным в противном случае. Полученную тройку чисел (x, y, z) будем называть трилинейными координатами точки Р относительно треугольника АВС. Заметим, что для точек, лежащих внутри треугольника АВС, все три координаты положительны. Кроме того, если а – длина стороны треугольника, а h – высоты(
), то
(ax+ay+az) = SPBC + SPCA + +SPAB = SABC =
ah, откуда следует, что x + y + z = h.
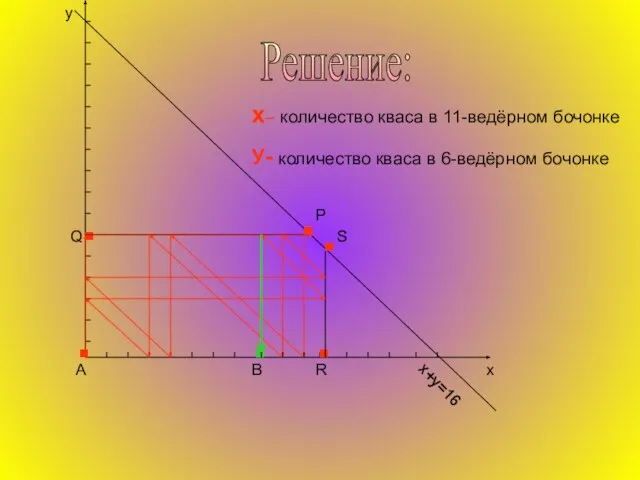
Трилинейные координаты чрезвычайно удобны для описания ситуации, в которой участвуют три переменные величины, имеющие постоянную сумму. Если одна из этих величин x, y или z остается постоянной, а две другие изменяются, то точка (x, y, z) движется по прямой, параллельной одной из сторон треугольника АВС. В частности, прямые, на которых лежат стороны ВС, СА и АВ, описываются уравнениями: x = 0, y = 0, z = 0, а вершины А, В, С имеют координаты (h, 0, 0), (0,h,0), (0, 0, h).







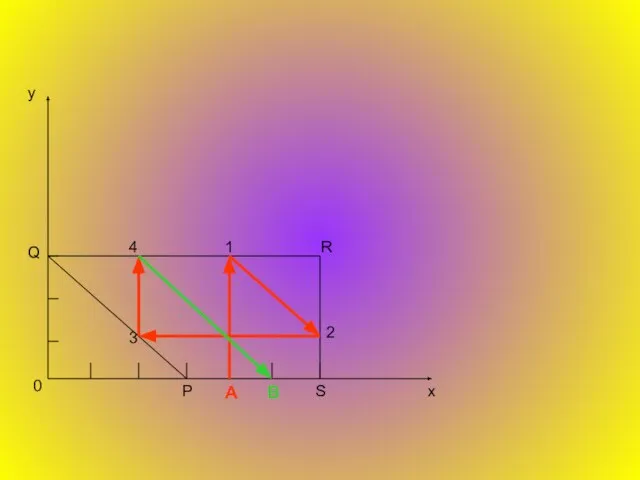











 Совершенствование системы мотивирования на предприятии
Совершенствование системы мотивирования на предприятии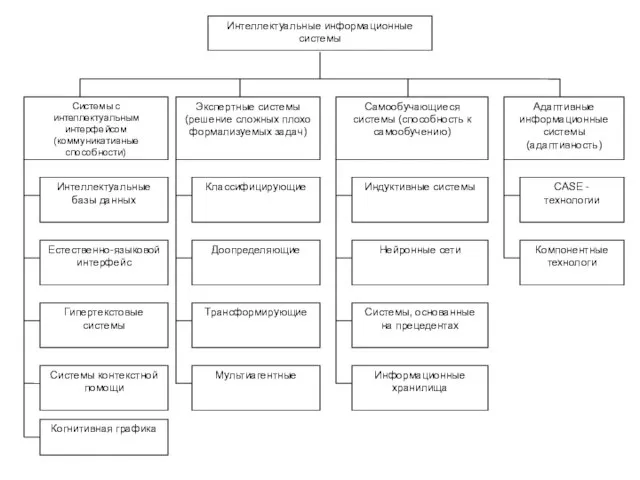 Интеллектуальные информационные системы
Интеллектуальные информационные системы Торговые обычаи
Торговые обычаи Турпредприятие моей мечты
Турпредприятие моей мечты Презентация на тему Размножение покрытосеменных
Презентация на тему Размножение покрытосеменных Оплата банковской картой
Оплата банковской картой Гарантии независимости судей
Гарантии независимости судей Аксонометрические проекции предметов имеющих круглые поверхности
Аксонометрические проекции предметов имеющих круглые поверхности Виды лингвистических тренажеров
Виды лингвистических тренажеров Стендаль (Мари Анри Бейль)
Стендаль (Мари Анри Бейль) МОЯ Семья
МОЯ Семья ПЕДАГОГИЧЕСКИЙ ПОРТФОЛИО
ПЕДАГОГИЧЕСКИЙ ПОРТФОЛИО Управление запасами в логистике. Выбор варианта поставок
Управление запасами в логистике. Выбор варианта поставок Город деловых людей
Город деловых людей Анализ ситуации в отрасли. Действия розничного торговца в зависимости от жизненного цикла розничной организации
Анализ ситуации в отрасли. Действия розничного торговца в зависимости от жизненного цикла розничной организации ЧЕЛОВЕК И МИР ЛЮДЕЙ
ЧЕЛОВЕК И МИР ЛЮДЕЙ Семейный бюджет. Расходы
Семейный бюджет. Расходы Системно-деятельностный подход
Системно-деятельностный подход Происхождение жизни на земле
Происхождение жизни на земле Гражданская война в 1919-1920 гг.
Гражданская война в 1919-1920 гг. Компания Репаблик Групп
Компания Репаблик Групп Examples of irregular verbs
Examples of irregular verbs Правовой режим вод (тема 4)
Правовой режим вод (тема 4) Презентация на тему Художественная культура Античности
Презентация на тему Художественная культура Античности Proyecto en Lengua Española
Proyecto en Lengua Española Презентация на тему Строение и функции почек 8 класс
Презентация на тему Строение и функции почек 8 класс Презентация на тему Проверка выдвинутых версий
Презентация на тему Проверка выдвинутых версий  ДНЕВНАЯ СПОРТИВНАЯ ПРОГРАММА
ДНЕВНАЯ СПОРТИВНАЯ ПРОГРАММА