Лилия Николенко. Ташкент. Узбекистан

Лилия Николенко. Ташкент. Узбекистан
История открытия теоремы
Так, оптимист Михайло Ломоносов (1711 -1765) писал: "Пифагор за изобретение одного геометрического правила Зевесу принес на жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось".
А вот ироничный Генрих Гейне (1797-1856) видел развитие той же ситуации несколько иначе: "Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принес в жертву бессмертным богам".
И хотя сегодня теорема Пифагора обнаружена в различных частных задачах и чертежах: и в египетском треугольнике в папирусе времен фараона Аменемхета I (ок. 2000 до н.э.), и в вавилонских клинописных табличках эпохи царя Хаммурапи (XVIII в. до н.э.), и в древнейшем китайском трактате "Чжоу-би суань цзинь" ("Математический трактат о гномоне"), время создания которого точно не известно, но где утверждается, что в XII в. до н.э. китайцы знали свойства египетского треугольника, а к VI в. до н.э. - и общий вид теоремы, и в древнеиндийском геометрическо-теологическом трактате VII - V вв. до н.э. "Сульва сутра" ("Правила веревки"),- несмотря на все это, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадется. То же относится и к легенде о заклании быков Пифагором. Да и вряд ли нужно препарировать историко-математическим скальпелем красивые древние предания.
Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги "Начал" Евклида, пишет: "Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принес в жертву быка". Впрочем, более щедрые сказители одного быка превратили в одну гекатомбу, а это уже целая сотня. И хотя еще Цицерон заметил, что всякое пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие отклики.
Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов. Поэтому нам ничего не остается, как рассмотреть некоторые классические доказательства теоремы Пифагора, известные из древних трактатов. Сделать это полезно еще и потому, что в современных школьных учебниках дается алгебраическое доказательство теоремы. При этом бесследно исчезает первозданная геометрическая аура теоремы, теряется та нить Ариадны, которая вела древних мудрецов к истине, а путь этот почти всегда оказывался кратчайшим и всегда красивым.

Лилия Николенко. Ташкент. Узбекистан
Как сформулировал теорему Пифагор?
Теорема Пифагора. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
Как сформулирована теорема Пифагора в современных учебниках ?
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Лилия Николенко. Ташкент. Узбекистан
Классическое доказательство теоремы Пифагора:
Доказательство.
Рассмотрим прямоугольный треугольник с катетами а, b и гипотенузой с (рис 1). Докажем, что с2 = а2 + b2.
Достроим треугольник до квадрата со стороной (а+b) так, как показано на рисунке 2. Площадь S этого квадрата равна (a+b)2. С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из них равна
(1/2 а * b ), и квадрата со стороной с, поэтому площадь квадрата
S = 4 * 1/2ab + c2 = 2ab + c2.
Таким образом,
(а + b)2 = 2аb + с2
a2 + 2ab +b2 = 2ab + c2
откуда
с2 = а2 + b2.
ч.т.д.
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Лилия Николенко. Ташкент. Узбекистан
Древнекитайское доказательство теоремы Пифагора
Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла "Математика в девяти книгах" - главное из сохранившихся математико-астрономических сочинений.
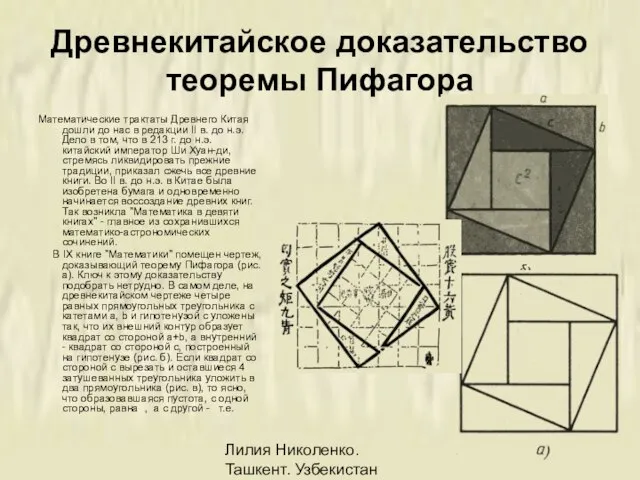
В IX книге "Математики" помещен чертеж, доказывающий теорему Пифагора (рис. а). Ключ к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний - квадрат со стороной с, построенный на гипотенузе (рис. б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. в), то ясно, что образовавшаяся пустота, с одной стороны, равна , а с другой - т.е.

Лилия Николенко. Ташкент. Узбекистан
Доказательство ан-Найризий
Багдадский математик и астроном X в. ан-Найризий (латинизированное имя - Аннариций) в арабском комментарии к "Началам" Евклида дал следующее доказательство теоремы Пифагора (рис.). Квадрат на гипотенузе разбит у Аннариция на 5 частей, из которых составляются квадраты на катетах. Конечно, равенство всех соответствующих частей требует доказательства, но мы его за очевидностью оставляем читателю. Любопытно, что доказательство Аннариция является простейшим среди огромного числа доказательств теоремы Пифагора методом разбиения: в нем фигурирует всего 5 частей (или 7 треугольников). Это наименьшее число возможных разбиений.

Лилия Николенко. Ташкент. Узбекистан
Наглядное доказательство теоремы Пифагора
32424