Содержание
- 2. Символічний метод аналізу гармонічних режимів Символічний метод ґрунтується на переході від опису гармонічних сигналів косинусними або
- 3. Описи узагальненого двополюсника
- 4. Відповідно до символічного методу аналіз гармонічного режиму лінійного електричного кола зводиться до дослідження його лінійного резистивного
- 5. Будь-яке лінійне пасивне двополюсне електричне коло, гілку або окремий двополюсник у частотній області при зображенні гармонічних
- 6. Основні етапи аналізу гармонічного режиму символічним методом Будують комплексну схему заміщення заданого для аналізу кола заміною
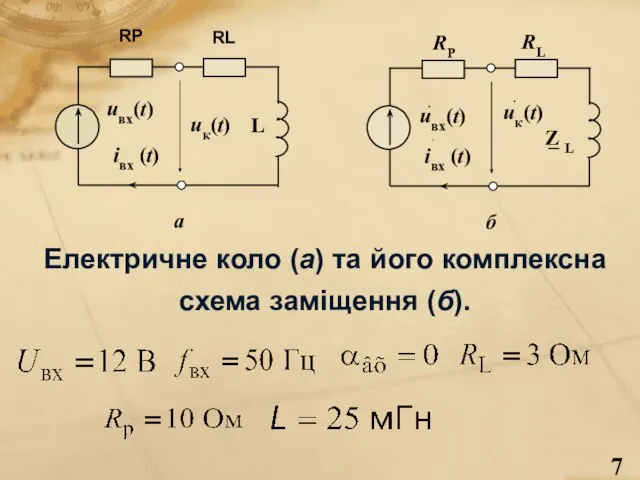
- 7. Електричне коло (а) та його комплексна схема заміщення (б).
- 9. Закони Кірхгофа у символічній формі При переході до символічних зображень їх частотні еквіваленти мають стільки ж
- 11. До вузла електричного кола підключені три гілки (див. рис.). Струм першої , другої , а третьої
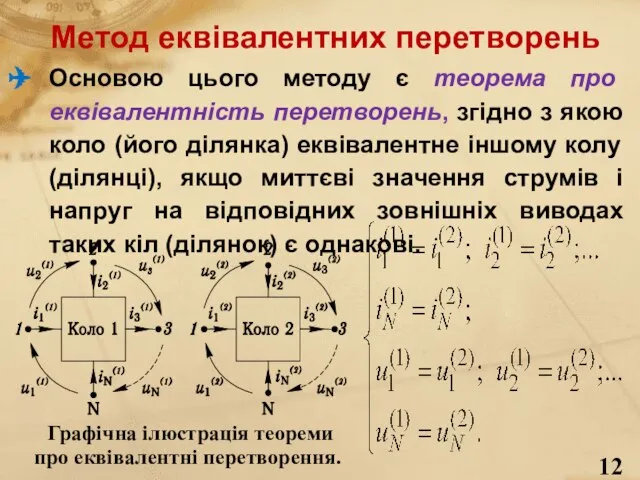
- 12. Основою цього методу є теорема про еквівалентність перетворень, згідно з якою коло (його ділянка) еквівалентне іншому
- 13. Первинні та вторинні параметри електричних кіл Шукані струм та напругу (реакції) електричних кіл називають первинними параметрами,
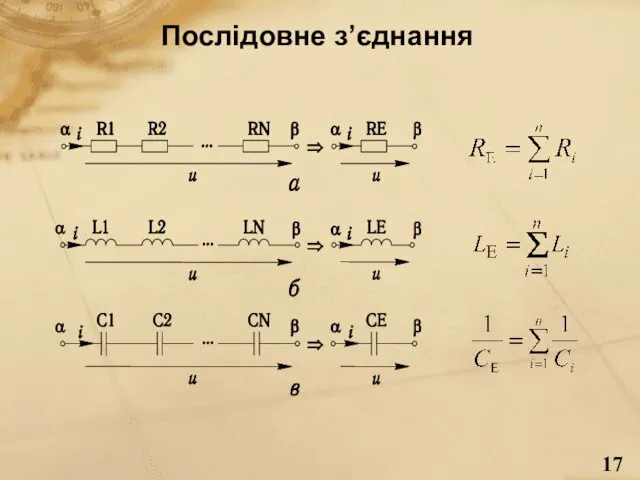
- 16. Найхарактерніші види еквівалентних перетворень послідовного та паралельного з’єднань; з’єднання зірки на трикутник та навпаки; джерел; на
- 17. Послідовне з’єднання
- 18. Подільник напруги Двоелементні подільники напруги
- 20. Основні властивості подільника напруги загальна (вхідна) напруга ділиться між елементами пропорційно опору; коефіцієнт пропорційності між напругою
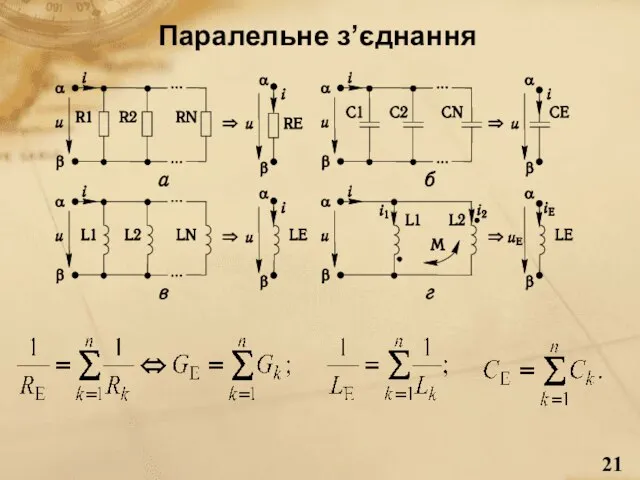
- 21. Паралельне з’єднання
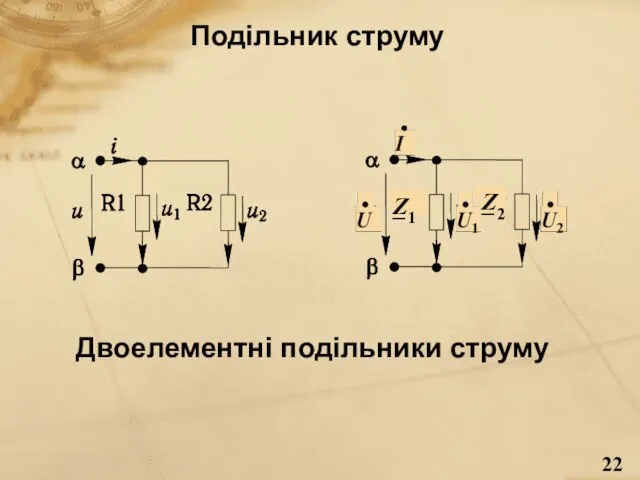
- 22. Подільник струму Двоелементні подільники струму
- 24. Основні властивості подільника струму загальний (вхідний) струм ділиться між елементами пропорційно провідності або обернено пропорційно опору;
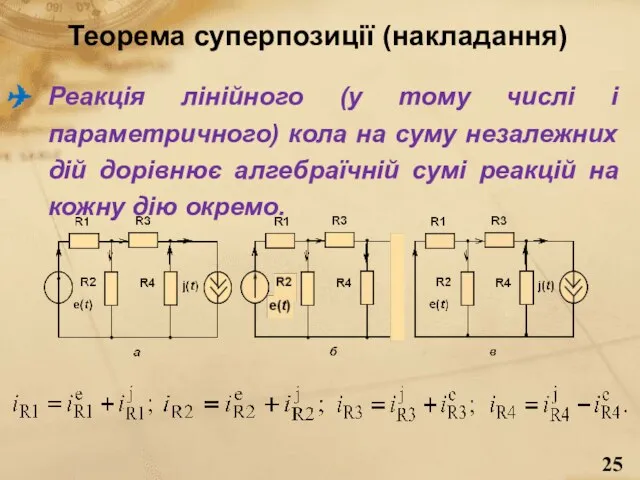
- 25. Теорема суперпозиції (накладання) Реакція лінійного (у тому числі і параметричного) кола на суму незалежних дій дорівнює
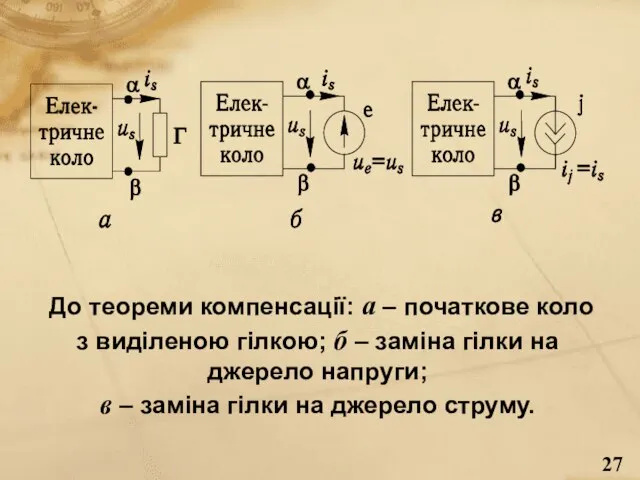
- 26. Теорема компенсації або заміщення Будь-яку (не обов’язково лінійну) кондуктивно зв’язану з іншими частинами кола гілку з
- 27. До теореми компенсації: а – початкове коло з виділеною гілкою; б – заміна гілки на джерело
- 28. Теорема про еквівалентний генератор або активний двополюсник Будь-яке лінійне активне електричне коло відносно його деякого двополюсного
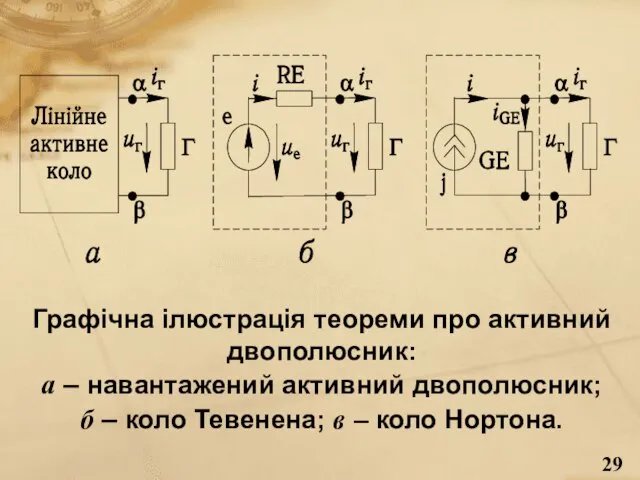
- 29. Графічна ілюстрація теореми про активний двополюсник: а – навантажений активний двополюсник; б – коло Тевенена; в
- 30. Основні співвідношення до теореми про еквівалентний генератор
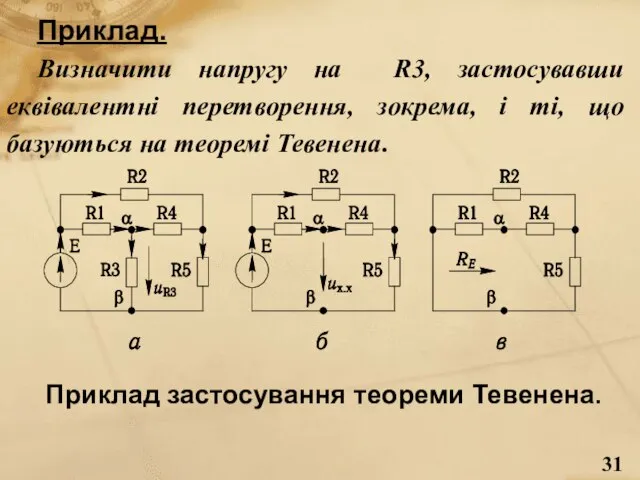
- 31. Приклад. Визначити напругу на R3, застосувавши еквівалентні перетворення, зокрема, і ті, що базуються на теоремі Тевенена.
- 33. Д Я К У Ю З А У В А Г У !
- 35. Скачать презентацию






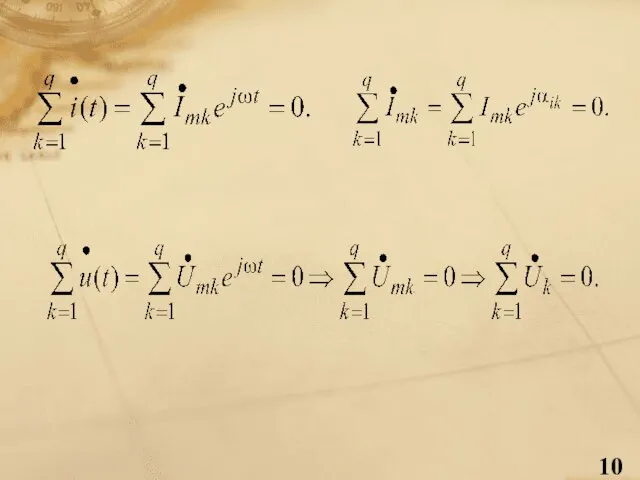


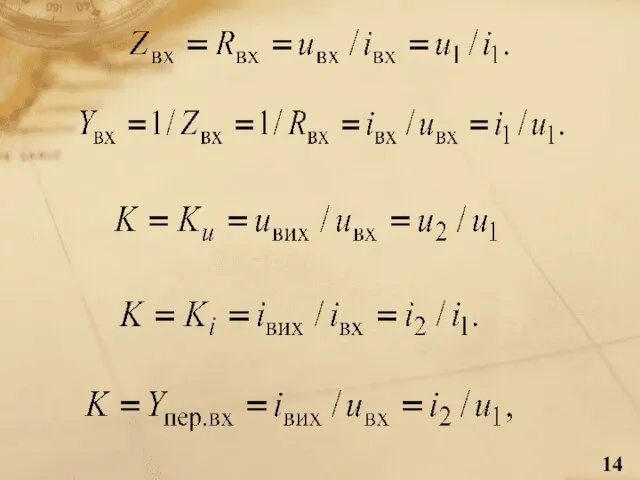
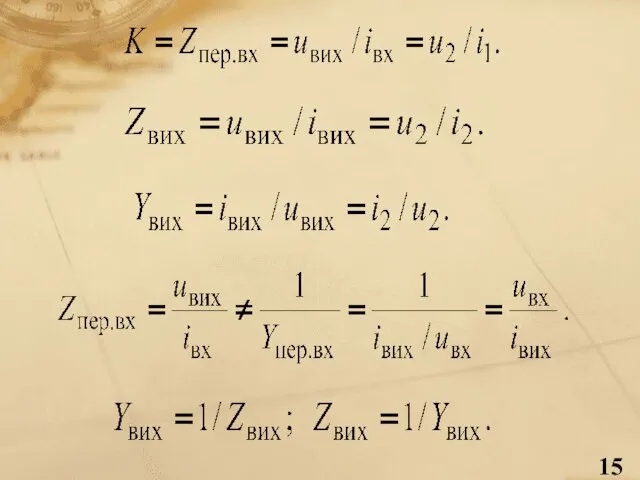


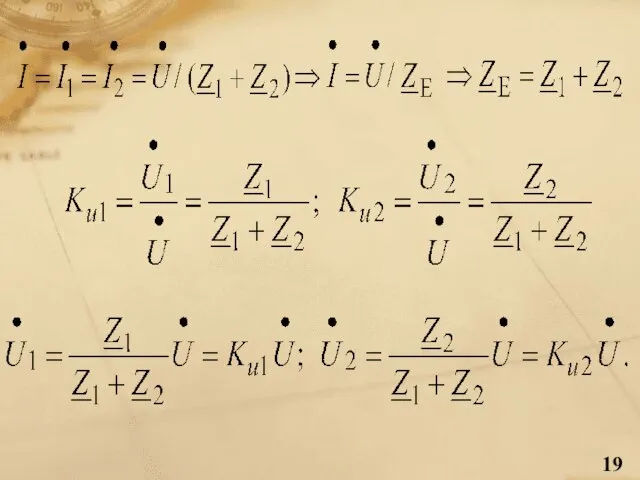

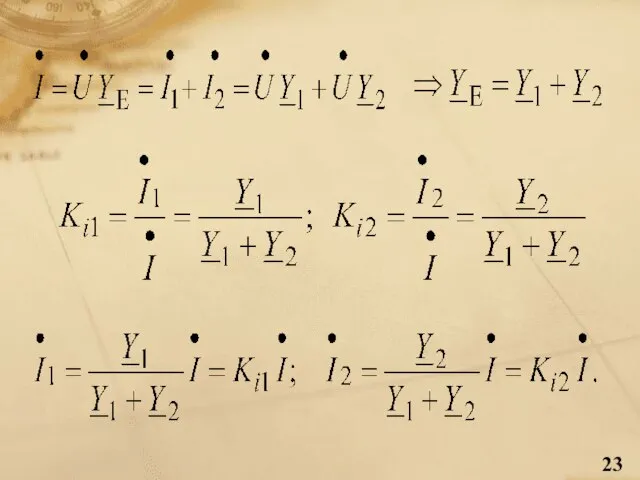




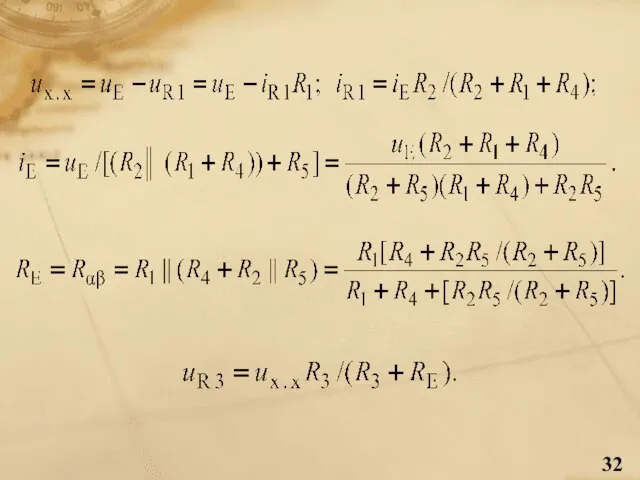

 Инструкция по получению учебно-методических материалов в личном кабинете студента
Инструкция по получению учебно-методических материалов в личном кабинете студента Презентация на тему Внутренняя политика Ивана Грозного. Последние годы правления.
Презентация на тему Внутренняя политика Ивана Грозного. Последние годы правления.  Мануал по решению основных проблем при переводе с японского на русский
Мануал по решению основных проблем при переводе с японского на русский Путешествие по Смольному монастырю
Путешествие по Смольному монастырю Презентация на тему Собор святой Софии в Константинополе
Презентация на тему Собор святой Софии в Константинополе Дизайн-менеджмент
Дизайн-менеджмент Семинар SLS в Новосибирске. - презентация
Семинар SLS в Новосибирске. - презентация Организация работы классного руководителя
Организация работы классного руководителя Загадки о цветах
Загадки о цветах Как работать с заданиями. Пошаговая инструкция для студентов ФНиДО БГУИР
Как работать с заданиями. Пошаговая инструкция для студентов ФНиДО БГУИР Мы и дорога
Мы и дорога Использование компьютерных технологий в начальной школе
Использование компьютерных технологий в начальной школе www.brianna-trans.com
www.brianna-trans.com Реклама Альфа-Банку
Реклама Альфа-Банку Пищевые продукты, питательные вещества и их превращения в организме
Пищевые продукты, питательные вещества и их превращения в организме Коэффициент графика функции
Коэффициент графика функции Приветствуем участников окружного семинара руководителей ОУ «Формирование единого информационного пространства школы».
Приветствуем участников окружного семинара руководителей ОУ «Формирование единого информационного пространства школы». Паровозик. Рисунок
Паровозик. Рисунок Аналитическо-проектная работа по анализу кадровой политики организации
Аналитическо-проектная работа по анализу кадровой политики организации ЭКОЛОГИЧЕСКОЕ ПРАВО
ЭКОЛОГИЧЕСКОЕ ПРАВО Теорема Пифагора
Теорема Пифагора ОТЧЕТ О РАБОТЕПО ЗАМЕЧАНИЯМ НА ПРОЕКТ«МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПЛАНИРОВАНИЮ И ОРГАНИЗАЦИИ ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ ПР
ОТЧЕТ О РАБОТЕПО ЗАМЕЧАНИЯМ НА ПРОЕКТ«МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПЛАНИРОВАНИЮ И ОРГАНИЗАЦИИ ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ ПР Определитель и действие с ними
Определитель и действие с ними Понятие «контроллинг»
Понятие «контроллинг» Художественная культура Древнего Египта
Художественная культура Древнего Египта Работа школы в режиме Полного Дня
Работа школы в режиме Полного Дня Новгородская земля
Новгородская земля Утверждение тоталитаризма
Утверждение тоталитаризма