Моделирование финансового риска. Оптимальный портфель ценных бумаг

Основные понятия
Финансовый рынок – рынок, на котором товарами служат деньги, банковские кредиты и ценные бумаги (облигации, акции, фьючерсы, опционы)

Эффективность финансовых операций
Предоставление в долг некоторой суммы S(0) с условием, что через время Т будет возвращена сумма S(T). Кредитор получит прибыль S(T)-S(0).
В расчете на единицу кредита
rT – эффективность операции (с точки зрения кредитора), процентная ставка, интерес
dT – дисконт – отношение прибыли к возвращаемой сумме

Эффективная ставка
Эффективной ставкой называется годичная ставка сложных процентов, которая обеспечивает заданное соотношение между возвращаемой суммой S(T) и суммой кредита S(0):
т.е.

Финансовый риск

Оптимизация портфеля ценных бумаг

Оптимизация портфеля ценных бумаг
Если mp – выбранное инвестором значение эффективности портфеля, то задача оптимизации имеет вид:

Решение задачи оптимизации
Метод множителей Лагранжа:
Из системы n+2 уравнений
находим структуру оптимального портфеля

Замечание к процессу поиска структуры оптимального портфеля

Случай некоррелированности случайных величин
Если эффективности некоррелированны, то
Оптимальная структура портфеля имеет вид
Дисперсия оптимального портфеля равна

Пример. Оптимизация портфеля ценных бумаг
Инвестор может составить портфель из трех ценных бумаг, эффективности которых R1, R2, R3 являются некоррелированными случайными величинами с числовыми характеристиками
(все данные в процентах к цене покупки).
Определить оптимальный портфель бумаг при mp = 10.

Решение
Эффективность портфеля Rp = Σ Riθi имеет математическое ожидание
и дисперсию
Получаем задачу квадратичного программирования

Решение
Составляем функцию Лагранжа
Необходимые условия экстремума

Решение
Решаем первые три уравнения системы:
Подставляем в последние два уравнения:
Находим
Получаем структуру оптимального портфеля
Дисперсия равна

Модификация портфеля ценных бумаг
Пусть инвестор может наряду с покупкой ценных бумаг делать вложения, не связанные с риском.
Необходимо определить оптимальную комбинацию рискового и безрискового части портфеля, чтобы минимизировать дисперсию при выбранной им средней эффективности портфеля mp.

Модификация портфеля ценных бумаг
Постановка задачи оптимизации
где r0 и θ0 - эффективность и доля безрисковой части портфеля соответственно.
При этом r0 < mn

Решение модифицированной задачи
Строим функцию Лагранжа
Приравниваем нулю ее производные по θi:
Решая полученную систему уравнений с учетом условий ограничений, получаем структуру оптимального портфеля

Замечание к решению

Случай некоррелируемости эффективностей
Если эффективности некоррелируемы, то

Случай некоррелируемости эффективностей
Элементы структуры оптимального портфеля имеют вид
Дисперсия портфеля
Безрисковая часть будет входить в портфель, если
Если , то в портфеле будет присутствовать только рисковая часть.
Если , то в портфеле будет присутствовать только безрисковая часть

Премия за риск
Превышение средней эффективности ценной бумаги над эффективностью безрискового вклада называется премией за риск
Премия за риск конкретной ценной бумаги, включенной в оптимальный портфель, пропорциональна премии за риск всего портфеля в целом
Коэффициент – бета-вклад j-ой ценной бумаги в
оптимальный портфель, т.е. отношение ковариации эффективности ценной бумаги и портфеля к вариации портфеля

Пример
Определить, с каким наименьшим риском можно достичь 20%-ной эффективности инвестиций, если есть возможность банковских вложений и заимствований по ставке i = 10% годовых, а на рынке ценных бумаг обращаются две акции, их ожидаемые эффективности равны соответственно r1 = 16% и r2 = 23%, риски σ1 = 5%, σ2 = 14%, а коэффициент корреляции доходностей данных акций равен ρ12 = 0,36.

Решение с помощью Excel
Вводим данные в рабочий лист. Для вычисления дисперсии портфеля учтем, что σ12 = ρ12σ1σ2

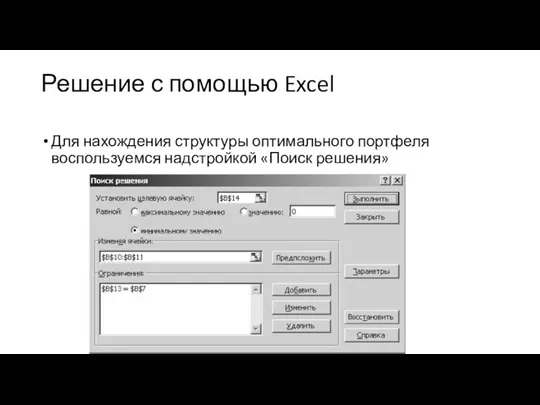
Решение с помощью Excel
Для нахождения структуры оптимального портфеля воспользуемся надстройкой «Поиск решения»

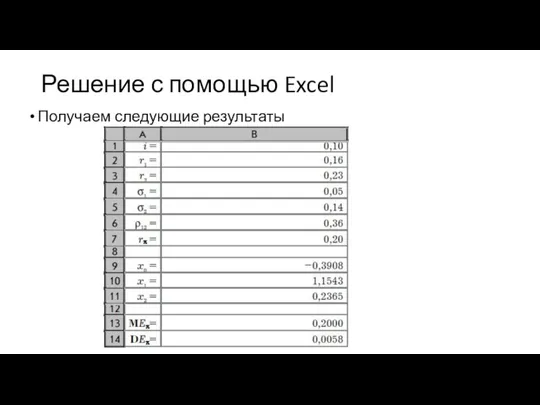
Решение с помощью Excel
Получаем следующие результаты