МОУ «ООШ с.Никольское Духовницкого района Саратовской области» Теорема Пифагора

Теорема Пифагора
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далёкий век.

« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»
« Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Формулировка
теоремы
Во времена Пифагора теорема звучала так:
или

« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
Современная формулировка

Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
Доказательства теоремы

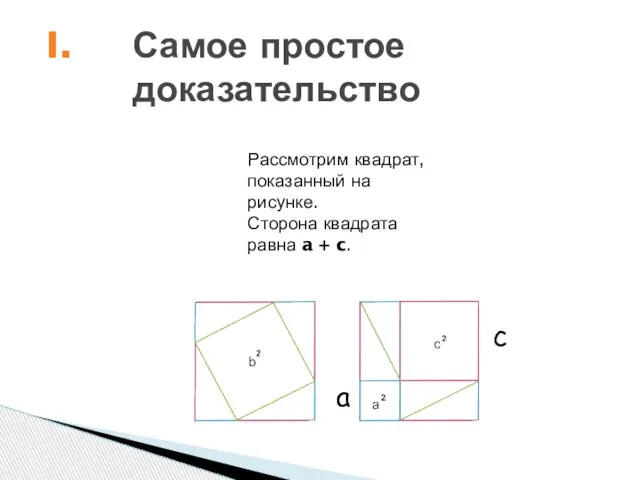
Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a + c.
c
a

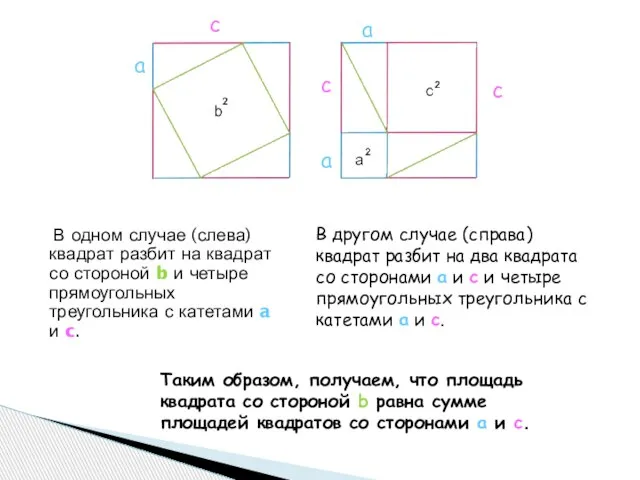
В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c.
a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.

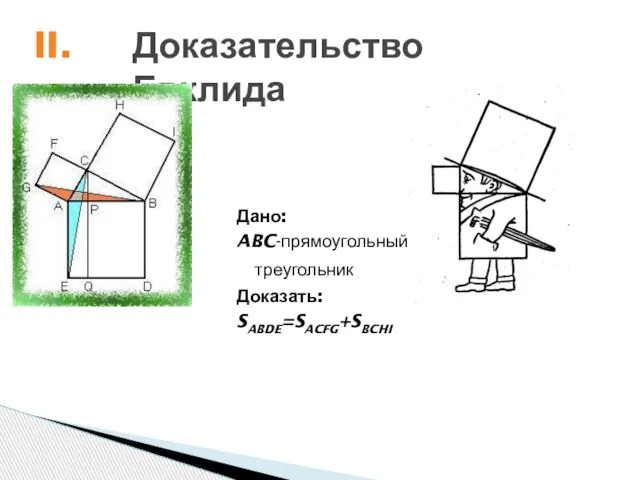
Доказательство Евклида
Дано:
ABC-прямоугольный треугольник
Доказать:
SABDE=SACFG+SBCHI

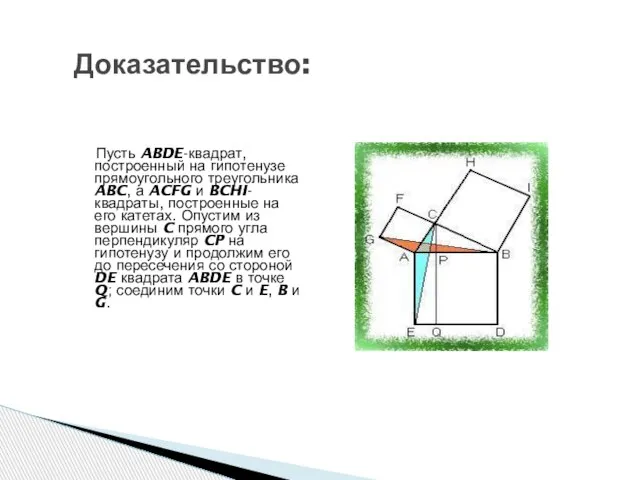
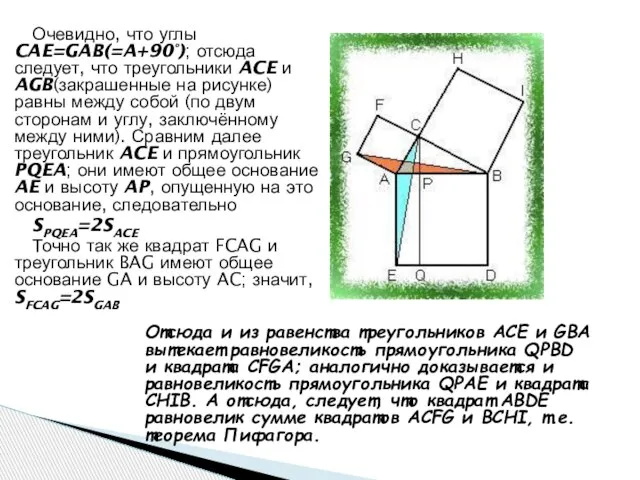
Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG и BCHI-квадраты, построенные на его катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G.

Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательно
SPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.

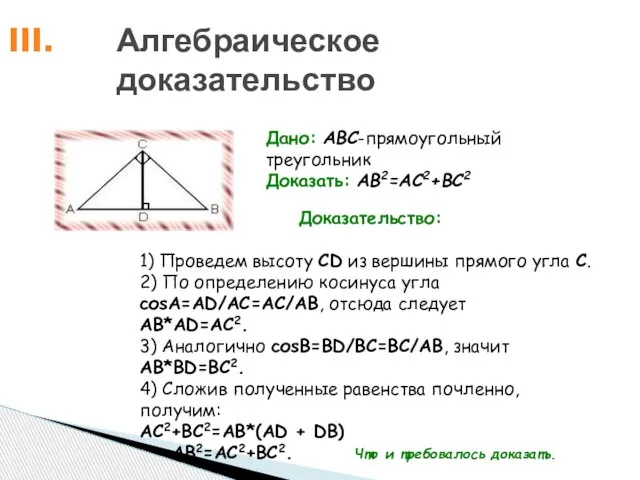
Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого угла С.
2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда следует
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.

Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E.
2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:
SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.

Теорема Пифагора- это одна из самых важных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии.
Значение теоремы Пифагора

Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum - ослиный мост, или elefuga - бегство «убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также «ветряной мельницей», составляли стихи, «Пифагоровы штаны на все стороны равны», рисовали карикатуры.