Определенный интеграл

Задача о вычислении площади плоской фигуры
Решим задачу о вычислении площади фигуры, ограниченной графиком функции , отрезками прямых
, и осью Ox.Такую фигуру называют криволинейной трапецией
a
b

Задача о вычислении площади плоской фигуры

Задача о вычислении площади плоской фигуры

Определенный интеграл

Определенный интеграл

Определенный интеграл

Теорема о существовании определенного интеграла

Свойства определенного интеграла

Свойства определенного интеграла

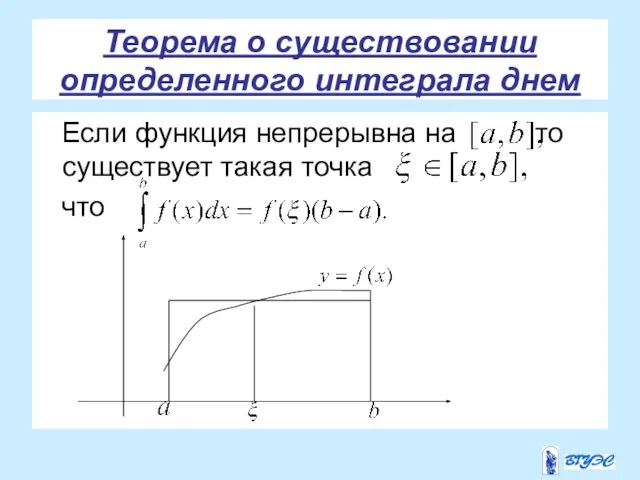
Теорема о существовании определенного интеграла днем
Если функция непрерывна на то существует такая точка
что

Вычисление определенного интеграла

Пример
Вычислить .

Вычисление интеграла

Пример

Пример

Несобственный интеграл

Пример
. Вычислить несобственный интеграл
(или установить его расходимость)
.
Этот несобственный интеграл расходится.

Пример
Несобственный интеграл

Геометрические приложения определенного интеграла

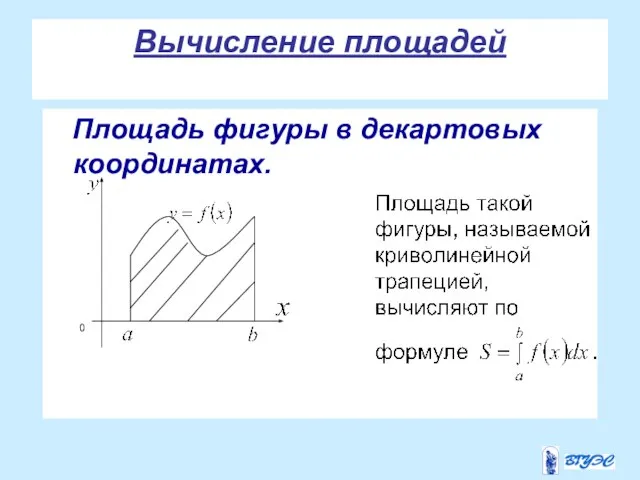
Вычисление площадей
Площадь фигуры в декартовых координатах.

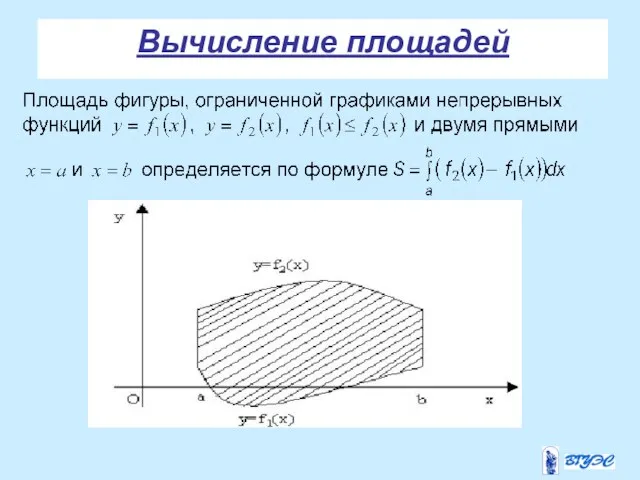
Вычисление площадей

Вычисление площадей
В случае параметрического задания
кривой, площадь фигуры, ограниченной
прямыми , осью Ох и кривой
вычисляют по
формуле
где пределы интегрирования определяют из
уравнений .
.

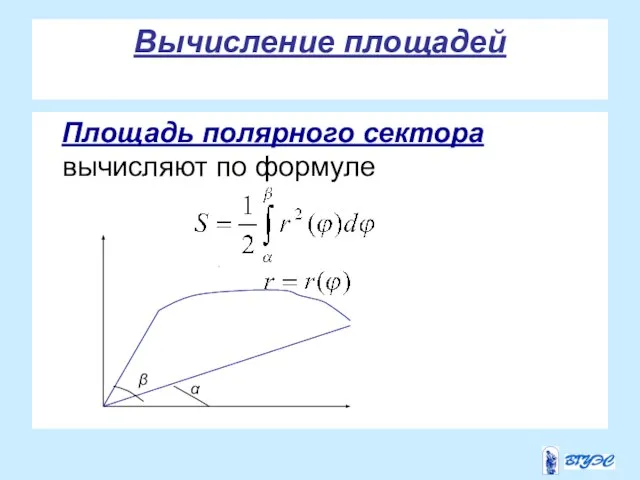
Вычисление площадей
Площадь полярного сектора вычисляют по формуле
.
α
β

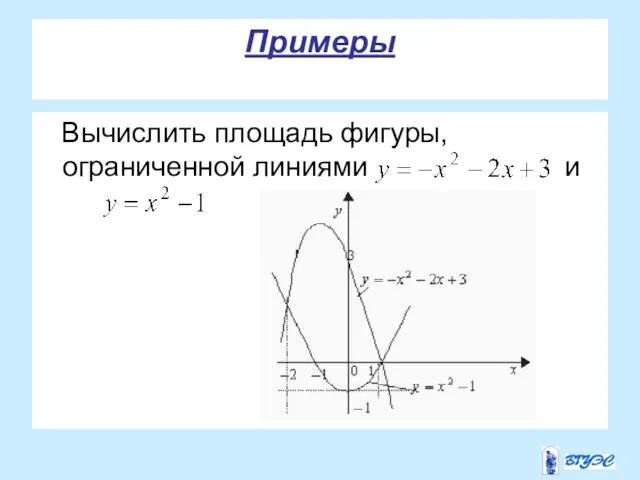
Примеры
Вычислить площадь фигуры, ограниченной линиями и

Продолжение
Получим

Примеры
Найти площадь эллипса . Параметрические уравнения эллипса
у
о
х

Пример
Площадь фигуры, ограниченной лемнискатой Бернулли
и лежащей вне круга радиуса :

Вычисление длины дуги
Если кривая задана параметрическими уравнениями , , то длина ее дуги
,
где –значения параметра, соответствующие концам дуги .

Длина дуги в декартовых координатах
Если кривая задана уравнением ,
то , где a, b–абсциссы начала и конца дуги .
Если кривая задана уравнением
, то , где c, d–ординаты начала и конца дуги

Длина дуги в полярных координатах
Если кривая задана уравнением в полярных координатах , то
,
где –значения полярного угла, соответствующие концам дуги .

Примеры
Вычислить длину дуги кривой
от точки до .
, тогда

Вычисление объема тела вращения.
Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой , отрезком оси абсцисс и прямыми , вычисляется по формуле .

Вычисление объема тела вращения
Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком оси ординат и прямыми , вычисляется по формуле
.

Вычисление объема тела вращения
Искомый объем можно найти как разность объемов, полученных вращением вокруг оси Ox криволинейных трапеций, ограниченных линиями и