Содержание
- 2. Технические характеристики очереди у среднее время, которое клиент проводит в очереди средняя длина очереди среднее время,
- 3. Пример расчета а На строительном складе работают четыре кладовщика. Поток посетителей имеет пуассоновское распределение с интенсивностью
- 4. Пример расчета Отсюда следует, что вероятность того, что все четыре кладовщика простаивают, равна 0,05. Определим другие
- 5. Пример расчета а
- 6. Пример 2 а ЗАДАНИЕ. Система массового обслуживания — билетная касса с одним окошком и неограниченной очередью.
- 7. Пример 2 РЕШЕНИЕ. Имеем систему массового обслуживания с одним каналом (однакасса) и неограниченной очередью. Интенсивность потока
- 8. Пример 2 Вычислим финальные вероятности: Вероятность простоя системы: Вероятность того, что в системе одна заявка (один
- 9. Пример 2 Вероятность того, что в системе две заявки (один пассажир у кассы и один пассажир
- 10. Пример 2 Среднее число заявок, находящихся в очереди (пассажиров в очереди) равно: Среднее время ожидания в
- 11. Пример 2 Среднее число пассажиров, покупающих билеты, равно: Среднее время обслуживания равно: Тогда среднее число заявок
- 13. Скачать презентацию










 Учет капитальных вложений. Нормативные документы Долгосрочные
Учет капитальных вложений. Нормативные документы Долгосрочные Муром
Муром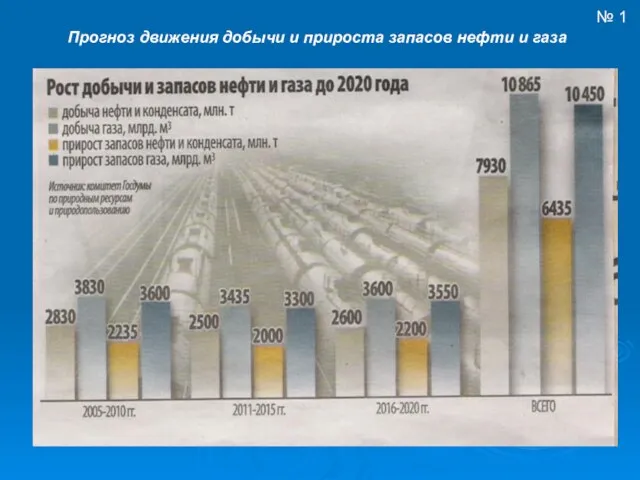 Прогноз движения добычи и прироста запасов нефти и газа
Прогноз движения добычи и прироста запасов нефти и газа Применение производной к исследованию функции.
Применение производной к исследованию функции. Лaтвия на пути к переходу на единую валюту
Лaтвия на пути к переходу на единую валюту Муниципальное общеобразовательное учреждение «Школа № 33» г.о.Саранск Комплексно – целевая программа «Здоровье»
Муниципальное общеобразовательное учреждение «Школа № 33» г.о.Саранск Комплексно – целевая программа «Здоровье» Бунт четырнадцати
Бунт четырнадцати Почему так названы животные
Почему так названы животные ГБоу сош «Школа здоровья» № 883
ГБоу сош «Школа здоровья» № 883 Китайский язык (по учебнику Сизовой А.А.)
Китайский язык (по учебнику Сизовой А.А.) Античный костюм Древней Греции
Античный костюм Древней Греции Недостаток витаминов укорачивает жизнь.
Недостаток витаминов укорачивает жизнь. Отчет по выездной практике
Отчет по выездной практике Малый уголок великой России Диво дивное
Малый уголок великой России Диво дивное Как эффективно убить социальную медиа
Как эффективно убить социальную медиа Автоматы практика
Автоматы практика Как наша прожила б планета Как люди жили бы на ней Без теплоты, магнита, света И электрических лучей!
Как наша прожила б планета Как люди жили бы на ней Без теплоты, магнита, света И электрических лучей! Презентация на тему Династия Романовых
Презентация на тему Династия Романовых Мастера печатных дел
Мастера печатных дел 1 Краткий обзор рекламной активности в группах C02 «Гипотензивные средства» в медицинской прессе и R06 «Антигистаминные средства для
1 Краткий обзор рекламной активности в группах C02 «Гипотензивные средства» в медицинской прессе и R06 «Антигистаминные средства для Исследование Северной Америки
Исследование Северной Америки Эшмоловский музей
Эшмоловский музей Условные предложения
Условные предложения Ice Kit. Доставка мороженого по Москве
Ice Kit. Доставка мороженого по Москве Основные средства организации
Основные средства организации Родительское собрание для групп СПО. Банковское дело. Страховое дело
Родительское собрание для групп СПО. Банковское дело. Страховое дело Презентация на тему Героическая страница моего края
Презентация на тему Героическая страница моего края «Игра на уроках обществознания и права»
«Игра на уроках обществознания и права»