Содержание
- 2. Понятие числа является основным стержнем всего школьного курса математики, пронизывающим этот курс от первого до последнего
- 3. Цель моей работы: рассказать об истории возникновении большинства существующих видов чисел, отдельно рассмотреть комплексные числа, выяснить
- 4. Задачи: 1. Собрать материал по своей теме, «провести» слушателей по всей истории возникновения чисел. 2. Подробно
- 5. Древнегреческие математики считали “настоящими” только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел. Самым
- 6. Позже, в III веке Архимед разработал систему обозначения вплоть до такого громадного как Наряду с натуральными
- 7. Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система
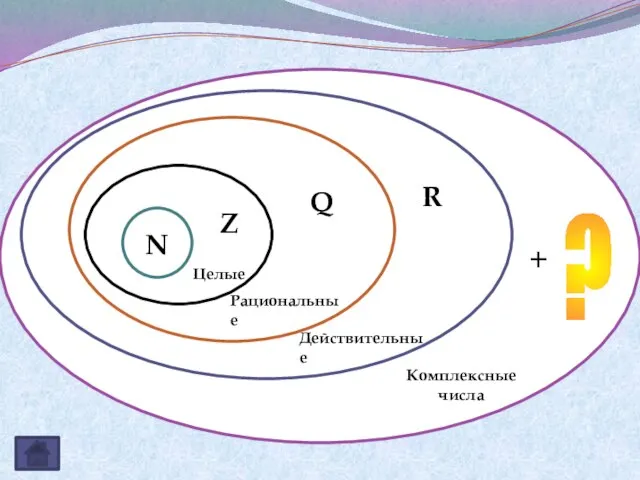
- 8. Комплексные числа N Z Q R Целые Рациональные Действительные
- 9. Исторические факты Впервые мнимые величины появились в работе Дж. Кардано «Великое искусство, или об алгебраических правилах»
- 10. Общий вид комплексного числа: z = a + bi, где a и b – действительные числа,
- 11. Если z = a + bi z = a – bi, то произведением и суммой сопряжённых
- 12. Действия с комплексными числами Сумма: (a + bi) + (c + di) = (a + c)
- 13. Примеры: Найти разность и частное комплексных чисел
- 14. Квадратные уравнения можно решать с помощью комплексных чисел (Если D Например, уравнение: z2 - 3z +
- 15. Модулем комплексного числа называют длину вектора, соответствующего числу. Численно он равен корню из произведения двух сопряженных
- 16. В прямоугольном треугольнике OMN длины катетов ON и OM равны соответственно a и b, а длина
- 17. Тригонометрическая форма записи комплексных чисел Таким образом: z = a + bi = |z| ∙ cos
- 18. Алгебраическая z =a + bi Тригонометрическая z = r (cos φ + i sin φ) Показательная
- 19. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, что |MA|2+|MC|2=|MB|2+|MD|2, то ABCD -
- 20. Формулой Муавра называют выражение, получаемое при возведение комплексного числа в степень n: zn = rn (cos
- 21. Карл Фридрих Гаусс (Gauss) (1777 – 1855) Карл Фридрих Гаусс – немецкий математик. Работы Гаусса оказали
- 22. Леонард Эйлер (Eular) (1707 – 1783) Леонард Эйлер - математик, академик Петербургской академии наук. В его
- 23. Василий Сергеевич Владимиров (1923 – ) Василий Сергеевич - советский и российский математик, академик, Герой Социалистического
- 24. Применение комплексных чисел Сегодня сложно представить себе ряд наук без применения комплексных чисел. Теория электротехники, электромеханики,
- 25. Товар является носителем двух составляющих: потребительских свойств, объективно присущих товару, и цены - денежной оценки потребительских
- 26. Представив какую-либо оценку потребительских свойств товара П как действительную часть комплексного числа, а его цену Ц
- 27. Большой вклад в развитие теории функций комплексной переменной внесли советские ученые: Н. И. Мусхелишвили занимался ее
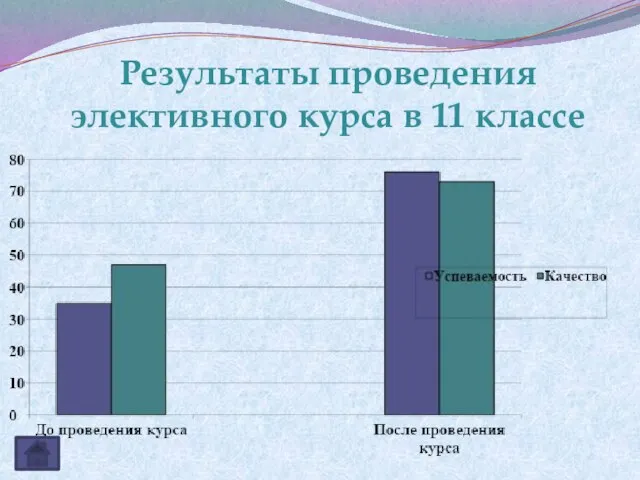
- 28. Результаты проведения элективного курса в 11 классе
- 29. «Мнимые числа – это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием».
- 31. Скачать презентацию


























 Стартовая готовность системы образования Челябинской области к внедрению бережливых технологий
Стартовая готовность системы образования Челябинской области к внедрению бережливых технологий Преподавание истории в старших профильных классах как блок-модуль
Преподавание истории в старших профильных классах как блок-модуль f0bc26d9d99bea8f
f0bc26d9d99bea8f Применение теории игр в политике и экономике
Применение теории игр в политике и экономике Отель Амшенский двор
Отель Амшенский двор Типы и возможности ведения переговоров по странам и континентам
Типы и возможности ведения переговоров по странам и континентам Гжель
Гжель Применение игровых технологий для контроля уровня развития двигательных качеств, умений и знаний на уроках гимнастике
Применение игровых технологий для контроля уровня развития двигательных качеств, умений и знаний на уроках гимнастике Автоматизированные рабочие места
Автоматизированные рабочие места Особливості вступной кампаніи та затвердження
Особливості вступной кампаніи та затвердження  Пневматические схемы тепловозов ТЭМ18ДМ, 2М62, 2ТЭ10М
Пневматические схемы тепловозов ТЭМ18ДМ, 2М62, 2ТЭ10М Административные правоотношения
Административные правоотношения Папка проведение ВВ
Папка проведение ВВ Изделия для ландшафтного дизайна
Изделия для ландшафтного дизайна Органоиды клетки
Органоиды клетки Blagotvoritelny_fond_pomoschi_tyazhelobolnym_detyam
Blagotvoritelny_fond_pomoschi_tyazhelobolnym_detyam ОТЧЕ НАШ…
ОТЧЕ НАШ… Многогранники в природе
Многогранники в природе Тауэр в Лондоне
Тауэр в Лондоне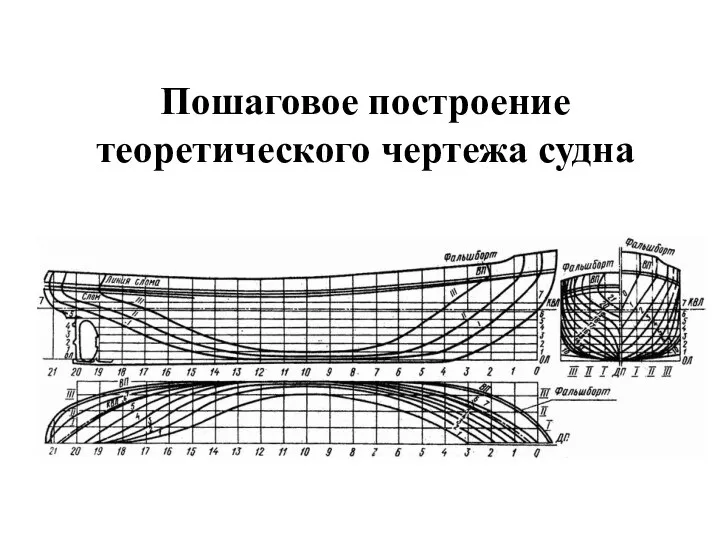 Poshagovoe_postroenie_TCh_sudna (2)
Poshagovoe_postroenie_TCh_sudna (2) Всеукраинский фестиваль инновационных проектов
Всеукраинский фестиваль инновационных проектов Отчет по проделанной работе
Отчет по проделанной работе Расстановка фигур
Расстановка фигур ТЕСТ
ТЕСТ Главные принципы силовой тренировки
Главные принципы силовой тренировки Африканский стиль
Африканский стиль Преза на собру профоргов
Преза на собру профоргов ПЕРЕВОЗКА ДЕНЕГ И ЦЕННОСТЕЙ
ПЕРЕВОЗКА ДЕНЕГ И ЦЕННОСТЕЙ