Презентация на тему Напряженность электрического поля.Теорема Гаусса и потенциал Napryazhennost-elektrostaticheskogo-polya.-Teorema-Gaussa-i-potencial.ppt

10. Электростатика
10.1. Электрические заряды
Единица электрического заряда — кулон (Кл) — электрический заряд, проходящий через попереч­ное сечение проводника при силе тока 1 А за время 1 с.
Электрический заряд (количество электричества) — это физическая величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Все тела в природе способны электризоваться, т. е. приобретать электрический заряд.
Электризация тел может осуществляться различными способами: трением, электростатической индукцией и т. п.

Закон сохранения заряда:
«алгебраическая сумма электрических зарядов любой замкнутой системы остается неизменной». Электрический заряд дискретен. Элементарный электрический заряд е = 1,6⋅10–19 Кл.
Электрон и протон являются носителями элементарных зарядов.
Точечным называется заряд, сосредоточенный на теле, линейные раз­меры которого пренебрежимо малы по сравнению с расстоянием до других заряжен­ных тел.
Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними:
k — коэффициент пропорциональности.

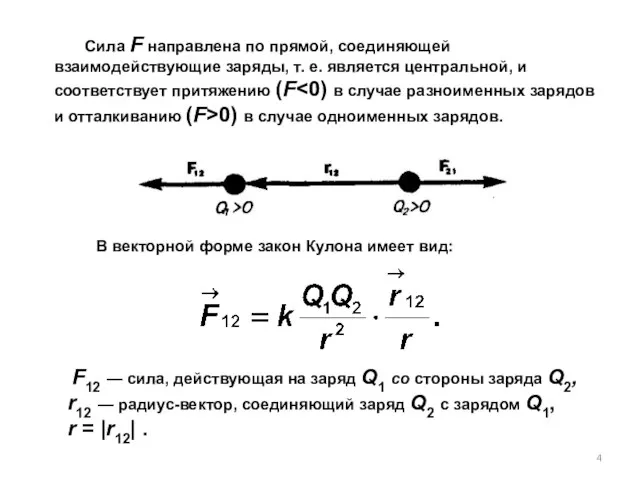
Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов.
В векторной форме закон Кулона имеет вид:
F12 — сила, действующая на заряд Q1 со стороны заряда Q2, r12 — радиус-вектор, соединяющий заряд Q2 с зарядом Q1,
r = |r12| .

В системе СИ коэффициент пропорциональности равен:
С учетом этого закон Кулона запишется в окончательном виде:
Величина ε0 называется электрической постоянной. Она относится к числу фундамен­тальных физических постоянных и равна:
Фарад (Ф) — единица электрической емкости.

10.2. Электростатическое поле.
Напряженность электростатического поля
В пространстве, окружающем неподвижные элект­рические заряды, существует силовое поле. Это поле называ­ются электростатическим.
Силовая характеристика электростатичес­кого поля называется напряженностью и обозначается E.
Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля.

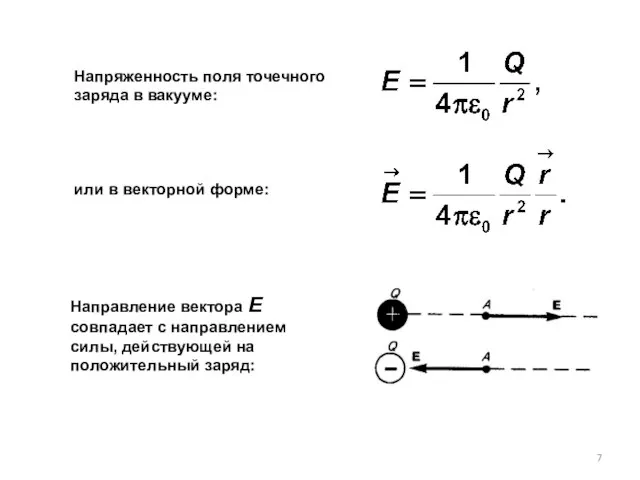
Напряженность поля точечного заряда в вакууме:
Направление вектора Е совпадает с направлением силы, действующей на положитель­ный заряд:
или в векторной форме:

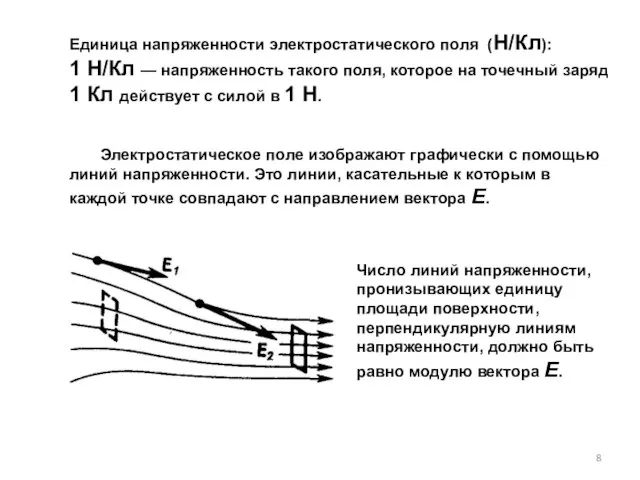
Единица напряженности электростатического по­ля (Н/Кл):
1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н.
Электростатическое поле изображают графически с помощью линий напряженности. Это линии, касательные к которым в каждой точке совпадают с направлением вектора Е.
Число линий напряженности, прони­зывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е.

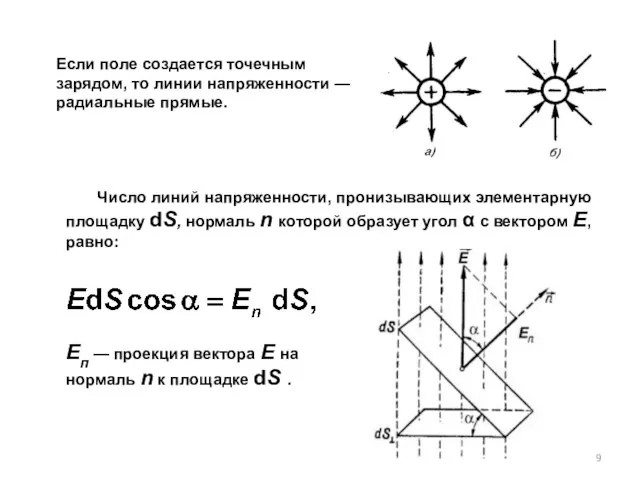
Если поле создается точечным зарядом, то линии напряженности — радиальные прямые.
Число линий напряженности, пронизыва­ющих элементарную площадку dS, нормаль n которой образует угол α с вектором Е, равно:
Еп — проекция вектора Е на нормаль n к площадке dS .

Поток вектора напряженности через площадку dS:
Здесь dS = dSn — век­тор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке
Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверх­ность:
интеграл берется по замкнутой поверхности S.

10.3. Принцип суперпозиции электростатических полей. Поле диполя
Принцип суперпозиции полей позволяет определить модуль и направление вектора напряженности Е в каж­дой точке электростатического поля, создаваемого системой неподвижных зарядов Q1, Q2, ..., Qn.
Принцип суперпозиции (наложения) электростатических полей :
«напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности».

Пример расчета напряженности электростатического поля с помощью метода наложения: расчет напряженности поля диполя.
Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q, –Q), расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля.
Вектор, направленный по оси диполя от отрицательного заряда к положи­тельному и равный расстоянию между ними, называется плечом диполя.
Электрическим моментом диполя или дипольным моментом называется вектор, совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l .
Дипольный момент:

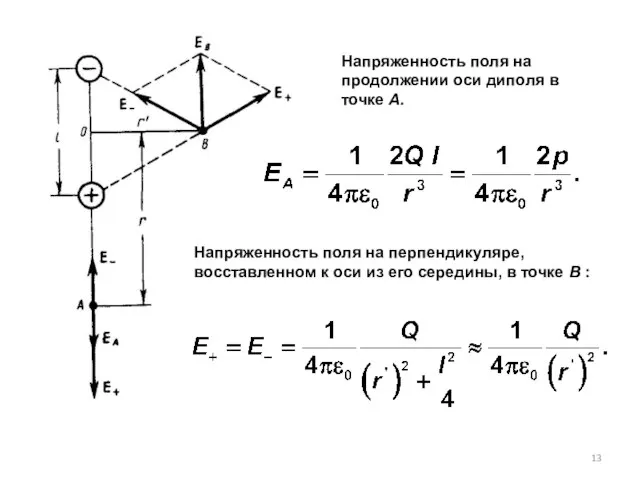
Напряженность поля на продолжении оси диполя в точке А.
Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке В :

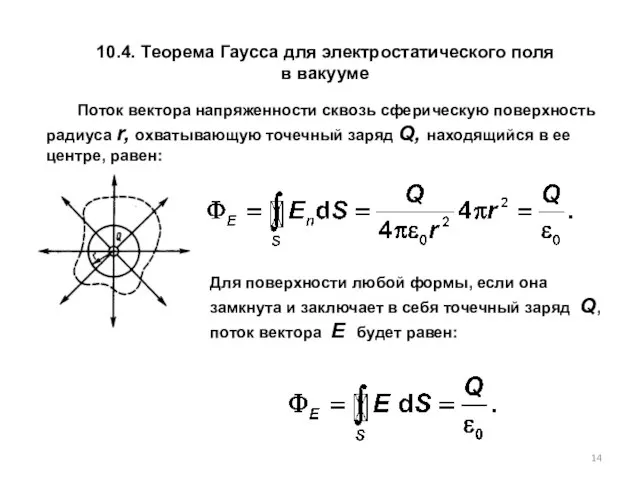
10.4. Теорема Гаусса для электростатического поля в вакууме
Поток вектора напряженности сквозь сферичес­кую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре, равен:
Для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен:

Общий случай произвольной поверхности, окружающей n зарядов.
Каждый из интегралов, стоящих под знаком суммы, равен Qi /ε0, следовательно:
Теорема Гаусса для электростатического поля в вакууме:
«поток вектора напряженности электростатического поля в вакууме сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε0.
- теорема Гаусса.

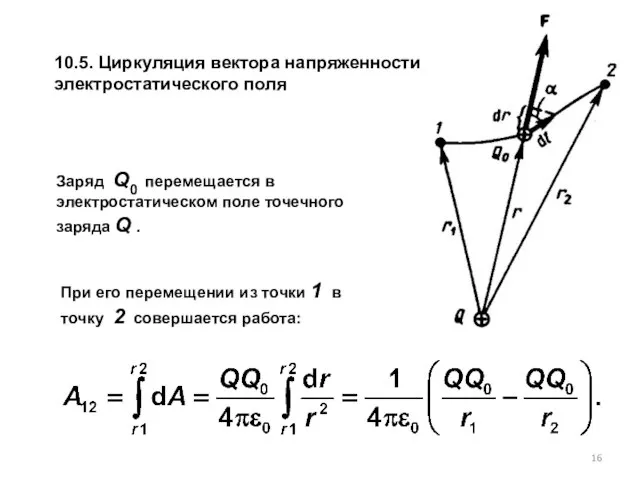
10.5. Циркуляция вектора напряженности электростатического поля
При его перемещении из точки 1 в точку 2 совершается работа:
Заряд Q0 перемещается в электростатическом поле точечного заряда Q .

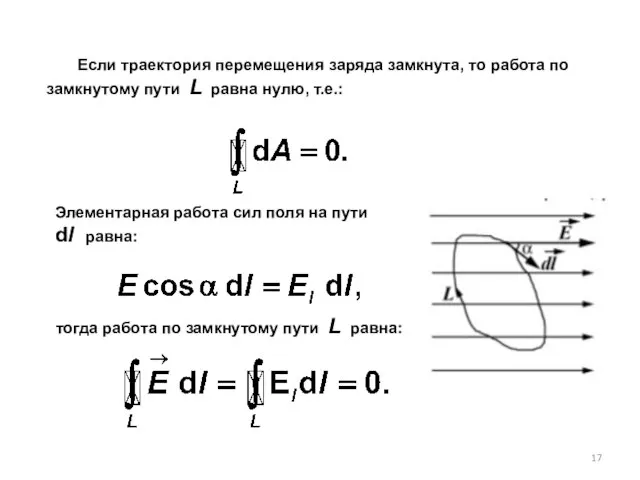
Если траектория перемещения заряда замкнута, то работа по замкнутому пути L равна нулю, т.е.:
Элементарная работа сил поля на пути dl равна:
тогда работа по замкнутому пути L равна:

Интеграл
называется циркуляцией вектора напряженности.
Циркуляция вектора напряженности электростатического поля вдоль любого за­мкнутого контура равна нулю.
Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми.
Они начинаются и кончаются на зарядах или же уходят в бесконечность.

10.6. Потенциал электростатического поля
Работу сил электро­статического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q0 в начальной и конечной точках поля заряда Q:
Потенциальная энергия заряда Q0, находящегося в поле заряда Q на расстоянии r от него, равна:

Отношение потенциальной энергии точечного заряда к его величине называется по­тенциалом: Потенциал ϕ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещен­ного в эту точку.
Потенциал поля, создаваемого точечным зарядом Q, равен:
Если поле создается системой n точечных зарядов Q1, Q2, ..., Qn, то:

Работа сил поля при перемещении заряда Q0 из точки 1 в точку 2 и разность потенциалов этих точек может быть записана через интеграл:
Работа, совершаемая селами электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 :
т. е. разность потенциалов двух точек 1 и 2 определяется работой, совершаемой силами поля, при перемещении единичного поло­жительного заряда из точки 1 в точку 2.

Единица потенциала — вольт (В):
1 В есть потен­циал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл).
Если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
Если перемещать заряд Q0 из произвольной точки за пределы поля в бесконеч­ность, где, по условию, потенциал равен нулю, то:
Потенциал — физическая величина, определяемая работой по переме­щению единичного положительного заряда при удалении его из данной точки поля в бесконечность.

10.7. Напряженность как градиент потенциала. Эквипотенциальные поверхности
Напряженность является силовой характеристикой поля, а потенциал — энергетической характеристикой поля.
.
Работа по перемещению единичного точечного положительного заряда из одной точки поля в другую вдоль оси х :
Работа вдоль осей x, y и z:
i, j, k — единичные векторы координатных осей х, у, z.

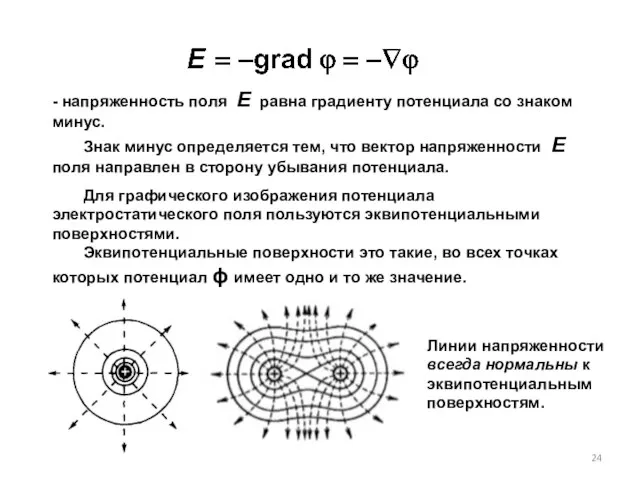
- напряженность поля Е равна градиенту потенциала со знаком минус.
Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.
Для графического изображения потенциала электростатического поля пользуются эквипотенциальными поверхностями.
Эквипотенциальные поверхности это такие, во всех точках которых потенциал ϕ имеет одно и то же значение.
Линии напряженности всегда нормальны к эквипотенциальным поверхностям.

Четыре примера вычисление разности потенциалов по напряженности поля
Поле равномерно заряженной бесконечной плоскости.
σ — поверхностная плотность заряда.
Разность потенциалов между точками, лежащими на расстояниях x1 и х2 от плоскости, равна:

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей.
σ − поверхностная плотность заряда,
d − расстояние между плоскостями.

3. Поле равномерно заряженной сферической поверхности.
Разность потенциалов между двумя точками, лежащими на расстояниях r1 и r2 от центра сферы (r1 >R, r2>R, r2>r1), равна:
Напряженность поля сферической поверхности радиуса R с общим зарядом Q вне сферы (r> R) :

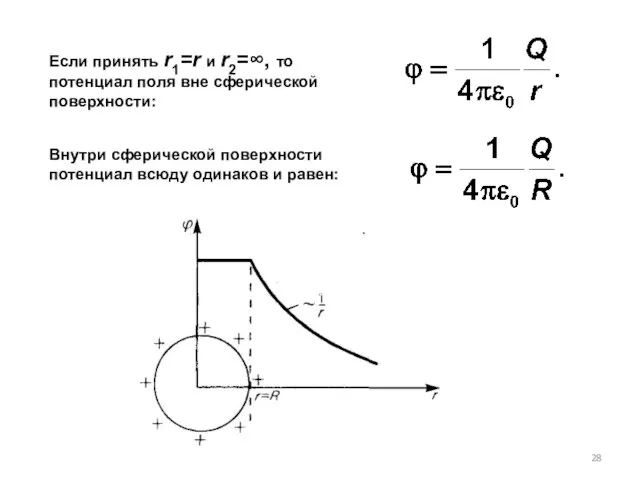
Если принять r1=r и r2=∞, то потенциал поля вне сферической поверхности:
Внутри сферической поверхности потенциал всюду одинаков и равен: