Презентация на тему Решение задач В8 ЕГЭ по математике

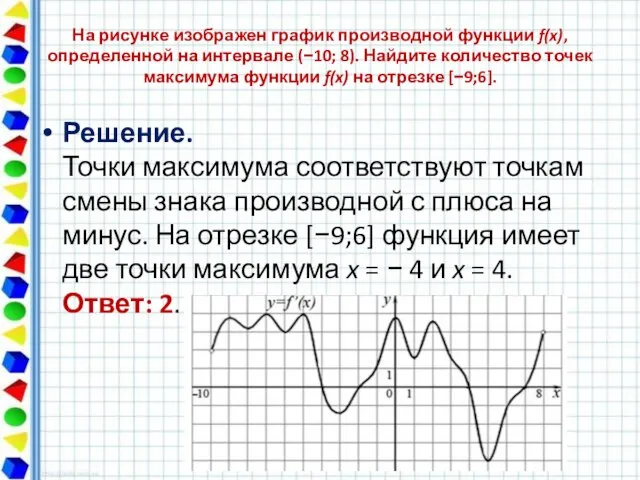
Решение.
Точки максимума соответствуют точкам смены знака производной с плюса на минус. На отрезке [−9;6] функция имеет две точки максимума x = − 4 и x = 4.
Ответ: 2.
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 8). Найдите количество точек максимума функции f(x) на отрезке [−9;6].

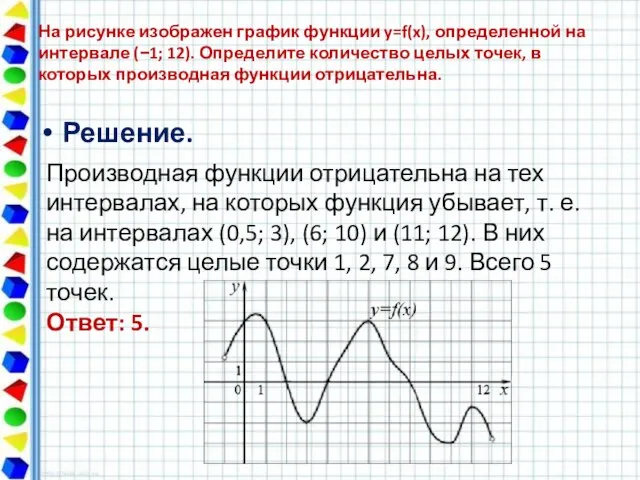
Решение.
На рисунке изображен график функции y=f(x), определенной на интервале (−1; 12). Определите количество целых точек, в которых производная функции отрицательна.
Производная функции отрицательна на тех интервалах, на которых функция убывает, т. е. на интервалах (0,5; 3), (6; 10) и (11; 12). В них содержатся целые точки 1, 2, 7, 8 и 9. Всего 5 точек.
Ответ: 5.

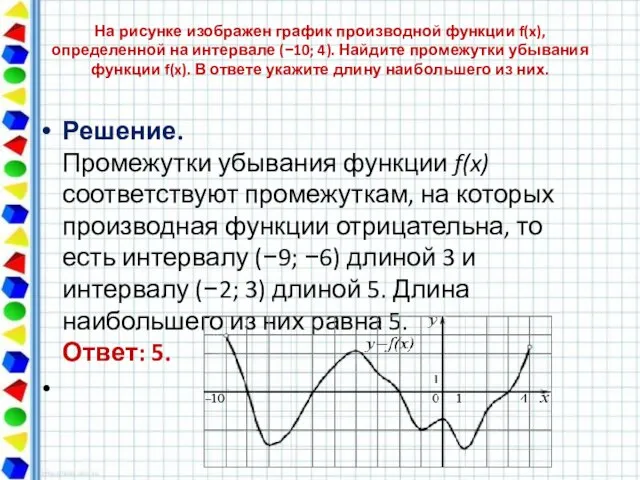
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 4). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Решение.
Промежутки убывания функции f(x) соответствуют промежуткам, на которых производная функции отрицательна, то есть интервалу (−9; −6) длиной 3 и интервалу (−2; 3) длиной 5. Длина наибольшего из них равна 5.
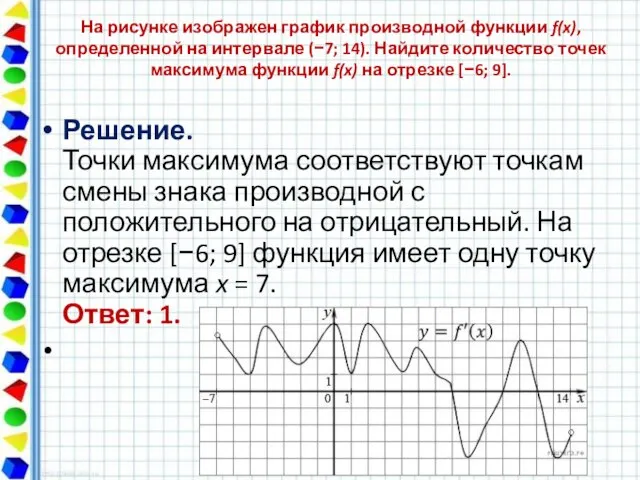
Ответ: 5.

На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].
Решение.
Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [−6; 9] функция имеет одну точку максимума x = 7.
Ответ: 1.

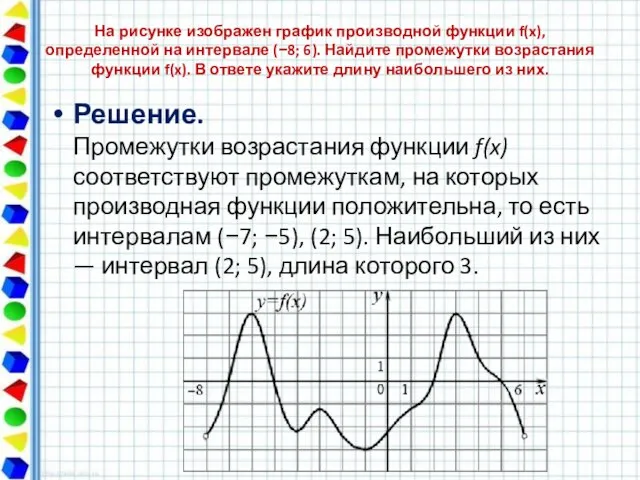
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Решение.
Промежутки возрастания функции f(x) соответствуют промежуткам, на которых производная функции положительна, то есть интервалам (−7; −5), (2; 5). Наибольший из них — интервал (2; 5), длина которого 3.

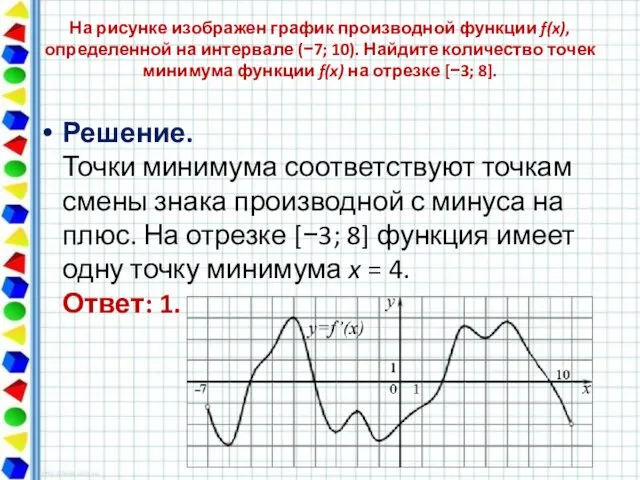
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 10). Найдите количество точек минимума функции f(x) на отрезке [−3; 8].
Решение.
Точки минимума соответствуют точкам смены знака производной с минуса на плюс. На отрезке [−3; 8] функция имеет одну точку минимума x = 4.
Ответ: 1.

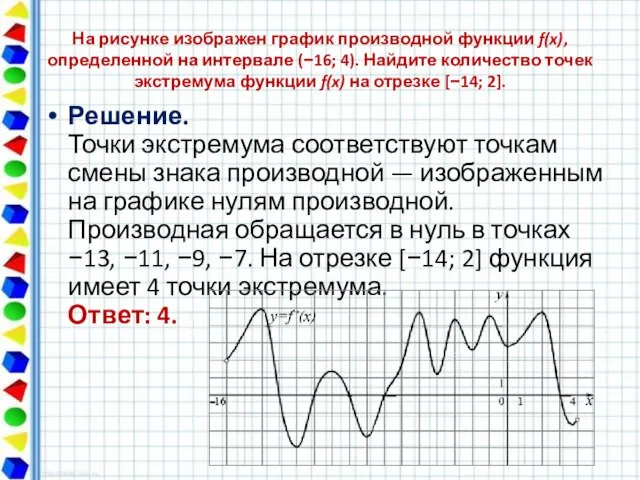
На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции f(x) на отрезке [−14; 2].
Решение.
Точки экстремума соответствуют точкам смены знака производной — изображенным на графике нулям производной. Производная обращается в нуль в точках −13, −11, −9, −7. На отрезке [−14; 2] функция имеет 4 точки экстремума.
Ответ: 4.

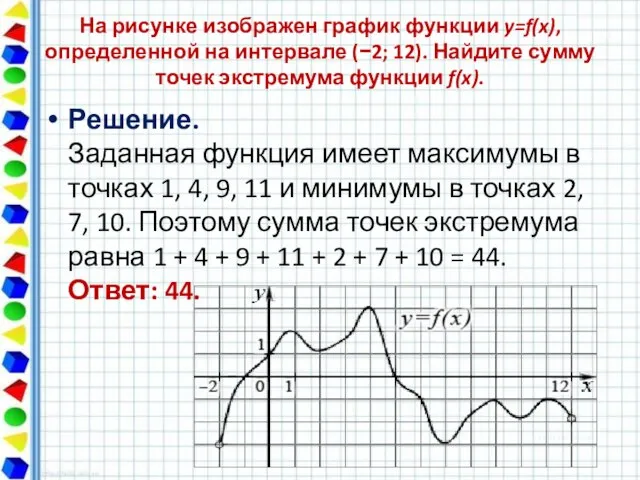
На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
Решение.
Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.
Ответ: 44.

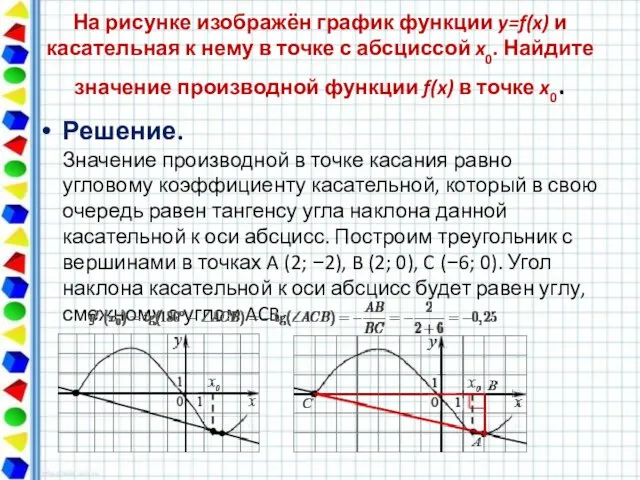
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB

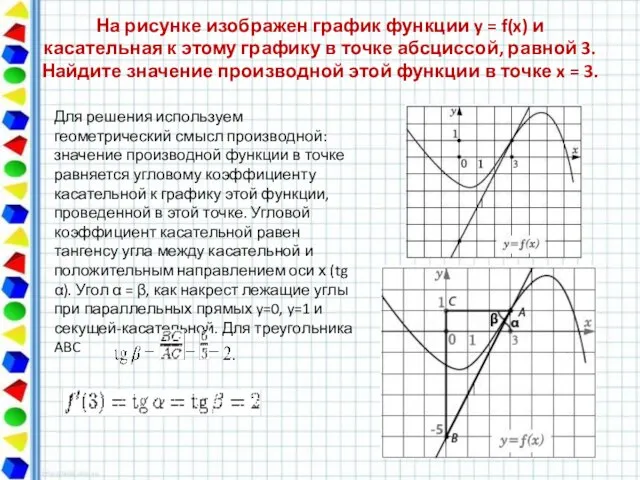
На рисунке изображен график функции y = f(x) и касательная к этому графику в точке абсциссой, равной 3. Найдите значение производной этой функции в точке x = 3.
Для решения используем геометрический смысл производной: значение производной функции в точке равняется угловому коэффициенту касательной к графику этой функции, проведенной в этой точке. Угловой коэффициент касательной равен тангенсу угла между касательной и положительным направлением оси х (tg α). Угол α = β, как накрест лежащие углы при параллельных прямых y=0, y=1 и секущей-касательной. Для треугольника ABC

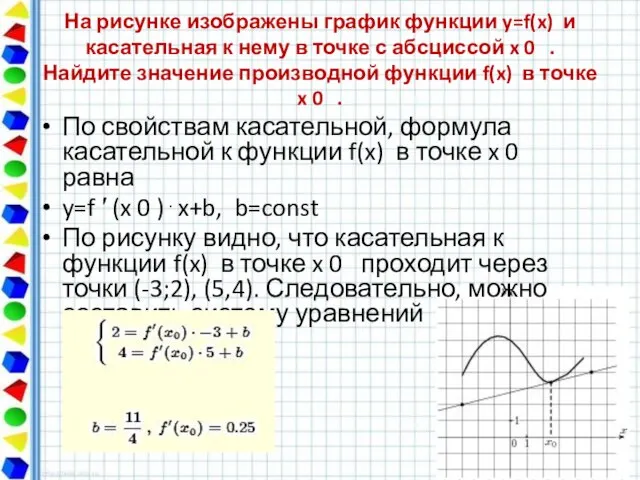
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .
По свойствам касательной, формула касательной к функции f(x) в точке x 0 равна
y=f ′ (x 0 )⋅x+b, b=const
По рисунку видно, что касательная к функции f(x) в точке x 0 проходит через точки (-3;2), (5,4). Следовательно, можно составить систему уравнений