Презентация по математике на тему_ _В мире римских чисел_ (5 класс)

Цели мероприятия:
1. Получение дополнительной информации о римских числах;
2.развитие логического мышления;
3. раскрытие творческих способностей ребенка;
4. привитие интереса к предмету.

ПОЗНАВАТЕЛЬНАЯ ИНФОРМАЦИЯ О РИМСКИХ ЦИФРАХ

В древние времена люди пользовались для счета пальцами, поэтому римские цифры похожи на пальчики. Обратите внимание, как при помощи рук изображаются числа пять и десять – ведь на одной руке 5 пальцев, а на двух – 10. Посмотри на рисунки и обведи римские цифры. В квадратики впиши соответствующие арабские цифры.

Промежуточные числа образовывались путем прибавления нескольких букв справа или слева. Сначала писались тысячи и сотни, затем десятки и единицы. Таким образом, число 24 изображалось как XXIV. Горизонтальная линия над символом означала умножение на тысячу.

Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц.
II, III - четырехкратное повторение любой цифры запрещено.
Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления – после, например:
4 = IV 6 = VI 7 = VII

Та же логика действует и с другими цифрами IX = 9 XL = 40 90 = XC CM = 900
Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888.
888 = DCCCLXXXVIII
(500+100+100+100+50+10+10+10+5+1+1+1)

Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты
IIII и VIIII вместо IV и IX, и даже
IIIII или XXXXXX вместо V и LX.
Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII.
Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). 0 = N

ПРОИСХОЖДЕНИЕ РИМСКИХ ЦИФР
На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки.

Таким образом, цифра «I» - это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х
Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX.
Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику.

Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.

Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру.

Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита.

ПРИМЕНЕНИЕ РИМСКИХ ЦИФР
В русском языке римские цифры используются в следующих случаях:
Номер века или тысячелетия: XIX век, II тысячелетие до н. э.
Порядковый номер монарха
Номер корпуса в Вооруженных силах
ВЕК
I

Номер тома в многотомной книге (иногда — номера частей книги, разделов или глав);
В некоторых изданиях — номера листов с предисловием к книге, чтобы не исправлять ссылки внутри основного текста при изменении предисловия;
Маркировка циферблатов часов «под старину;

Иные важные события или пункты списка, например:
V постулат Евклида,
II мировая война,
Xx съезд КПСС,
Игры XXII Олимпиады и т. п.

Валентность химических элементов.
Порядковый номер ступени в звукоряде.
База гомеопатических разведений (Conium X3, Aconitum C200 и т. п.).
В математическом анализе римскими цифрами иногда записывается номер производной выше третьей.
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).

МНЕМОНИЧЕСКИЕ ПРАВИЛА
Соответственно M, D, C, L, X, V, I
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
M – 1000, D – 500, C – 100, L – 50,
X – 10, X – 10 , V – 5, I - 1
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам

ЗАДАЧКИ, РЕБУСЫ, ГОЛОВОЛОМКИ
Задачи со спичками. И не просто задачи со спичками, а еще и с римскими цифрами. Но не бойтесь: от вас не потребуется никаких специфических знаний или умения составлять длинные римские цифры. Только смекалка. Одна смекалка и несколько спичек.

ЗАДАЧА С ТРЕМЯ СПИЧКАМИ
Итак, берем одну спичку и видим, что с ее помощью мы можем изобразить лишь единицу:
Далее: возьмем две спички и уже, манипулируя с двумя, получаем целых четыре числа, записанных римскими цифрами:
Возьмем 3 спички. Вопрос.
Сколько чисел римских можно составить из 3 спичек?
Должно получиться 7 вариантов.
Думаем…
???

ГОЛОВОЛОМКА «БОКАЛ С ВИШЕНКОЙ
С помощью четырех спичек сложена форма бокала, внутри которого лежит вишня. Нужно передвинуть две спички так, чтобы вишня оказалась за пределами бокала. Разрешается менять положение бокала в пространстве, однако его форма должна оставаться неизменной.

ОСТАВИТЬ 1 ТРЕУГОЛЬНИК
Передвиньте 1 спичку так, чтобы вместо 9 треугольников остался только один.

РАЗВЕРНУТЬ РЫБКУ
Переставьте три спички так, чтобы рыбка поплыла в обратном направлении. Другими словами, нужно повернуть рыбу на 180 градусов по горизонтали.

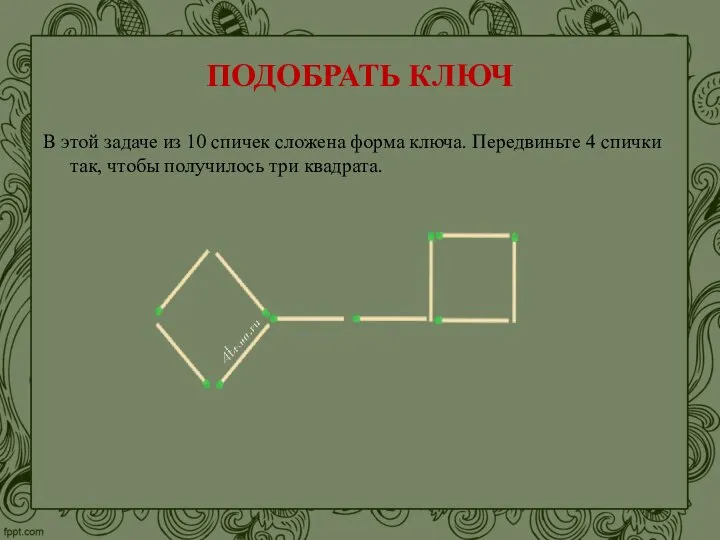
ПОДОБРАТЬ КЛЮЧ
В этой задаче из 10 спичек сложена форма ключа. Передвиньте 4 спички так, чтобы получилось три квадрата.

СЕМЬ КВАДРАТОВ
Переложите 2 спички так, чтобы образовать 7 квадратов.
Соприкасающиеся друг с другом спички. Необходимо разместить 6 спичек так, чтобы каждая спичка соприкасалась с остальными пятью.

ПОЛЕ ДЛЯ КРЕСТИКОВ - НОЛИКОВ
Необходимо переложить 3 спички так, чтобы получить ровно 3 квадрата.
Нужно переместить только одну спичку в выложенном спичками арифметическом примере «8+3-4=0» так, чтобы получилось верное равенство (можно менять и знаки, цифры).

ЗАДАЧКИ СО СПИЧКАМИ
Задача 1
Перенесите одну спичку, чтобы данное выражение стало верным: 6-4=3.
Задача 2
Переложите одну спичку, чтобы данное равенство стало верным: 7-5=7.
Задача 3
Переставьте одну спичку, для того чтобы равенство стало верным: 3+0=8.
Задача 4
. Переставьте 1 спичку, для того чтобы данное выражение стало верным: 4-5=1.
Задача 5
Передвиньте одну спичку, для того чтобы данное равенство стало верным: 1+8=1.
Задача 6
Передвиньте одну спичку, чтобы выражение стало верным: 5+7=7.