Применение свойств квадратичной функции

Задачи на определение числа корней квадратного уравнения.
П р и м е р 1. Имеет ли корни уравнение
1716х2 – 5321х + 3248 = 0?
Решение.
D = 53212 – 4 · 1716 · 3248 > 5000 · 5000 –
– 4 · 1750 · 3250 = 5000 · 5000 – 2 · 1750 · 2 · 3250 =
= 25 000 000 – 3500 · 6500 =
= 25 000 000 – 22 750 000 > 0.
Так как дискриминант положителен, то уравнение имеет два корня.
Рассмотрим функцию f(х) = 1716х2 – 5321х + 3248.
Пусть х = 1, тогда
f(х) = 1716 – 5321 + 3248 < 1800 + 3300 – 5321 < 0.
Это означает, что парабола опускается
ниже оси х. Поэтому она пересекает
ось х в двух точках, а значит, данное
уравнение имеет два корня.

Задачи на определение числа корней квадратного уравнения.
П р и м е р 2. Сколько корней имеет уравнение
(х – 100)(х – 101) + (х – 101)(х – 102) + (х – 102)(х – 100) = 0? Решение. Раскроем скобки в левой части и представим
её в виде квадратного трехчлена с положительным
коэффициентом при х2. Обозначим этот трехчлен через
f(х). Найдем f(101):
f(101) = 0 + 0 – 1 < 0.
Таким образом, трехчлен f(х) может принимать
отрицательные значения. Так как коэффициент при х2
положителен, то ветви параболы направлены вверх.
Значит, парабола пересекает ось х в двух точках, т. е.
данное уравнение имеет два корня.

Примеры на определение местонахождения корней квадратного уравнения на числовой прямой.
П р и м е р 3. Докажем, что один из корней уравнения
52х2 – 70х + 15 = 0 больше 1, а другой меньше 1.
Решение. Докажем, что число 1 лежит между корнями данного уравнения. Возьмем функцию f(х) = 52х2 – 70х + 15 и найдем f(1):
f(1) = 52 – 70 + 15 < 0.
Функция у = f(х) может принимать
отрицательные значения. Таким образом,
график функции f(х) — парабола, ветви
которой направлены вверх и которая
опускается ниже оси х. Отрицательные значения эта функция
принимает в промежутке между корнями. Так как f(1) < 0,
то х1 < 1 < х2.

Примеры на определение местонахождения корней квадратного уравнения на числовой прямой.
П р и м е р 4. Установить, как на координатной оси расположены числа:
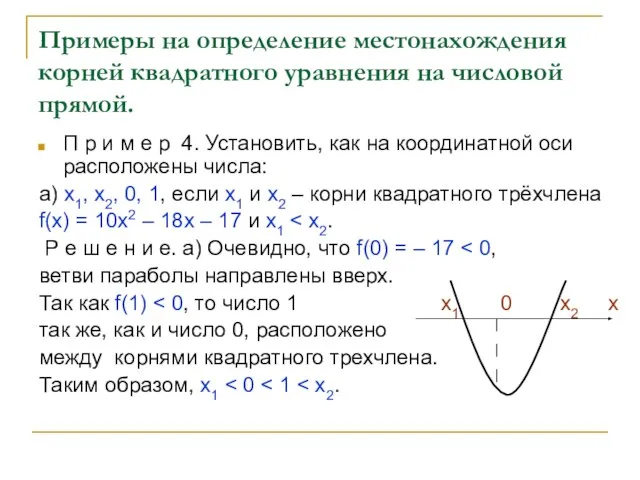
а) х1, х2, 0, 1, если х1 и х2 – корни квадратного трёхчлена
f(х) = 10х2 – 18х – 17 и х1 < х2.
Р е ш е н и е. а) Очевидно, что f(0) = – 17 < 0,
ветви параболы направлены вверх.
Так как f(1) < 0, то число 1 х1 0 х2 х
так же, как и число 0, расположено
между корнями квадратного трехчлена.
Таким образом, х1 < 0 < 1 < х2.

Примеры на определение местонахождения корней квадратного уравнения на числовой прямой.
П р и м е р 4. Установить, как на координатной оси расположены числа:
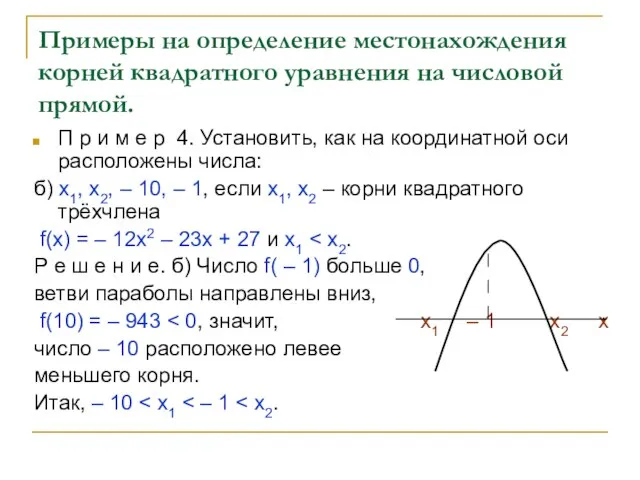
б) х1, х2, – 10, – 1, если х1, х2 – корни квадратного трёхчлена
f(х) = – 12х2 – 23х + 27 и х1 < х2.
Р е ш е н и е. б) Число f( – 1) больше 0,
ветви параболы направлены вниз,
f(10) = – 943 < 0, значит, х1 – 1 х2 х
число – 10 расположено левее
меньшего корня.
Итак, – 10 < х1 < – 1 < х2.

Решение физических задач с применением свойств квадратичной функции.
П р и м е р 5. Мяч подброшен вертикально вверх. Зависимость
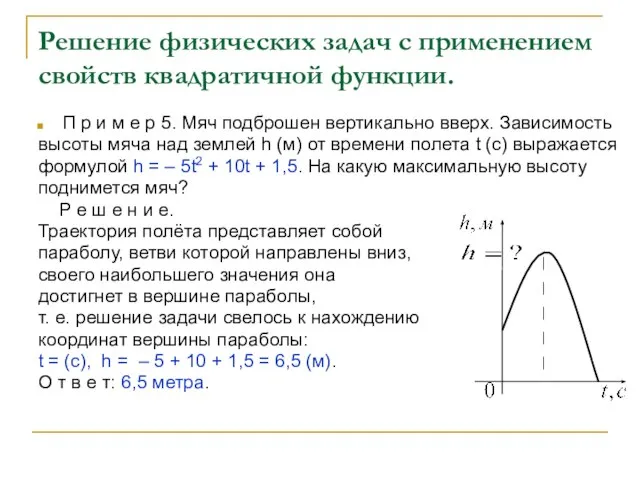
высоты мяча над землей h (м) от времени полета t (с) выражается
формулой h = – 5t2 + 10t + 1,5. На какую максимальную высоту
поднимется мяч?
Р е ш е н и е.
Траектория полёта представляет собой
параболу, ветви которой направлены вниз,
своего наибольшего значения она
достигнет в вершине параболы,
т. е. решение задачи свелось к нахождению
координат вершины параболы:
t = (с), h = – 5 + 10 + 1,5 = 6,5 (м).
О т в е т: 6,5 метра.

Решение физических задач с применением свойств квадратичной функции.
П р и м е р 6. Камень брошен вертикально вверх. Пока
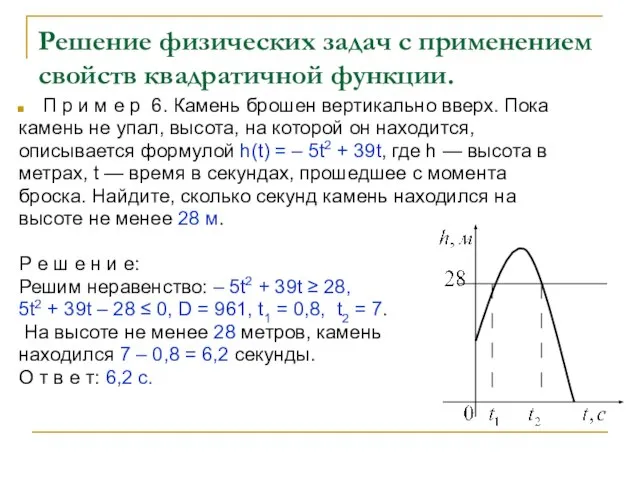
камень не упал, высота, на которой он находится,
описывается формулой h(t) = – 5t2 + 39t, где h — высота в
метрах, t — время в секундах, прошедшее с момента
броска. Найдите, сколько секунд камень находился на
высоте не менее 28 м.
Р е ш е н и е:
Решим неравенство: – 5t2 + 39t ≥ 28,
5t2 + 39t – 28 ≤ 0, D = 961, t1 = 0,8, t2 = 7.
На высоте не менее 28 метров, камень
находился 7 – 0,8 = 6,2 секунды.
О т в е т: 6,2 с.