Содержание
- 2. Определения В математическом смысле проекции - это преобразования точек пространства размерности n в точки пространства размерности
- 3. Мировые и экранные координаты мировые координаты, которые описывают истинное положение объектов в пространстве с заданной точностью.
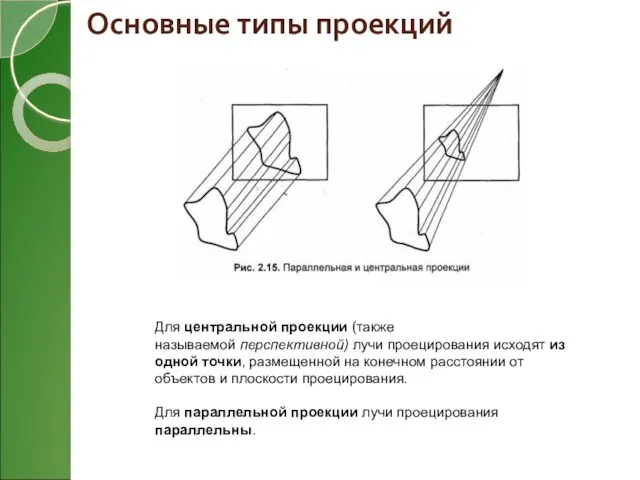
- 4. Основные типы проекций Для центральной проекции (также называемой перспективной) лучи проецирования исходят из одной точки, размещенной
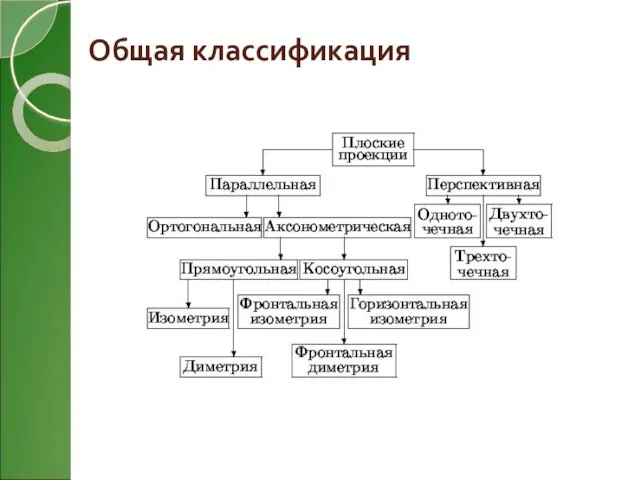
- 5. Общая классификация
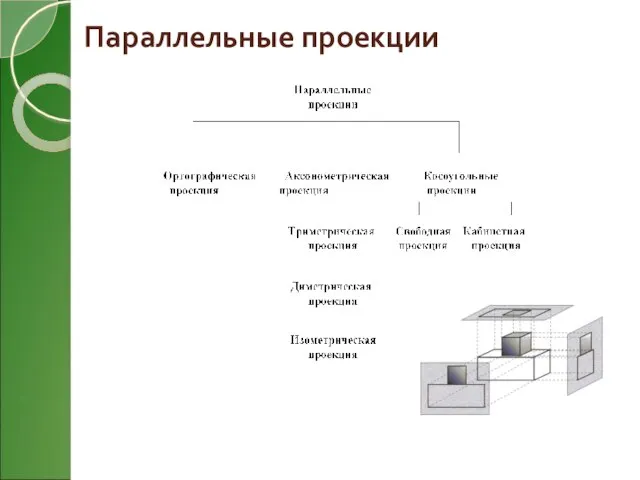
- 6. Параллельные проекции
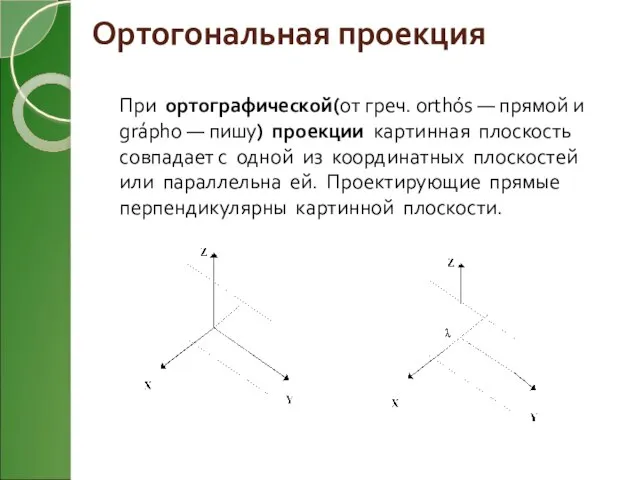
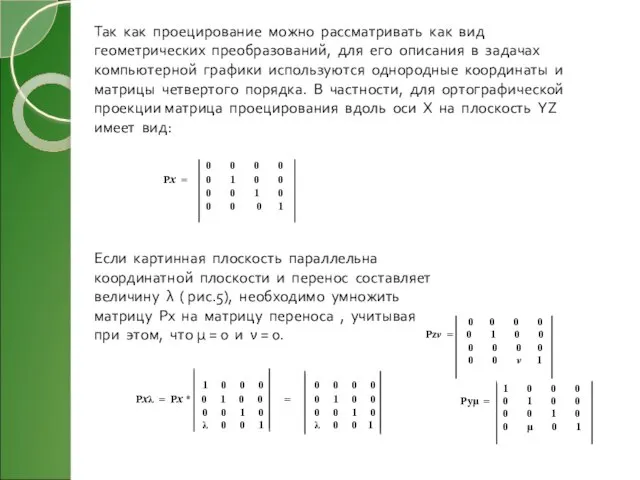
- 7. Ортогональная проекция При ортографической(от греч. orthós — прямой и grápho — пишу) проекции картинная плоскость совпадает
- 8. 0 0 0 0 Px = 0 1 0 0 0 0 1 0 0 0
- 9. Аксонометрические проекции Аксонометрические проекции подразделяются на три группы в соответствии с расположением проекционной плоскости по отношению
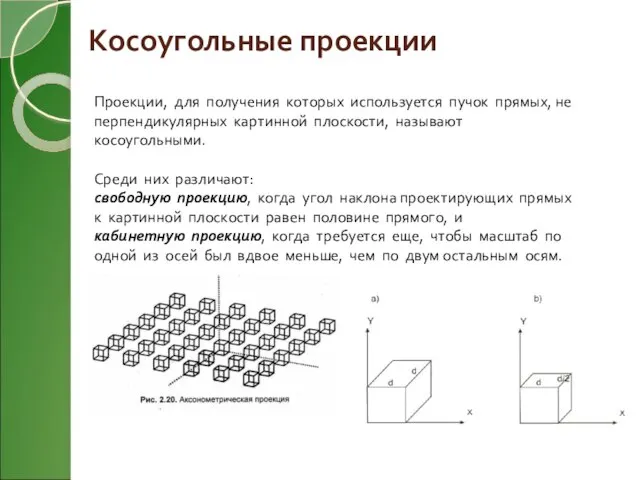
- 10. Косоугольные проекции Проекции, для получения которых используется пучок прямых, не перпендикулярных картинной плоскости, называют косоугольными. Среди
- 11. Представление Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проецирование. Так,
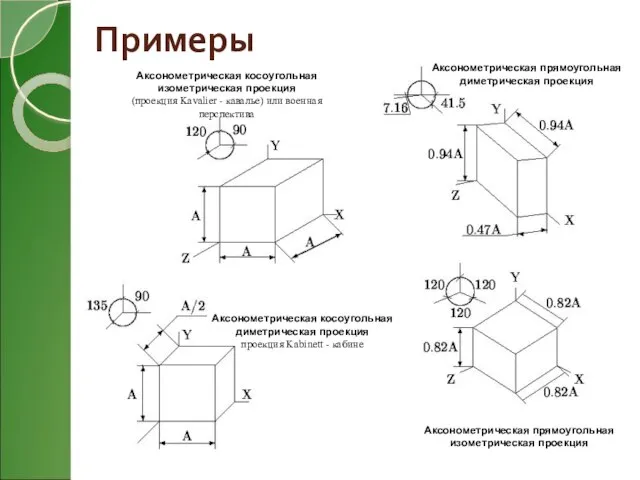
- 12. Примеры Аксонометрическая прямоугольная изометрическая проекция Аксонометрическая прямоугольная диметрическая проекция Аксонометрическая косоугольная диметрическая проекция проекция Kabinett -
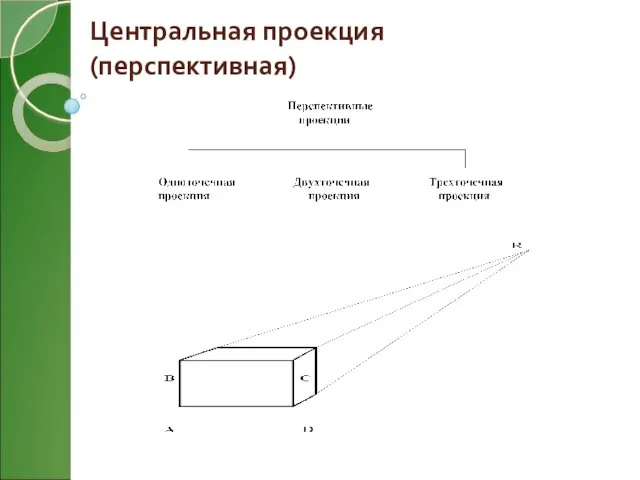
- 13. Центральная проекция (перспективная)
- 14. Описание Эффект перспективы заключается в том, что параллельные прямые пересекаются на горизонте (рис.1). Предметы должны становиться
- 15. Свойства перспективной проекции: 1. Перспективная проекция прямой линии есть прямая линия. 2. Перспективная проекция грани (то
- 16. Представление 1 0 0 0 Q = 0 1 0 0 0 0 0 - 1
- 17. Алгоритм вычисления перспективной проекции Учитывая все сказанное выше о перспективных проекциях можно отметить следующее: 1. Каждую
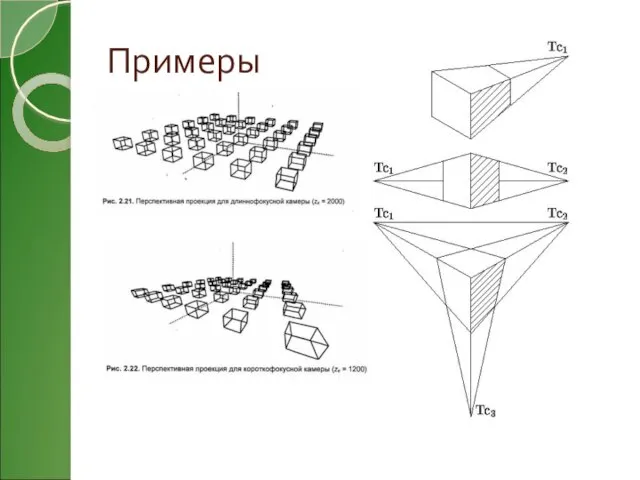
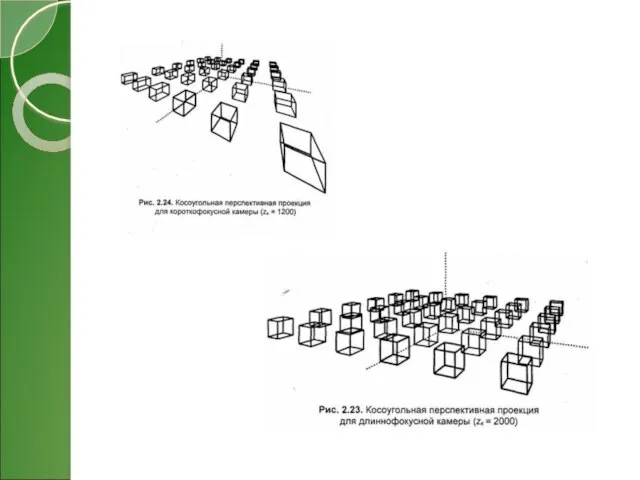
- 18. Примеры
- 21. Скачать презентацию








 Законодательство Республики Казахстан в области информационной безопасности
Законодательство Республики Казахстан в области информационной безопасности Духи
Духи Обобщение темы«Тепловые явления»
Обобщение темы«Тепловые явления» Каникулы
Каникулы Родительское собрание
Родительское собрание П рофильное обучение в старших классах, ориентированно на индивидуализацию обучения и социализацию обучающихся (с учетом реальны
П рофильное обучение в старших классах, ориентированно на индивидуализацию обучения и социализацию обучающихся (с учетом реальны Зима в парке
Зима в парке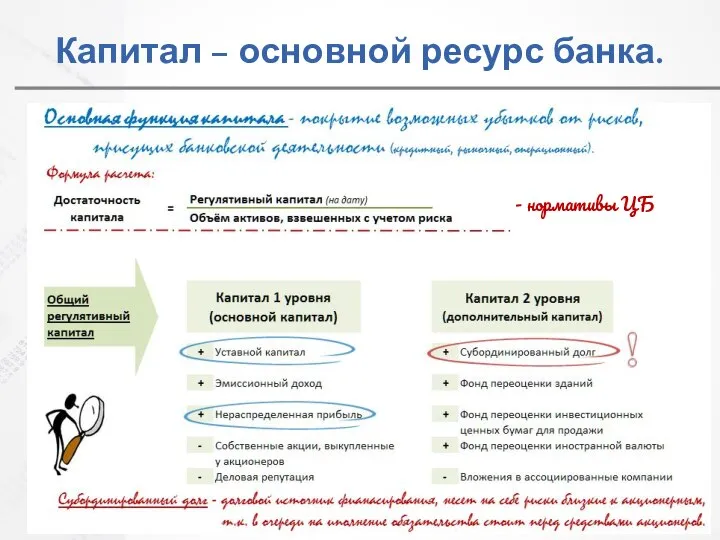 Капитал - основной ресурс банка. Формулы
Капитал - основной ресурс банка. Формулы Hyundai Sonata2.7V6сравнение с конкурентами
Hyundai Sonata2.7V6сравнение с конкурентами Кристаллические тела 10 класс
Кристаллические тела 10 класс Глава №9. Международные сопоставления ВВП и его компонентов на основе паритетов покупательской способности валют
Глава №9. Международные сопоставления ВВП и его компонентов на основе паритетов покупательской способности валют Презентация на тему Каменный уголь
Презентация на тему Каменный уголь  РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК
РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК Выколотка. Чеканка. Гравировка
Выколотка. Чеканка. Гравировка Презентация на тему «История создания Linux»
Презентация на тему «История создания Linux» Презентация на тему Лес наш друг
Презентация на тему Лес наш друг  Презентация на тему Русско-японская война 1904-1905 гг
Презентация на тему Русско-японская война 1904-1905 гг  Презентация на тему Английские колонии в Северной Америке 7 класс
Презентация на тему Английские колонии в Северной Америке 7 класс Мãн Хураçкари пĕтемĕшле пĕлӳ паракан тĕп шкул
Мãн Хураçкари пĕтемĕшле пĕлӳ паракан тĕп шкул Презентация на тему Famous British Writers (Знаменитые британские писатели)
Презентация на тему Famous British Writers (Знаменитые британские писатели)  ЗАБЕЗПЕЧЕННЯ ДОСТУПУ ДО ПУБЛІЧНОI ІНФОРМАЦІI
ЗАБЕЗПЕЧЕННЯ ДОСТУПУ ДО ПУБЛІЧНОI ІНФОРМАЦІI Црква у хришћанској архитектури
Црква у хришћанској архитектури Природные зоны. Лес. Растения леса
Природные зоны. Лес. Растения леса Краткое описание ресурса Одни из немногих футбольных интернет ресурсов на территории Украины, который подает информацию на 2-х язы
Краткое описание ресурса Одни из немногих футбольных интернет ресурсов на территории Украины, который подает информацию на 2-х язы My favourite city. Шаблон
My favourite city. Шаблон Презентация на тему Литература Древней Руси
Презентация на тему Литература Древней Руси urok-povtoreniya-po-kursu-obschestvoznaniya-dlya-7
urok-povtoreniya-po-kursu-obschestvoznaniya-dlya-7 Современное искусство Египта
Современное искусство Египта