Проецирование точки

ПРОЕЦИРОВАНИЕ ТОЧКИ

Проекцией точки на плоскости называется точка пересечения с этой плоскостью перпендикуляра, опущенного из данной точки. Изложенный способ получения проекции точки называется прямоугольным проецированием на плоскость.
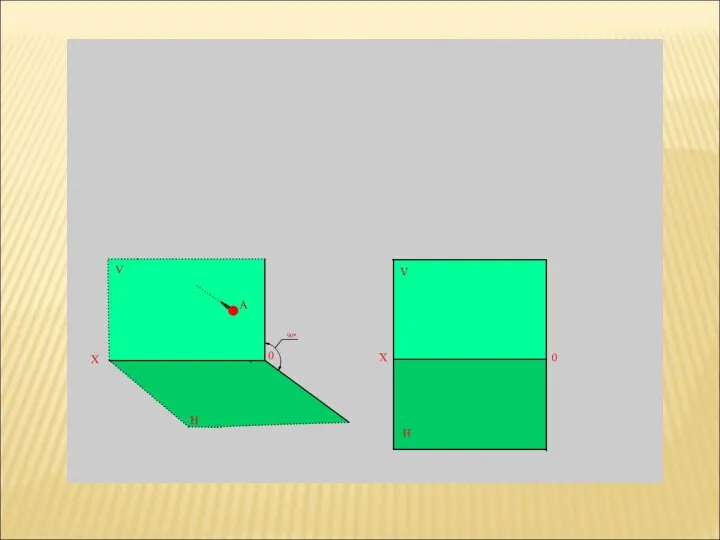
По одной проекции точки а на плоскости Н нельзя определить положение самой точки в пространстве, для этого берут не одну , а две взаимно пересекающиеся под прямым углом плоскости проекций - H и V. Для получения прямоугольных проекций точки А ее проецируют на плоскости H и V, опуская на них из точки А проецирующие прямые. При этом получают две проекции точки А: горизонтальную а на плоскости H и фронтальную а’ на плоскости V.

Чтобы получить изображение точки А в виде чертежа,поворачивают плоскость проекций H вместе с горизонтальной проекцией а внизвокруг оси ОХ до совмещения с плоскостью V. Проекции точки А, полученные на плоскостях проекций в совмещенном их положении, оказываются расположенными одна под другой. Проекции проецирующих прямых а’ах и аах, перпендикулярные к оси проекций ОХ, имея одну общую точку ах, составляют прямую линию а’ ах а, перпендикулярную к оси проекций ОХ.

Вывод: в совмещенном положении двух плоскостей H и V обе проекции точки всегда лежат на одном перпендикуляре к оси ОХ.