Содержание
- 2. Общие сведения о передачах Определение: Передача − устройство, предназначенное для передачи энергии из одной точки пространства
- 3. Классификация механических передач вращательного движения (2 слайда): 1. По способу передачи движения от входного вала к
- 4. 4. По характеру изменения передаточного отношения (числа): передачи с постоянным (неизменным) передаточным отношением и передачи с
- 5. Главные характеристики передач (2 слайда): мощности на входном и выходном валах - Pвх, Pвых; и их
- 6. Сумма коэффициентов полезного действия и потерь всегда равна единице: (2.4) Для многоступенчатой передачи, включающей k последовательно
- 7. Окружная (касательная) скорость в любой точке вращающегося элемента (колеса, шкива, вала), лежащей на диаметре D этого
- 8. В технических расчетах (особенно прочностных) направление вращения чаще всего не имеет решающего значения. В таких расчетах
- 9. Определение: Ременная передача – это механизм, предназначенный для передачи вращательного движения посредством фрикционного взаимодействия или зубчатого
- 10. Достоинства ременных передач: 1. Простота конструкции и низкая стоимость. 2. Возможность передачи движения на достаточно большие
- 11. Классификация ременных передач (2 слайда): 1. По форме поперечного сечения ремня: 1.1 плоскоременные (поперечное сечение ремня
- 12. 3. По числу и виду шкивов, применяемых в передаче: 3.1 с одношкивными валами; 3.2 с двушкивным
- 13. При расчетах клиноременных передач для ведущего и ведомого шкивов используются расчетные диаметры dр1 и dр2. Угол
- 14. а так как этот угол обычно невелик, то во многих расчетах допустимым является приближение γ ≈
- 15. . (2.17) С целью обеспечения стабильности работы передачи обычно принимают для плоского ремня − , а
- 16. Силовые соотношения в ременной передаче. В ременной передаче силы нормального давления между поверхностями трения можно создать
- 17. Для ремня, охватывающего шкив, по формуле Эйлера F1=F2⋅ e f⋅α, где e – основание натурального логарифма
- 18. Кинематика ременной передачи. Удлинение каждого отдельно взятого элемента ремня меняется в зависимости от того, на какую
- 19. где индекс «1» соответствует ведущему, а индекс «2» − ведомому шкивам. Передаточное число ременной передачи, представленное
- 20. Напряжения в ремне. В ремне возникают напряжения от действия рабочей нагрузки, от изгиба вокруг шкива, от
- 21. Особенности конструкции, работы и расчета клиноременных и поликлиноременных передач. Клиновые ремни имеют трапециевидное поперечное сечение, а
- 22. Размеры сечений клиновых ремней стандартизованы (ГОСТ 1284.1-89, ГОСТ 1284.2-89, ГОСТ 1284.3-89). Стандартом предусмотрено 7 ремней нормального
- 24. Скачать презентацию
Слайд 2Общие сведения о передачах
Определение:
Передача − устройство, предназначенное для передачи энергии из одной
Общие сведения о передачах
Определение:
Передача − устройство, предназначенное для передачи энергии из одной

В зависимости от вида передаваемой энергии передачи: механические, электрические, гидравлические, пневматические и т.п.
Механическая передача − устройство (механизм, агрегат), предназначенное для передачи энергии механического движения, как правило, с преобразованием его кинематических и силовых параметров, а иногда и самого вида движения.
Наибольшее распространение в технике получили механические передачи вращательного движения, которым в курсе деталей машин уделено основное внимание (далее под термином передача подразумевается, если это не оговорено особо, именно механическая передача вращательного движения).
Слайд 3Классификация механических передач вращательного движения (2 слайда):
1. По способу передачи движения от
Классификация механических передач вращательного движения (2 слайда):
1. По способу передачи движения от

1.1. Передачи зацеплением:
1.1.1. с непосредственным контактом тел вращения − зубчатые, червячные, винтовые;
1.1.2. с гибкой связью − цепные, зубчато-ременные.
1.2. Фрикционные передачи:
1.2.1. с непосредственным контактом тел вращения – фрикционные;
1.2.2. с гибкой связью - ременные.
2. По взаимному расположению валов в пространстве:
2.1. с параллельными осями валов − зубчатые с цилиндрическими колесами, фрикционные с цилиндрическими роликами, цепные;
2.2. с пересекающимися осями валов - зубчатые и фрикционные конические, фрикционные лобовые;
2.3. с перекрещивающимися осями - зубчатые - винтовые и коноидные, червячные, лобовые фрикционные со смещением ролика.
3. По характеру изменения угловой скорости выходного вала по отношению к входному: редуцирующие (понижающие) и мультиплицирующие (повышающие).
Слайд 44. По характеру изменения передаточного отношения (числа): передачи с постоянным (неизменным) передаточным
4. По характеру изменения передаточного отношения (числа): передачи с постоянным (неизменным) передаточным

5. По подвижности осей и валов: с неподвижными осями валов − рядовые передачи (коробки скоростей, редукторы), передачи с подвижными осями валов (планетарные передачи, вариаторы с поворотными роликами).
6. По количеству ступеней преобразования движения: одно-, двух-, трех-, и многоступенчатые.
7. По конструктивному оформлению: закрытые и открытые (бескорпусные).
Слайд 5Главные характеристики передач (2 слайда):
мощности на входном и выходном валах - Pвх,
Главные характеристики передач (2 слайда):
мощности на входном и выходном валах - Pвх,

и их скорости вращения ωвх, ωвых или частоты вращения - nвх и nвых.
Соотношение между частотой вращения n (общепринятая размерность 1/мин) и угловой скоростью ω (размерность в системе SI 1/с) выражается следующим образом:
и (2.1)
Отношение мощности на выходном валу передачи Pвых (полезной мощности) к мощности Pвх, подведенной к входному валу (затраченной), называют коэффициентом полезного действия (КПД):
(2.2)
Отношение потерянной в механизме (машине) мощности (Pвх - Pвых) к ее входной мощности называют коэффициентом потерь:
(2.3)
Слайд 6Сумма коэффициентов полезного действия и потерь всегда равна единице:
(2.4)
Для многоступенчатой передачи, включающей
Сумма коэффициентов полезного действия и потерь всегда равна единице:
(2.4)
Для многоступенчатой передачи, включающей

. (2.5)
Следовательно КПД машины, содержащей ряд последовательных передач, всегда будет меньше КПД любой из этих передач.
Силовые показатели передачи определяются по известным из теории механизмов и машин (ТММ) формулам.
усилие, действующее по линии движения на поступательно движущейся детали F=P/v, где P − мощность, подведенная к этой детали, а v − ее скорость;
момент, действующий на каком-либо из валов передачи T=P/ω, где P − мощность, подведенная к этому валу, а ω − скорость его вращения. Используя соотношение (2.1), получаем формулу, связывающую момент, мощность и частоту вращения:
. (2.6)
Слайд 7Окружная (касательная) скорость в любой точке вращающегося элемента (колеса, шкива, вала), лежащей
Окружная (касательная) скорость в любой точке вращающегося элемента (колеса, шкива, вала), лежащей

. (2.7)
При этом тангенциальную (окружную или касательную) силу можно вычислить по следующей формуле:
. (2.8)
Передаточное отношение - это отношение скорости входного звена к скорости выходного звена, что для вращательного движения выразится следующим образом:
, (2.9)
где верхний знак (плюс) соответствует одинаковому направлению вращения входного и выходного звеньев (валов), а нижний - встречному.
Слайд 8В технических расчетах (особенно прочностных) направление вращения чаще всего не имеет решающего
В технических расчетах (особенно прочностных) направление вращения чаще всего не имеет решающего

. (2.10)
В многоступенчатой передаче с последовательным расположением k ступеней (что чаще всего наблюдается в технике) передаточное число и передаточное отношение определяются следующими выражениями:
. (2.11)
Среди множества разнообразных передач вращательного движения достаточно простыми конструктивно (по устройству) являются передачи с гибкой связью, принцип работы которых строится на использовании сил трения или зубчатого зацепления − это ременные передачи.
Слайд 9Определение:
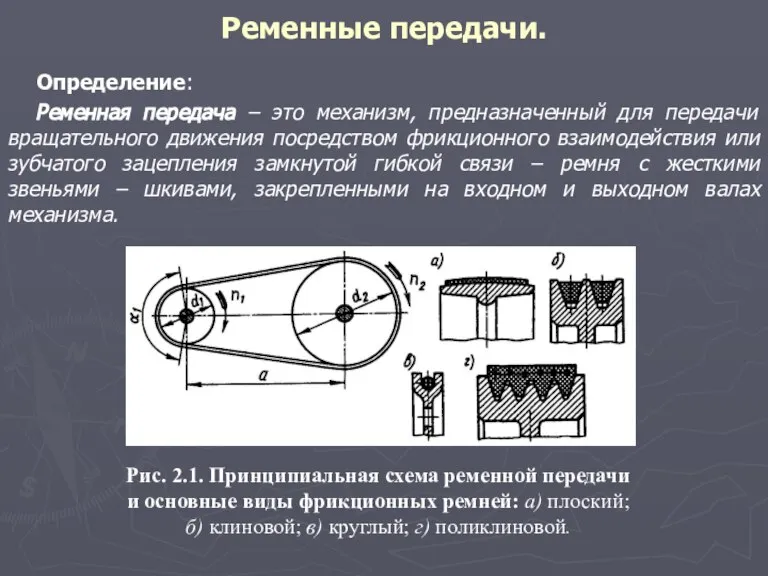
Ременная передача – это механизм, предназначенный для передачи вращательного движения посредством фрикционного
Определение:
Ременная передача – это механизм, предназначенный для передачи вращательного движения посредством фрикционного
Ременные передачи.
Слайд 10Достоинства ременных передач:
1. Простота конструкции и низкая стоимость.
2. Возможность передачи
Достоинства ременных передач:
1. Простота конструкции и низкая стоимость.
2. Возможность передачи

3. Возможность работы с большими скоростями вращения шкивов.
4. Плавность и малошумность работы.
5. Смягчение крутильных вибраций и толчков за счет упругой податливости ремня.
6. Предохранение механизмов от перегрузки за счет буксования ремня при чрезмерных нагрузках.
Недостатки ременных передач:
1. Относительно большие габариты.
2. Малая долговечность ремней.
3. Большие поперечные нагрузки, передаваемые на валы и их подшипники.
4. Непостоянство передаточного числа за счет проскальзывания ремня.
5. Высокая чувствительность передачи к попаданию жидкостей (воды, топлива, масла) на поверхности трения.
Слайд 11Классификация ременных передач (2 слайда):
1. По форме поперечного сечения ремня:
1.1 плоскоременные
Классификация ременных передач (2 слайда):
1. По форме поперечного сечения ремня:
1.1 плоскоременные

1.2 клиноременные (поперечное сечение ремня в форме трапеции рис. 2.1.б);
1.3 поликлиноременные (наружная поверхность ремня плоская, а внутренняя, взаимодействующая со шкивами, поверхность ремня снабжена продольными гребнями, в поперечном сечении имющими форму трапеции, рис. 2.1.г);
1.4 круглоременные (поперечное сечение ремня имеет форму круга, рис. 2.1.в);
1.5 зубчатоременная (внутренняя, контактирующая со шкивами, поверхность плоского ремня снабжена поперечными выступами, входящими в процессе работы передачи в соответствующие впадины шкивов).
2. По взаимному расположению валов и ремня:
2.1 открытая передача – передача с параллельными геометрическими осями валов и ремнем, охватывающим шкивы в одном направлении (шкивы вращаются в одном направлении);
2.2 перекрестная передача – передача с параллельными валами и ремнем, охватывающим шкивы в противоположных направлениях (шкивы вращаются во встречных направлениях);
2.3 полуперекрестная передача – оси валов которой перекрещиваются под некоторым углом (чаще всего 90°).
Слайд 123. По числу и виду шкивов, применяемых в передаче:
3.1 с одношкивными
3. По числу и виду шкивов, применяемых в передаче:
3.1 с одношкивными

3.2 с двушкивным валом, один из шкивов которого холостой;
3.3 с валами, несущими ступенчатые шкивы для изменения передаточного числа (для ступенчатой регулировки скорости ведомого вала).
4. По количеству валов, охватываемых одним ремнем:
двухвальная,
трех-,
четырех- и
многовальная передача.
5. По наличию вспомогательных роликов:
без вспомогательных роликов,
с натяжными роликами;
с направляющими роликами.
Слайд 13При расчетах клиноременных передач для ведущего и ведомого шкивов используются расчетные диаметры
При расчетах клиноременных передач для ведущего и ведомого шкивов используются расчетные диаметры

, (2.12)
Геометрические соотношения в ременной передаче рассмотрим на примере открытой плоскоременной передачи (рис. 2.2). Межосевое расстояние a – это расстояние между геометрическими осями валов, на которых установлены шкивы с диаметрами D1 (он, как правило, является ведущим) и D2 (ведомый шкив).
Рис. 2.2. Геометрия открытой
ременной передачи.
Слайд 14а так как этот угол обычно невелик, то во многих расчетах допустимым
а так как этот угол обычно невелик, то во многих расчетах допустимым

. (2.13)
Используя это допущение, угол охвата ремнем малого шкива можно представить в следующем виде
(2.14)
в радианной мере, или
(2.15)
в градусах.
Длину ремня при известных названных выше параметрах передачи можно подсчитать по формуле
. (2.16)
Однако, весьма часто ремни изготавливаются в виде замкнутого кольца известной (стандартной) длины. В этом случае возникает необходимость уточнять межосевое расстояние по заданной длине ремня
Слайд 15. (2.17)
С целью обеспечения стабильности работы передачи обычно принимают
для плоского ремня − ,
С целью обеспечения стабильности работы передачи обычно принимают
для плоского ремня − ,

а для клинового – ,
где hp – высота поперечного сечения ремня (толщина ремня).
В процессе работы передачи ремень обегает ведущий и ведомый шкивы. Долговечность ремня в заданных условиях его работы характеризует отношение Vp / Lp (в системе СИ его размерность– с-1), чем больше величина этого отношения, тем ниже при прочих равных условиях долговечность ремня. Обычно принимают
для плоских ремней − Vp / Lp = (3…5) с-1,
для клиновых − Vp / Lp = (20…30) с-1.
Слайд 16Силовые соотношения в ременной передаче. В ременной передаче силы нормального давления между
Силовые соотношения в ременной передаче. В ременной передаче силы нормального давления между

Рис. 2.3. Силы в ременной передаче.
передачи за счет трения ведущего шкива о ремень набегающая на этот шкив ветвь ремня получает дополнительное натяжение (сила F1), а, сбегающая с ведущего шкива, ветвь ремня несколько ослабляется (сила F2, рис. 2.3,б).
Окружное усилие, передающее рабочую нагрузку Ft = F1-F2, но, как для передачи вращения Ft = 2T2/D (см. (2.8)),
а для поступательно движущихся ветвей ремня Ft = P / Vp , где P – мощность передачи, а Vp − средняя скорость движения ремня. Суммарное натяжение ветвей ремня остается неизменным, как в работающей, так и в неработающей передаче, то есть F1+F2=2F0 .
Слайд 17Для ремня, охватывающего шкив, по формуле Эйлера F1=F2⋅ e f⋅α, где e
Для ремня, охватывающего шкив, по формуле Эйлера F1=F2⋅ e f⋅α, где e

, (2.19)
где индексы «1» указывают на параметры, относящиеся к ведущему шкиву передачи.
Отношение разности сил натяжения в ветвях ремня работающей передачи к сумме этих сил называется коэффициентом тяги (ϕ).
. (2.21)
Оптимальная величина коэффициента тяги:
. (2.22)
Оптимальная величина коэффициента тяги зависит только лишь от конструктивных параметров передачи и качества фрикционной пары материалов ремня и шкива.
Слайд 18Кинематика ременной передачи. Удлинение каждого отдельно взятого элемента ремня меняется в зависимости
Кинематика ременной передачи. Удлинение каждого отдельно взятого элемента ремня меняется в зависимости

1) работа ременной передачи без скольжения ремня по рабочей поверхности шкивов невозможна.;
2) скорости движения ведущей и свободной ветвей ремня различны, а следовательно, различны и скорости рабочих поверхностей ведущего и ведомого шкивов.
Окружная скорость рабочей поверхности ведущего шкива больше окружной скорости на поверхности ведомого шкива (V1 > V2).
Отношение разности между окружными скоростями на рабочей поверхности ведущего и ведомого шкивов к скорости ведущего шкива называют коэффициентом скольжения передачи (ξ).
, (2.23)
Слайд 19где индекс «1» соответствует ведущему, а индекс «2» − ведомому шкивам.
Передаточное число
где индекс «1» соответствует ведущему, а индекс «2» − ведомому шкивам.
Передаточное число

. (2.24)
Тяговая способность и долговечность ремня являются основными критериями работоспособности ременной передачи. Её проектный расчет обычно выполняется по тяговой способности, а расчет долговечности при этом является проверочным.
Рис. 2.4. Кривые скольжения и КПД.
Поведение ременной передачи характеризует график рис. 2.4. На нем выявляются 3 зоны:
1 зона упругого скольжения (0 ≤ ϕ ≤ ϕ0; ξ меняется линейно);
2 зона частичного буксования (ϕ0≤ϕ≤ϕmax, ξ быстро нарастает);
3 зона полного буксования (ϕ>ϕmax скольжение полное).
Слайд 20Напряжения в ремне. В ремне возникают напряжения от действия рабочей нагрузки, от
Напряжения в ремне. В ремне возникают напряжения от действия рабочей нагрузки, от

напряжения растяжения от рабочей нагрузки
; (2.25)
напряжения изгиба
; (2.26)
напряжения от действия центробежных сил
; (2.29)
где ρ − средняя плотность материала ремня, а Vр – средняя скорость движения ремня, обегающего шкив.
На внешней стороне ремня все три вида названных напряжений являются растягивающими и потому суммируются. Таким образом, максимальные растягивающие напряжения в ремне
. (2.31)
Слайд 21Особенности конструкции, работы и расчета клиноременных и поликлиноременных передач. Клиновые ремни имеют
Особенности конструкции, работы и расчета клиноременных и поликлиноременных передач. Клиновые ремни имеют
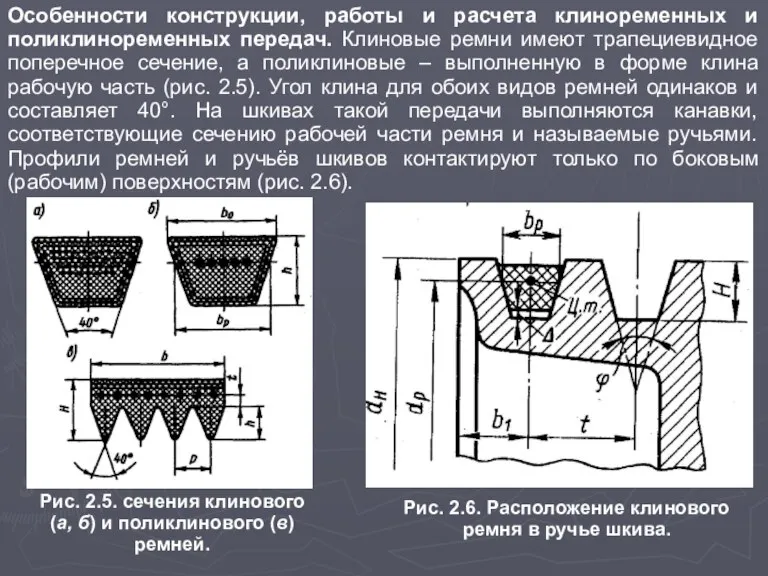
Рис. 2.6. Расположение клинового
ремня в ручье шкива.
Рис. 2.5. сечения клинового (а, б) и поликлинового (в) ремней.
Слайд 22Размеры сечений клиновых ремней стандартизованы (ГОСТ 1284.1-89, ГОСТ 1284.2-89, ГОСТ 1284.3-89). Стандартом
Размеры сечений клиновых ремней стандартизованы (ГОСТ 1284.1-89, ГОСТ 1284.2-89, ГОСТ 1284.3-89). Стандартом

Таким образом, ремень со шкивом образуют клиновую кинематическую пару, для которой приведенный коэффициент трения f* выражается зависимостью
, (2.36)
где f – коэффициент трения между контактирующими поверхностями ремня и шкива, а ϕ − угол между боковыми рабочими поверхностями ремня. При ϕ = 40° получаем, что f* = 2,92 f, то есть при одном и том же диаметре ведущего шкива несущая способность клиноременной передачи будет примерно втрое выше в сравнении с плоскоременной.
Проектный расчет клиноременных передач выполняется достаточно просто методом подбора, поскольку в стандартах указывается мощность, передаваемая одним ремнем при определенном расчетном диаметре меньшего шкива и известной средней скорости ремня или частоте вращения шкива.
 Стандарт cXML в корпоративных приложениях электронной коммерции
Стандарт cXML в корпоративных приложениях электронной коммерции Натюрморт в фотографии
Натюрморт в фотографии Золотой век русской культуры. Литература. Живопись
Золотой век русской культуры. Литература. Живопись титул констатирующего
титул констатирующего Повесть о настоящем человеке
Повесть о настоящем человеке Выпускающая кафедра«Механика механизмов и машин» Заведующий кафедрой Шевченко Игорь Владимирович
Выпускающая кафедра«Механика механизмов и машин» Заведующий кафедрой Шевченко Игорь Владимирович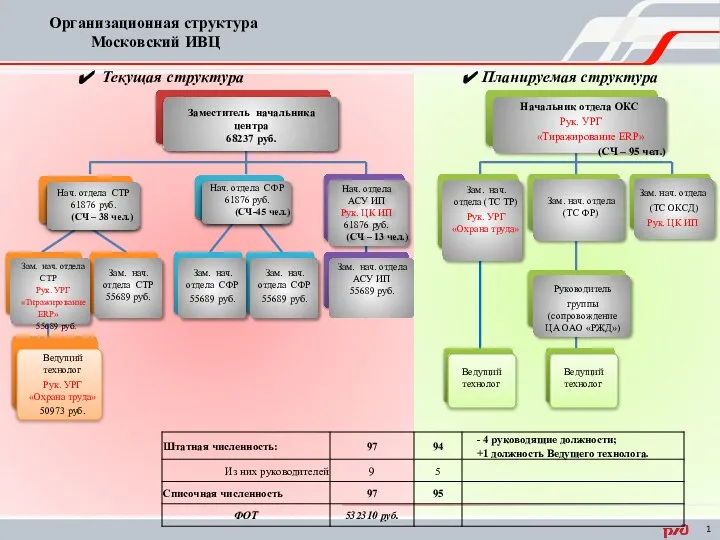 Организационная структура Московский ИВЦ
Организационная структура Московский ИВЦ День рождения Деда Мороза
День рождения Деда Мороза Поздравление с Новым годом
Поздравление с Новым годом Радиотехнические системы (РТС)
Радиотехнические системы (РТС) Презентация Microsoft PowerPoint [Автосохраненный]
Презентация Microsoft PowerPoint [Автосохраненный] Плюсы группы Т Плюс
Плюсы группы Т Плюс КВН – игра «В стране географов и географинь»
КВН – игра «В стране географов и географинь» Компьютерный кружок
Компьютерный кружок Изучение работы сварного соединения
Изучение работы сварного соединения  Осень… На улице холодно и сыро
Осень… На улице холодно и сыро Презентация на тему Познавательные способности
Презентация на тему Познавательные способности Башкирский государственный университет. Магистратура по социологии
Башкирский государственный университет. Магистратура по социологии Слово и время
Слово и время ИСПОЛЬЗОВАНИЕ МОБИЛЬНОГО КОМПЬЮТЕРНОГО КЛАССАВ УЧЕБНО-ВОСПИТАТЕЛЬНОМ ПРОЦЕССЕ МОУ СОШ 30
ИСПОЛЬЗОВАНИЕ МОБИЛЬНОГО КОМПЬЮТЕРНОГО КЛАССАВ УЧЕБНО-ВОСПИТАТЕЛЬНОМ ПРОЦЕССЕ МОУ СОШ 30 Презентация на тему Презентация "Буквы Уу Ээ"
Презентация на тему Презентация "Буквы Уу Ээ" Nature’s Sunshine Products
Nature’s Sunshine Products Православная молитва
Православная молитва ПСИХОЛОГИЧЕСКИЙ ВЕСТНИК
ПСИХОЛОГИЧЕСКИЙ ВЕСТНИК ИТОГИ РАБОТЫ ЗА 2011 ГОД
ИТОГИ РАБОТЫ ЗА 2011 ГОД Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании Северодвинск
Об утверждении положения о порядке реализации правотворческой инициативы граждан в муниципальном образовании Северодвинск Орнамент
Орнамент Презентация на тему А нужен ли Калгон?
Презентация на тему А нужен ли Калгон?