Решение задач с помощью графов

Граф
Простейшая модель системы.Отображает элементарный состав системы и структуру связей
Сеть
Граф с возможностью множества различных путей перемещения по ребрам между некоторыми парами вершин
Граф называется связным
если любая пара его вершин — связная.
Ребро соединяет две вершины графа
элемент (точка) графа, обозначающий объект любой природы, входящий в множество объектов, описываемое графом
Вершина
Ребро
это ориентированное ребро.
Дуга
ребро, начало и конец которого находятся в одной и той же вершине
Петля
любой связный граф, не имеющий циклов.
Дерево

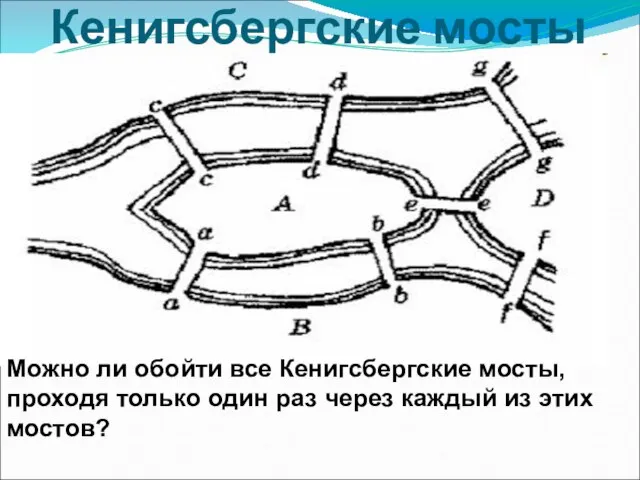
Кенигсбергские
мосты

Кенигсбергские мосты
Можно ли обойти все Кенигсбергские мосты, проходя только один раз через каждый из этих мостов?

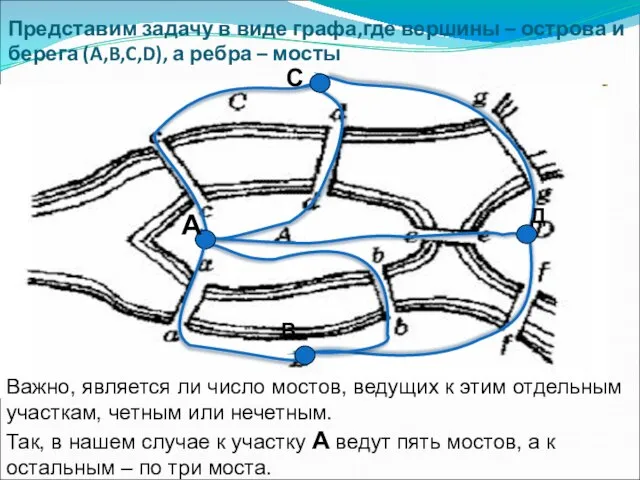
Представим задачу в виде графа,где вершины – острова и берега (A,B,C,D), а ребра – мосты
Важно, является ли число мостов, ведущих к этим отдельным участкам, четным или нечетным.
Так, в нашем случае к участку A ведут пять мостов, а к остальным – по три моста.

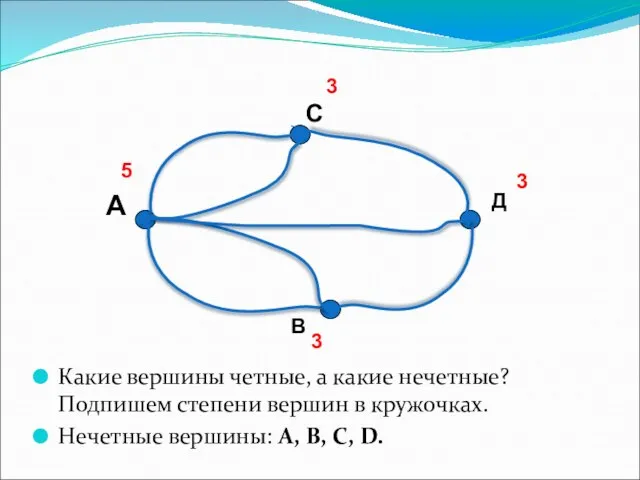
Какие вершины четные, а какие нечетные? Подпишем степени вершин в кружочках.
Нечетные вершины: А, B, C, D.
3
3
3
5

Если граф имеет цикл, содержащий все ребра графа по одному разу (Эйлерова линия),то такой граф называется эйлеровым графом
Условия существования Эйлеровой линии:
-граф связный
-все вершины четные
Другими словами, эйлеров граф – это граф,который можно нарисовать одним росчерком
Эйлеров граф

Алгоритм решения задач
1. Нарисовать граф, где вершины – острова и берега, а ребра – мосты.
2. Определить степень каждой вершины и подписать возле нее.
3. Посчитать количество нечетных вершин.
4. Обход возможен:
a. ЕСЛИ все вершины – четные, и его можно начать с любого участка.
b. ЕСЛИ 2 вершины – нечетные, но его нужно начать с одной из нечетных местностей.
5. Обход невозможен, если нечетных вершин больше 2.
6. Сделать ВЫВОД.
7. Указать Начало и Конец пути.

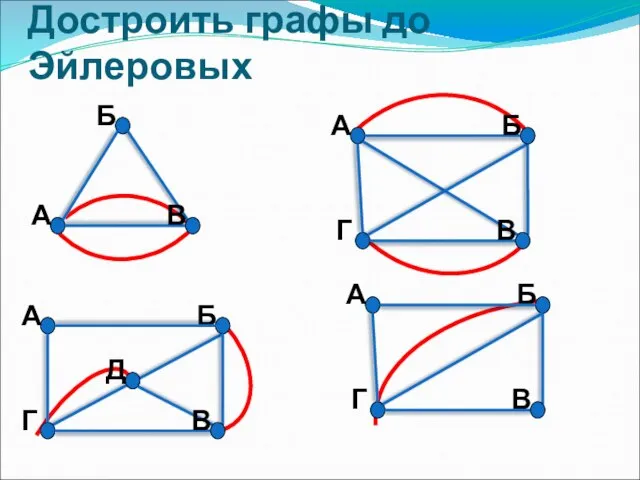
Достроить графы до Эйлеровых

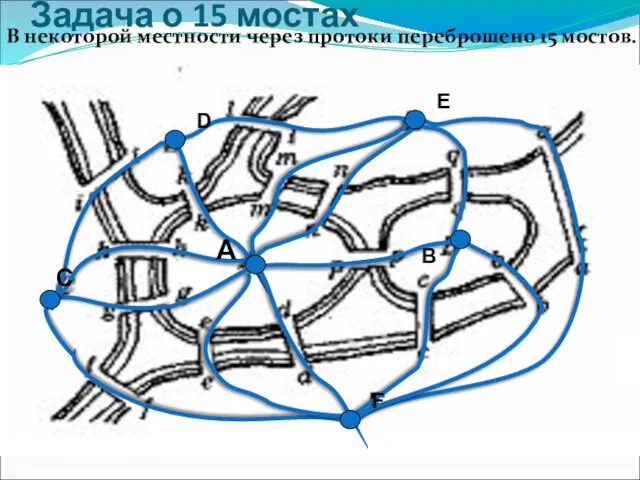
Задача о 15 мостах
В некоторой местности через протоки переброшено 15 мостов.