СУПЕРЭЛИТНЫЕ ПЛАЗМЕННЫЕ КОЛЬЦА И ОРБИТЫ ПЛАНЕТ И СПУТНИКОВ, ИЗОМОРФНЫЕ ОРБИТАМ ЭЛЕКТРОНОВ В ВОДОРОДОПОДОБНЫХ АТОМАХ

Аннотация
Рассматривается проблема квантования секториальных скоростей, радиусов и периодов вращения элементов кольца, состоящего из холодной плазмы с высокой электронной концентрацией, плотность которой убывает в радиальном направлении, вращающегося в гравитационно-магнитном поле центрального тела. Вводится понятие суперэлитных колец, изоморфных с орбитами планет Солнечной системы и их спутников. Доказывается изоморфизм последних по отношению к орбитам электронов в водородоподобных атомах. Предварительные результаты см. в [8-12].

Super elite plasma rings and planets’ and moons’ orbits isomorphous to the electrons orbits in hydrogen-like atoms
The present study is continuation and generalization of some previous results obtained for the plasma ring having constant density, rotating in the gravity-magnetic field of the central body. The object under consideration is a ring with the density decreasing in radial direction. The quantization problem is examined for the sectarian and orbital velocities and for the periods of the elite plasma rings rotation. We introduce a new conception of super elite rings isomorphous relative to the orbits of the planets and moons in the Sun system. We demonstrate isomorphism of these orbits relative to the electron orbits in the hydrogen-like atoms.

ИЗОМОРФИЗМ СОЛНЕЧНОЙ СИСТЕМЫ И
ВОДОРОДОПОДОБНЫХ АТОМОВ

Изоморфные характеристики объектов Солнечной системы и атома водорода [3]

Характеристики планет солнечной системы.
Земная группа [3]

Характеристики планет солнечной системы.
Юпитерианская группа [3]

Квантовые числа (N) спутников Урана (N mu) и Нептуна (N mn), открытых КА Voyager-2 [4, 5]

Зависимость удвоенной секториальной скорости, нормированной к ее кванту, от квантового числа N [3]

Принцип Четаева-Молчанова
Устойчивые планетарные и спутниковые системы, подобные соответствующим элементам Солнечной системы, обладают следующими свойствами:
Орбиты планет и спутников квантуются.
Соответствующие подсистемы близки к резонансным, то есть их движение является периодическим или очень близким к нему.

ПЛАНЕТНЫЕ КОЛЬЦА КАК РЕЛИКТЫ ПЛАЗМЕННЫХ ПРАКОЛЕЦ

Диск вокруг молодой звезды
AU MicroscopII

Кольца Сатурна: общая картина;
кольца B, C; A

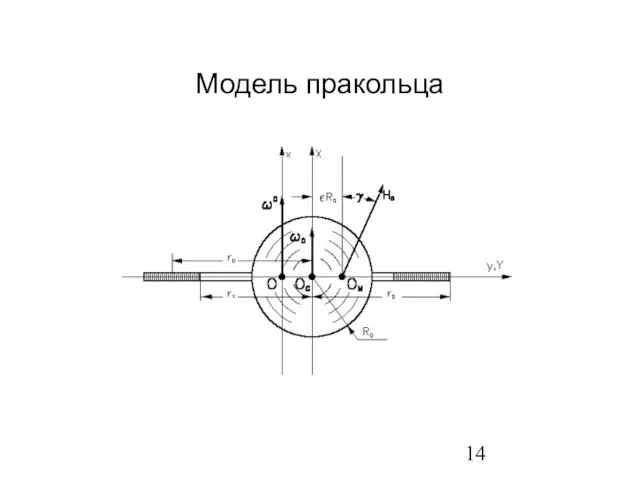
Модель пракольца

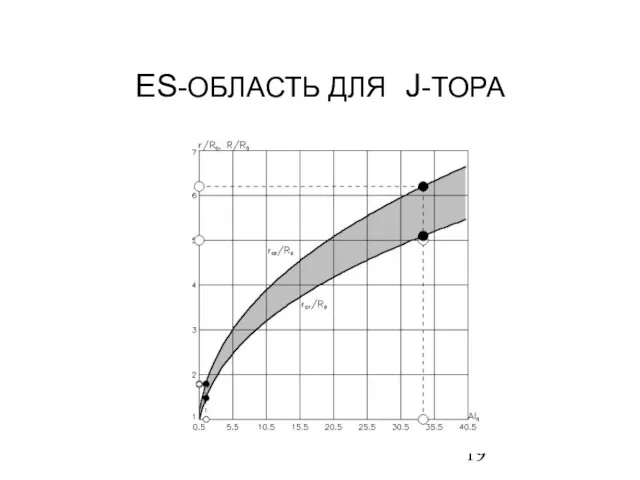
Уравнения границ ES-области
Al0 > (1/3)1/2; r01/R0 < r0/R0 < r02/R0;
r01/R0 = 31/5 Al02/5; r02/R0 = 81/5 Al02/5;
Al0 = a0/VG0 ; a0 = H0(µ0/ρ)1/2. (1)

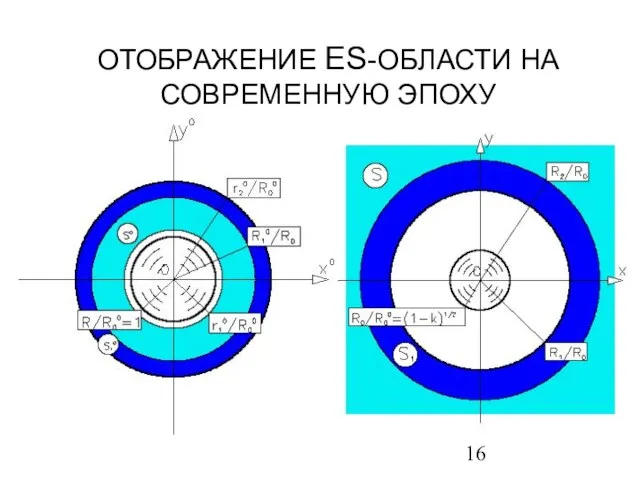
ОТОБРАЖЕНИЕ ES-ОБЛАСТИ НА СОВРЕМЕННУЮ ЭПОХУ

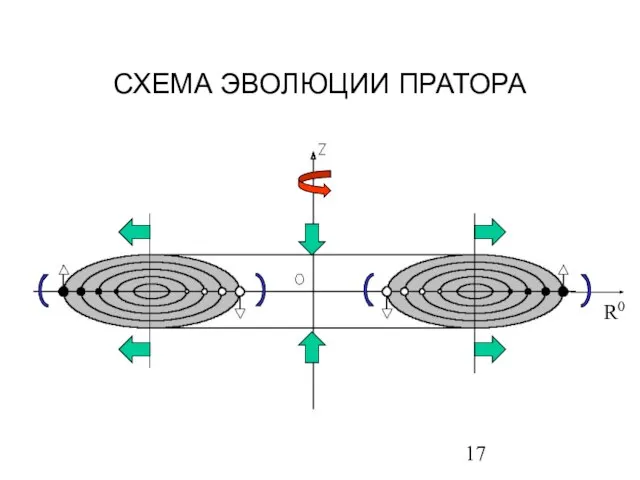
СХЕМА ЭВОЛЮЦИИ ПРАТОРА
R0

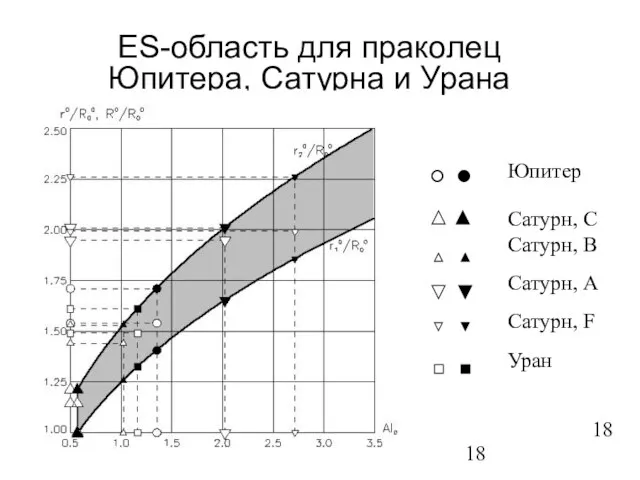
ES-область для праколец Юпитера, Сатурна и Урана
Сатурн, С
Сатурн, B
Сатурн, A
Сатурн, F
Уран
Юпитер

ES-ОБЛАСТЬ ДЛЯ J-ТОРА

ПАРАМЕТР Ω И ПЛОТНОСТЬ ПЛАЗМЫ
γΩ= (VM r0/R0)/(ar0/ R0);
ar0/R0 = const = a0, VM >> ω0 r0;
a = a0 (R0 /r0)3 (ρ/ρ0)-1/2. (2)
ρ/ρ0 = (R0 /r0)4, a = a0 R0 /r0,
(γΩ)2 = (VM r0)2/(a0R0)2 =
= (VG0 /a0)2(r0/R0) – 3. (3)

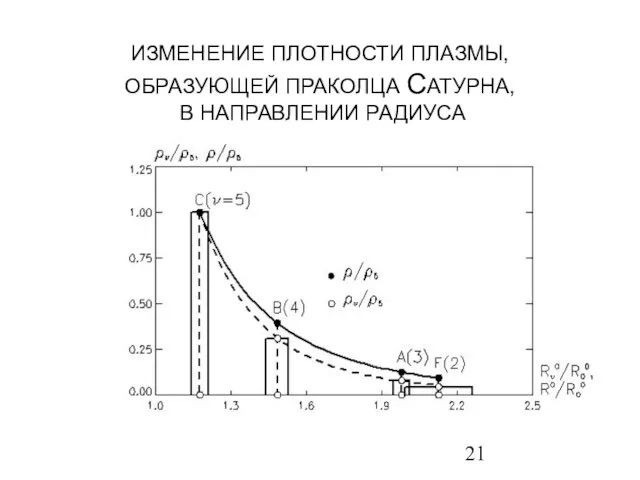
ИЗМЕНЕНИЕ ПЛОТНОСТИ ПЛАЗМЫ, ОБРАЗУЮЩЕЙ ПРАКОЛЦА САТУРНА,
В НАПРАВЛЕНИИ РАДИУСА

ПАРАМЕТР Ω И ЕГО ЭЛИТНЫЕ СОБСТВЕННЫЕ ЗНАЧЕНИЯ

РАЗРЕШАЮЩЕЕ УРАВНЕНИЕ
zk+2 - 2 chα zk+1 + zk = 0; (4) k = 0, 1, 2, …, K – 1; K = N/2;
z0 = 0; zK+1 = 0.
k = (μ – 1)/2; m = μ +1 – ν; μ>>1;
p = i(μ +1- ν)Ω = i[2(k +1) -ν]Ω,
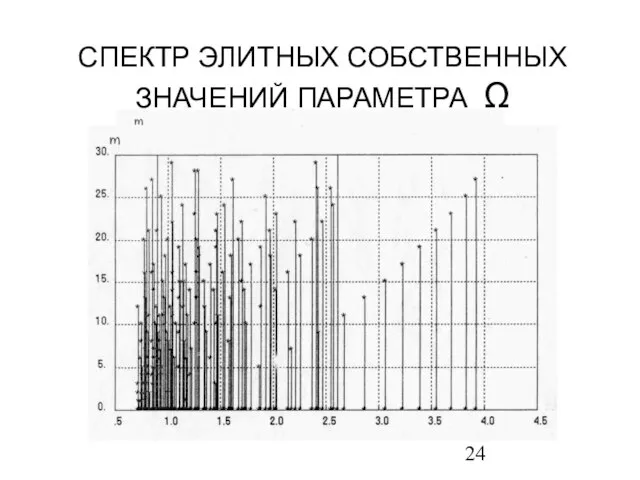
2chα = 2[1 -νΩ2/(k+1)]. (5)

СПЕКТР ЭЛИТНЫХ СОБСТВЕННЫХ ЗНАЧЕНИЙ ПАРАМЕТРА Ω
a)
a)

АНАЛИТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ Ω
Ωνs = ((Κ+1)/ν)1/2 sin (πs)/(2(Κ+1)); (6)
s = Κ − ν + 1, Κ−ν, Κ−ν−1, …, 1;
k = s + ν - 2; ν = 1, 2,…, Κ; Κ = Ν/2.
Ωnλj = (n/ν)1/2 sin (jπ)/(2n); (8)
j = ± λ; λ = K - ν + 1/2; n = K+ 1; ν = 1, 2, …, K
Ωνkn = (n/ν)1/2 sin (πk)/2n; (7)
k = 0, ± l; l = K+1-ν; n = K + 1; ν = 1, 2, …, K.

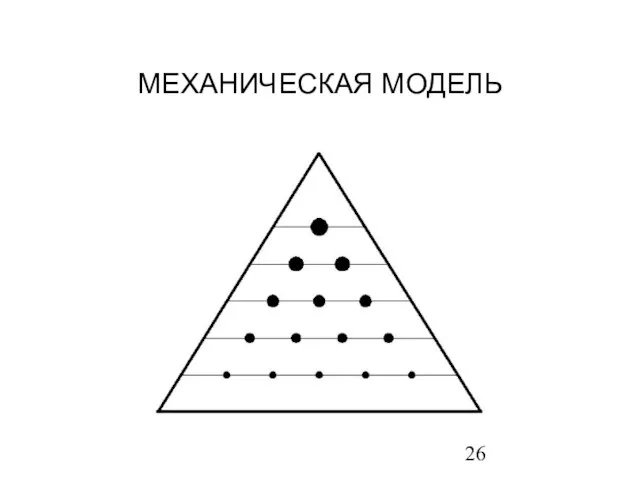
МЕХАНИЧЕСКАЯ МОДЕЛЬ

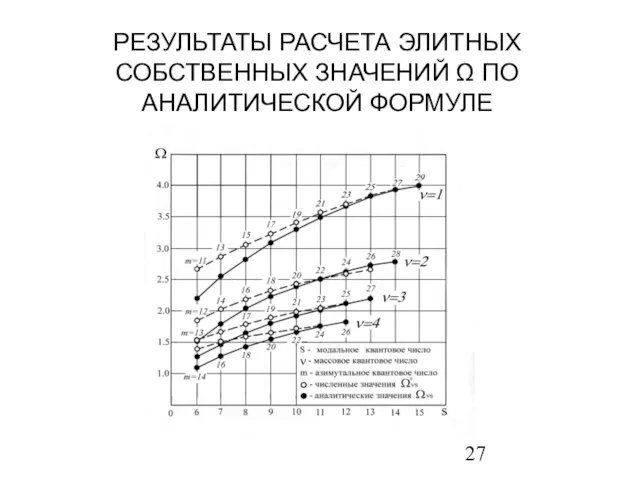
РЕЗУЛЬТАТЫ РАСЧЕТА ЭЛИТНЫХ СОБСТВЕННЫХ ЗНАЧЕНИЙ Ω ПО АНАЛИТИЧЕСКОЙ ФОРМУЛЕ

СМЕЖНЫЕ ЭЛИТНЫЕ ВИХРЕВЫЕ КОЛЬЦА. ДОМИНАНТНАЯ МОДА

Принцип элитных колец
Плазменное кольцо, вращающееся в гравитационно-магнитном поле, эволюционирует к системе дискретных элитных колец со средними радиусами, соответствующими элитным собственным значениям параметра Ω. Эти кольца характеризуются наличием долго живущих стационарных возмущений. Эволюционно зрелое плазменное кольцо представляет собой систему элитных колец, разделенных антикольцами, т.е. щелями. Радиусы средних линий первых объектов соответствуют целым квантовым числам n, l, m*, а вторых – целому квантовому числу n и полуцелым квантовым числам λ и j

СУПЕРЭЛИТНЫЕ КОЛЬЦА

ПРЕОБРАЗОВАНИЕ РАДИУСОВ ЭЛИТНЫХ КОЛЕЦ
(9)
(10)

Квантовые числа N и суперэлитные кольца
γΩν = ν – ½; ν = νPM, νPM + 1,…, νmax << [γ – 2] (11)
N2 = ν;
κ =1/9; N = NPM, NPM +1, …, N max <<γ -1.
(12)

ИЗОМОРФНЫЕ ПАРАМЕТРЫ СОЛНЕЧНОЙ СИСТЕМЫ И АТОМА ВОДОРОДА

Критерий Блехмана [6]
Необходимым условием устойчивости системы отвечают такие начальные положения взаимодействующих тел, движущихся вокруг центрального тела по кеплеровым орбитам, при котором средняя потенциальная энергия системы является минимальной.

Критерий Блехмана (продолжение)
В случае круговой орбиты N+1-го тела и эллиптической орбиты N-го тела устойчивости системы соответствует соединение при прохождении внутренним телом своего перицентра.
В случае эллиптической орбиты N+1-го тела и круговой орбиты N-го тела устойчивости системы соответствует противостояние при прохождении внешним телом своего апоцентра

ЗАКЛЮЧЕНИЕ

Сценарий эволюции пракольца
Элитные кольца, возникающие на начальной стадии эволюции плазменного пракольца.
Суперэлитные кольца, из которых формируются вследствие гравитационной неустойчивости будущие планеты или спутники.

Сценарий эволюции пракольца (продолжение)
3. Отсутствие фазовой дестабилизации каждого из этих объектов гравитационными возмущениями со стороны всех остальных (необходимое условие устойчивости ).
4. Амплитудно - фазовая стабилизация каждого из этих объектов гравитационными возмущениями со стороны всех остальных (достаточное условие устойчивости).

Основные выводы
Благодаря учету магнитогидродинамических эффектов в эпоху предыстории праоблака удалось получить на основе асимптотического решения краевой задачи механики сплошных сред квантование орбит в возникших из него в ходе эволюции планетарных и спутниковых системах, то есть доказать первый пункт сформулированного принципа Четаева-Молчанова. В то же время второй пункт этого принципа продолжает пока носить эвристический характер.

Слова Макса Планка о кванте действия
«…Когда я оглядываюсь на времена двадцатилетней давности, времена, когда впервые из опытных фактов начали вырисовываться понятия и величины физического кванта действия, и на долгий и извилистый путь, приведший в конце концов к его открытию, то все это кажется мне теперь иллюстрацией к давно доказанным словам Гете, что человек заблуждается покуда у него есть стремления. И вся напряженная работа духа могла бы показаться прилежному исследователю тщетной и безнадежной, если бы иногда поразительные факты не давали ему в руки неопровержимые доказательства того, что он в конце своего тернистого пути , по крайней мере, хоть на шаг приблизился к истине…»
Из Нобелевской лекции, 1920 г.

Благодарности
Автор благодарен
Владимиру Игоревичу Арнольду,
представившему к публикации первую версию работы,
Равилю Равильевичу Назирову
за постоянное внимание и поддержку,
Михаилу Яковлевичу Марову
за благожелательное обсуждение концептуального базиса работы,
Виктории Прохоренко
за творческое участие в подготовке доклада
Благодарности

Литература
Четаев Н.Г. Об устойчивых траекториях динамики. В сб. Устойчивость движения. Работы по аналитической механике. М.: Изд. АН СССР, 1962. С. 255.
Молчанов А.М. О резонансной структуре Солнечной системы. // Современные проблемы небесной механики и астродинамики. М.: Наука. Главная редакция физ. мат. литературы, 1973.
Гареев Ф.А. Геометрическое квантование микро- и макросистем. Планетарно-волновая структура адронных резонансов // Сообщения Объединенного Института Ядерных Исследований. Дубна, 1996. Р. 296-456.
Чечельницкий А.М. Система Урана. Солнечная система и волновая астродинамика. Прогноз теории и наблюдения КА "Вояджер 2" // ДАН СССР, 1988. Т. 303. № 5. С. 1082-1088.
Chechelnitsky A.M. Neptune – unexpected and predicted. Prognosis of theory and Voyager 2 observations // Report (IAF-92-0009) to the World Space Congress. Washington, DC. AIAA Prepr., 1992.
Блехман И.И. Синхронизация в природе и в технике. М.: Наука. Главная редакция физ. мат. литературы, 1981.