Содержание
- 2. Проблема исследования: Показать исторические истоки теоремы, умение применять полученные знания к решению прикладных задач.
- 3. Цель исследования: Обобщить и систематизировать знания по теме, учиться воспринимать материал в целостной системе различных предметов.
- 4. Задачи исследования: Расширение познавательного интереса к изучению геометрии. Разносторонний подход к изучению данной темы: как историки,
- 5. теорема В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- 6. Интересные факты Память . Афоризмы. Высказывания. Разное.
- 7. Память. Памятник Пифагору находится в порту города Пифагория и напоминает всем о теореме Пифагора, наиболее известном
- 8. Афоризмы. «Не садись на хлебную меру» С равным достоинством относись к малым и великим мира сего.
- 9. Изречения Пифагора Статуя формой своей хороша, А человека украсят дела. Шуткой беседу укрась, освети. Шутка, что
- 10. Разное. Пифагор первым определил и изучил взаимосвязь музыки и математики. Пифагор рассматривал геометрию не как практическую
- 11. Не алгебраические доказательства теоремы: Простейшее доказательство. Древнекитайское доказательство. Древнеиндийское доказательство. Доказательство Евклида.
- 12. . "Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах." Простейшее доказательство
- 13. Древнекитайское доказательство. Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело
- 14. . Древнеиндийское доказательство. Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть
- 15. . Доказательство Евклида приведено в предложении 47 первой книги «Начал». На гипотенузе и катетах прямоугольного треугольника
- 16. Лирики о теореме Пифагора . теореме Пифагора посвятил свои стихи немецкий писатель А.Шамиссо Прибудет вечной истина,
- 17. Задачи по планиметрии с практическим применением 12 апреля 1961 года Ю.А. Гагарин на космическом корабле “Восток”
- 18. . От пристани одновременно отплыли два корабля:один на юг, со скоростью 16 морских миль в час,
- 19. . «ИСТОРИЧЕСКИЕ ЗАДАЧИ» Задача индийского математика XII века Бхаскары . «На берегу реки рос тополь одинокий.
- 20. Задача из китайской «Математики в девяти книгах» . «Имеется водоем со стороной в 1 чжан =
- 21. Задача из учебника «Арифметика» Леонтия Магницкого . «Случися некому человеку к стене лестницу прибрати, стены же
- 22. . . Суть истины вся в том, что нам она – навечно, Когда хоть раз в
- 24. Скачать презентацию





















 Кто такой предприниматель?
Кто такой предприниматель? Кишечная непроходимость
Кишечная непроходимость  Гражданство и дееспособность
Гражданство и дееспособность QRPp
QRPp Особенности ФСКП
Особенности ФСКП Планирование, как функция менеджмента
Планирование, как функция менеджмента  Презентация на тему Миграции населения России (8 класс)
Презентация на тему Миграции населения России (8 класс) Презентация на тему Памятники Минска (виртуальной экскурсии по столице Белоруссии)
Презентация на тему Памятники Минска (виртуальной экскурсии по столице Белоруссии) ОРДЕНОНОСЦЫр.п. Мулловка
ОРДЕНОНОСЦЫр.п. Мулловка Диагностика температурного режима музейных помещений при помощи тепловизионной техники
Диагностика температурного режима музейных помещений при помощи тепловизионной техники Пять шагов навстречу блогерам
Пять шагов навстречу блогерам Основы теории государства и права
Основы теории государства и права School of our dreams
School of our dreams День Конституции Российской Федерации. 5 класс
День Конституции Российской Федерации. 5 класс Цель песнопения в церкви и жизни
Цель песнопения в церкви и жизни Презентация на тему Религиозные ритуалы обычаи и обряды (4 класс)
Презентация на тему Религиозные ритуалы обычаи и обряды (4 класс) Фалсафа 6
Фалсафа 6 Презентация на тему Архитектура Древней Греции
Презентация на тему Архитектура Древней Греции  «ПРИМЕНЕНИЕ ТЕХНОЛОГИИ РАЗВИТИЯ ЦЕЛОСТНОГО МЫШЛЕНИЯ НА УРОКАХ РУССКОГО ЯЗЫКА И МАТЕМАТИКИ С ДЕТЬМИ ЗПР»
«ПРИМЕНЕНИЕ ТЕХНОЛОГИИ РАЗВИТИЯ ЦЕЛОСТНОГО МЫШЛЕНИЯ НА УРОКАХ РУССКОГО ЯЗЫКА И МАТЕМАТИКИ С ДЕТЬМИ ЗПР» Электрические сети
Электрические сети Деноминации в протестантской церкви
Деноминации в протестантской церкви MFWF Episode 3 Lesson 2A
MFWF Episode 3 Lesson 2A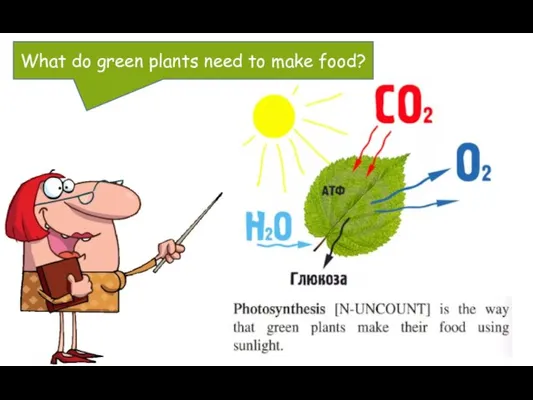 What do green plants need to make food?
What do green plants need to make food? Содержание сквозного курса информатики 7-11 класс
Содержание сквозного курса информатики 7-11 класс Urok_11_PR3_Kompyuternoe_predstavlenie_chisel
Urok_11_PR3_Kompyuternoe_predstavlenie_chisel Эффективный сайт для бизнеса, каким он должен быть?
Эффективный сайт для бизнеса, каким он должен быть? Группа компаний «МАГНОЛИЯ»
Группа компаний «МАГНОЛИЯ» Акробатические элементы. Упражнения на гибкость, растяжка, координация
Акробатические элементы. Упражнения на гибкость, растяжка, координация