Тесты ЕГЭ в PowerPoint

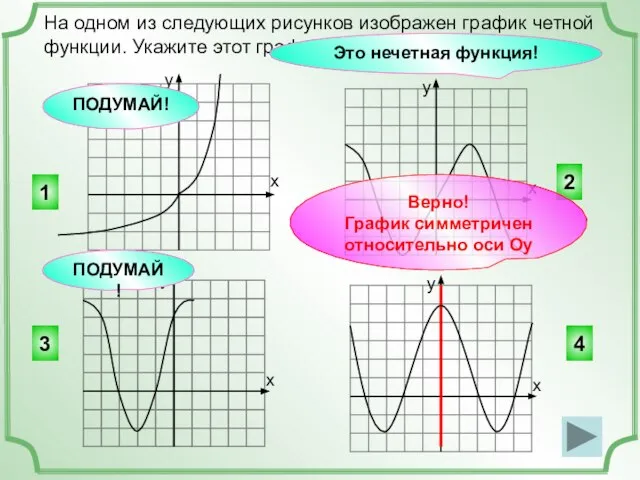
2
На одном из следующих рисунков изображен график четной функции. Укажите этот график.
х
у
х
у
х
у
х
у
Это нечетная функция!
Верно!
График симметричен относительно оси Оу
ПОДУМАЙ!
1
ПОДУМАЙ!
4
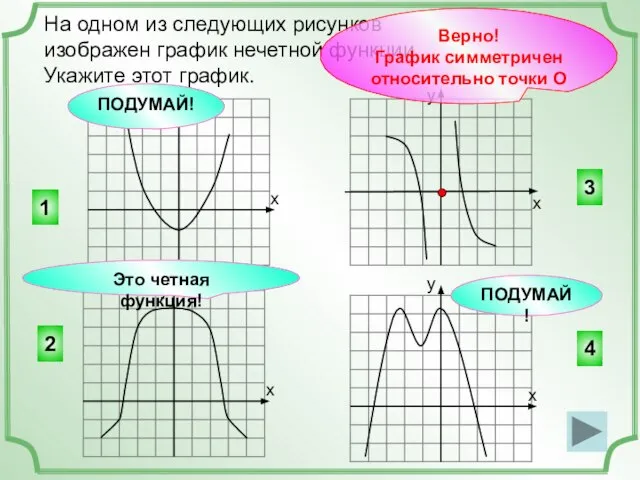
3

На одном из следующих рисунков
изображен график нечетной функции.
Укажите этот график.
3
4
2
1
ПОДУМАЙ!
у
х
х
х
х
у
у
Это четная функция!
у
ПОДУМАЙ!
Верно!
График симметричен относительно точки О

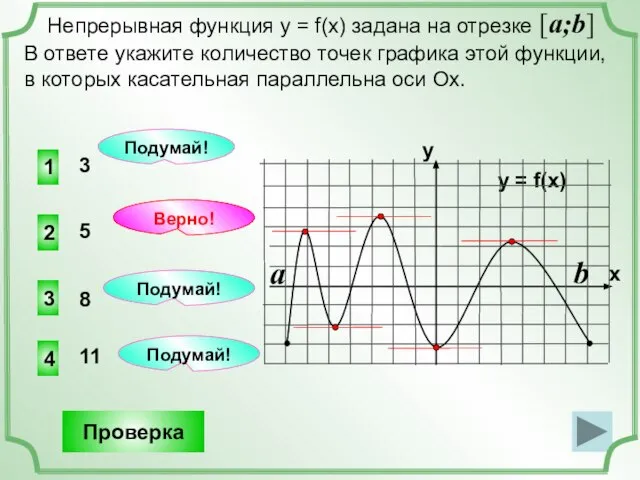
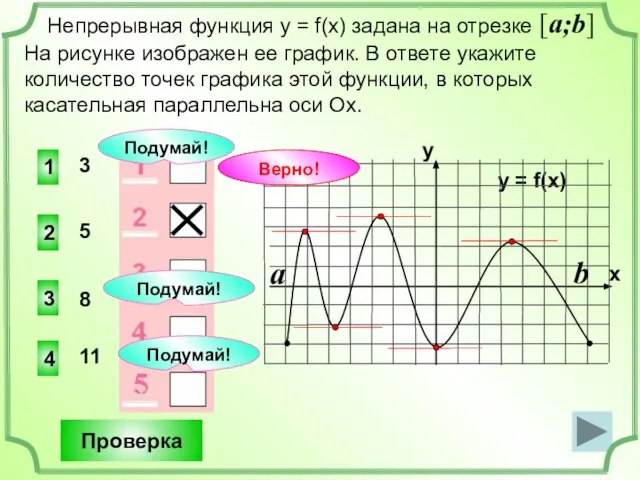
1
4
3
3
Непрерывная функция у = f(x) задана на отрезке [a;b]
В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.
Проверка
y = f(x)
y
x
2
11
8
Подумай!
Подумай!
Подумай!
Верно!
5
a
b

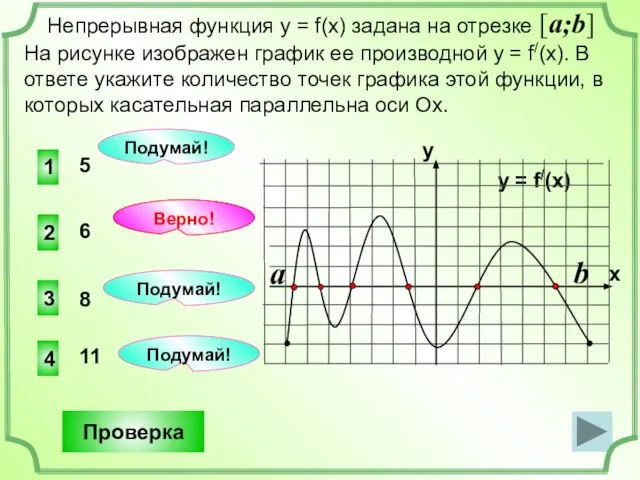
1
4
3
5
Непрерывная функция у = f(x) задана на отрезке [a;b]
На рисунке изображен график ее производной у = f/(x). В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.
Проверка
y = f/(x)
y
x
2
11
8
Подумай!
Подумай!
Подумай!
Верно!
6
a
b

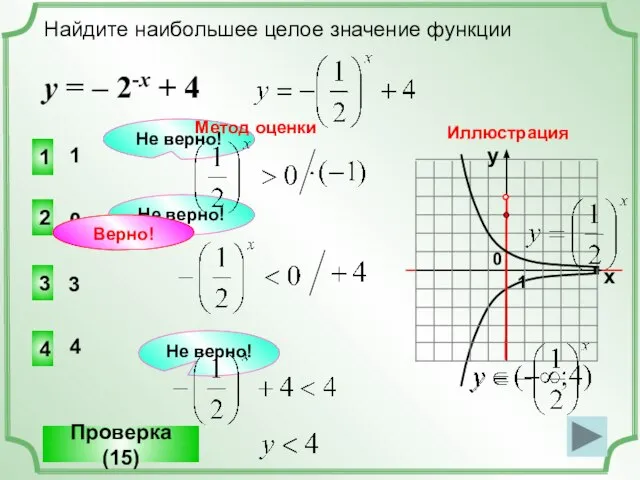
Найдите наибольшее целое значение функции
у = – 2-x + 4
3
2
4
1
Не верно!
Не верно!
Не верно!
Проверка (15)
0
1
4
3
Верно!
Метод оценки
Иллюстрация

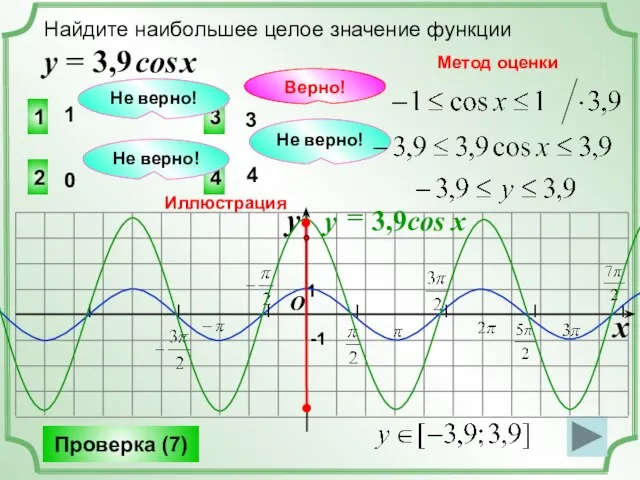
Найдите наибольшее целое значение функции
у = 3,9 cos x
3
2
4
1
Не верно!
Не верно!
Не верно!
Проверка (7)
0
1
4
3
Верно!
Метод оценки

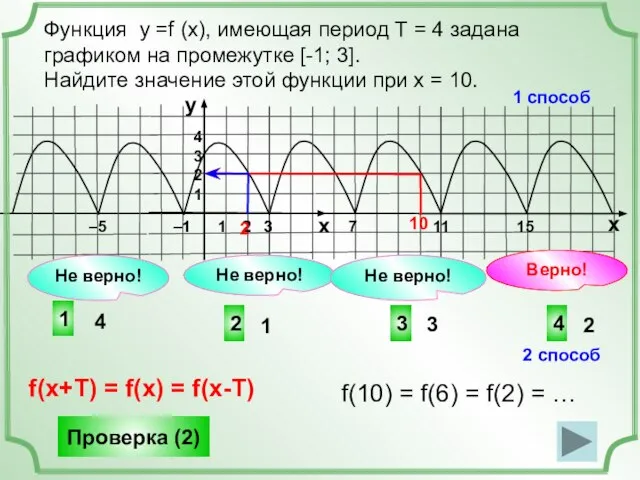
Функция у =f (x), имеющая период Т = 4 задана графиком на промежутке [-1; 3].
Найдите значение этой функции при х = 10.
4
3
1
2
4
1
3
2
Проверка (2)
4
3
2
1
y
–1 1 2 3
Не верно!
Не верно!
Не верно!
Верно!
f(x+Т) = f(x) = f(x-T)
f(10) = f(6) = f(2) = …
1 способ
2 способ
10
2

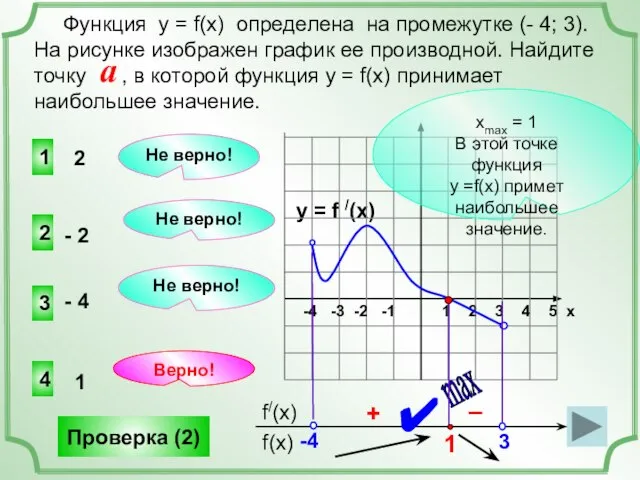
y = f /(x)
1 2 3 4 5 х
-4 -3 -2 -1
4
3
1
2
Не верно!
Не верно!
Не верно!
2
- 2
- 4
1
Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. Найдите точку , в которой функция у = f(x) принимает наибольшее значение.
+
a
Верно!
Проверка (2)
хmax = 1
В этой точке функция
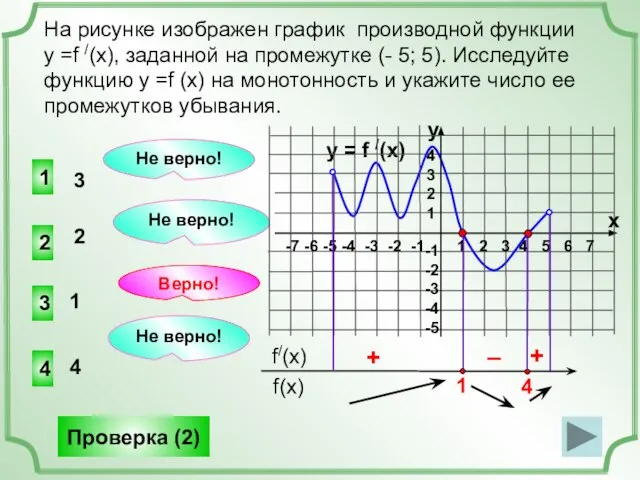
у =f(x) примет наибольшее значение.
–

На рисунке изображен график производной функции
у =f /(x), заданной на промежутке (- 5; 5). Исследуйте функцию у =f (x) на монотонность и укажите число ее промежутков убывания.
3
2
4
1
Не верно!
Не верно!
Верно!
Не верно!
3
2
1
4
Проверка (2)
+
–
y = f /(x)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
+

y = f /(x)
1
3
4
2
Не верно!
Не верно!
Не верно!
8
6
4
9
Функция у = f(x) определена на промежутке на промежутке (- 6; 3). На рисунке изображен график ее производной. Найдите длину промежутка убывания этой функции.
+
–
Верно!
Проверка (2)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
y
x

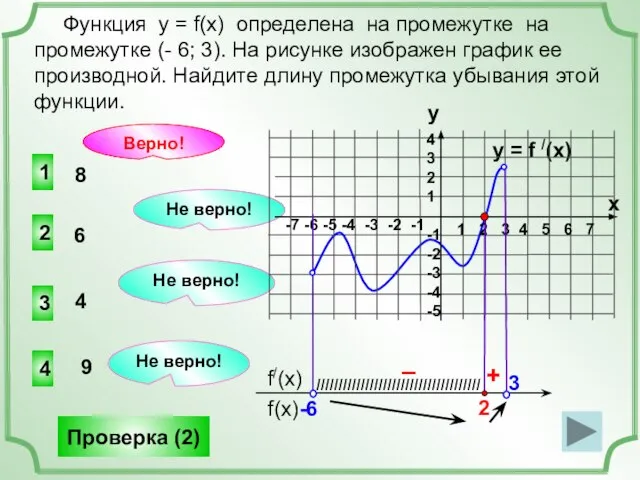
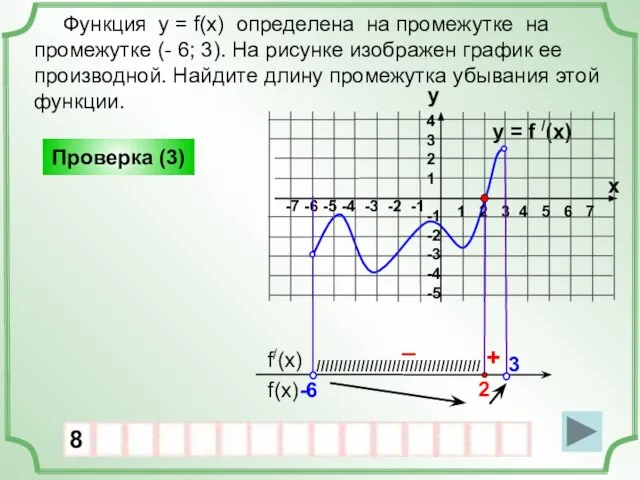
y = f /(x)
Функция у = f(x) определена на промежутке на промежутке (- 6; 3). На рисунке изображен график ее производной. Найдите длину промежутка убывания этой функции.
+
–
Проверка (3)
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
y
x
8

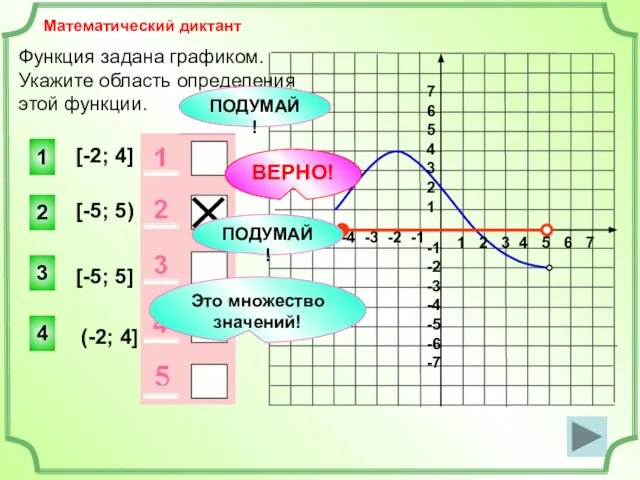
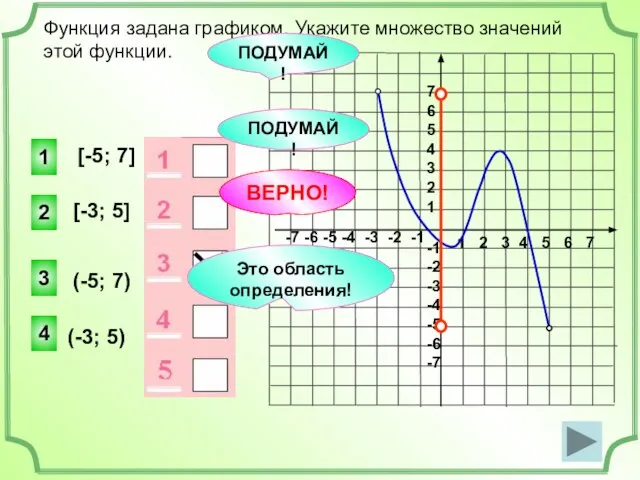
Функция задана графиком.
Укажите область определения
этой функции.
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
[-2; 4]
[-5; 5)
[-5; 5]
(-2; 4]
2
1
3
4
ПОДУМАЙ!
Это множество значений!
ПОДУМАЙ!
ВЕРНО!
Математический диктант

1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком. Укажите множество значений этой функции.
[-5; 7]
(-5; 7)
[-3; 5]
(-3; 5)
3
1
2
4
Это область определения!
ПОДУМАЙ!
ПОДУМАЙ!
ВЕРНО!

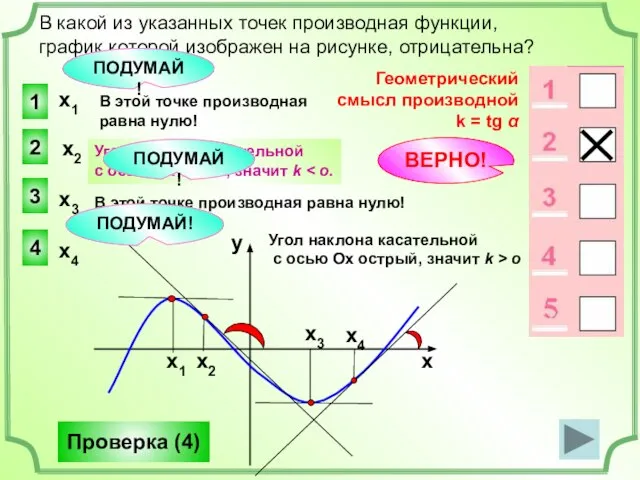
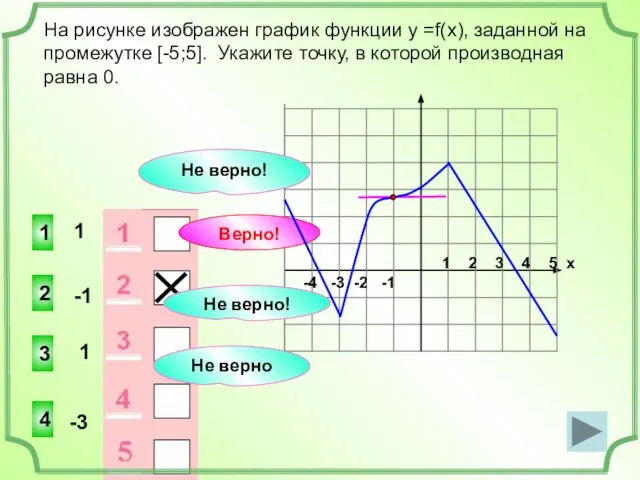
х1
2
1
3
4
В какой из указанных точек производная функции,
график которой изображен на рисунке, отрицательна?
х2
х3
х4
Угол наклона касательной
с осью Ох тупой, значит k < o.
Проверка (4)
х3
х
у
х4
х2
В этой точке производная
равна нулю!
В этой точке производная равна нулю!
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
х1
Геометрический
смысл производной
k = tg α
Угол наклона касательной
с осью Ох острый, значит k > o
ВЕРНО!

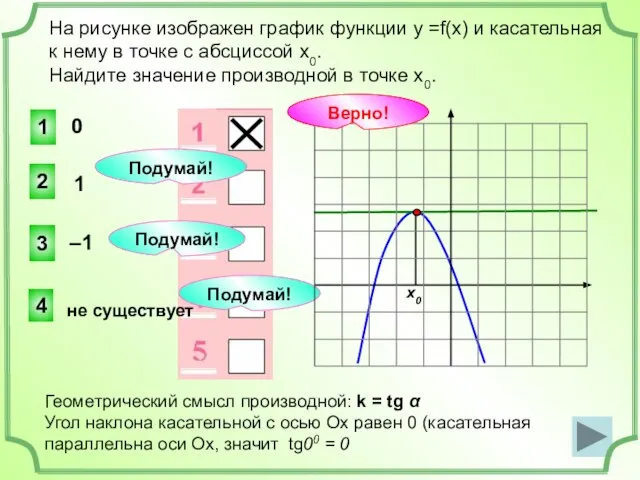
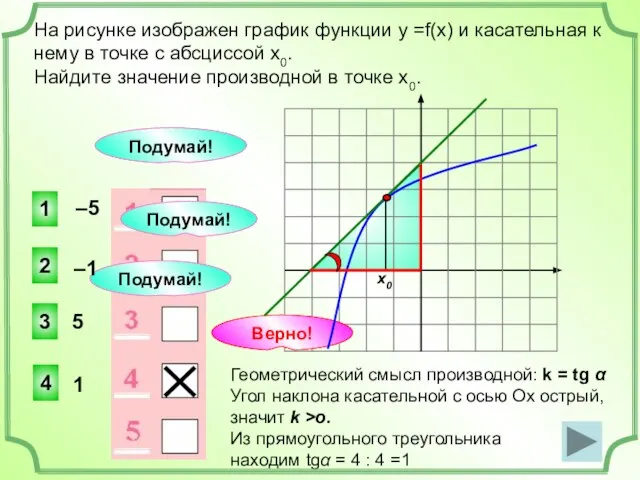
На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.
1
3
4
2
Подумай!
Подумай!
Подумай!
х0
Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох равен 0 (касательная параллельна оси Ох, значит tg00 = 0
0
1
–1
не существует
Верно!

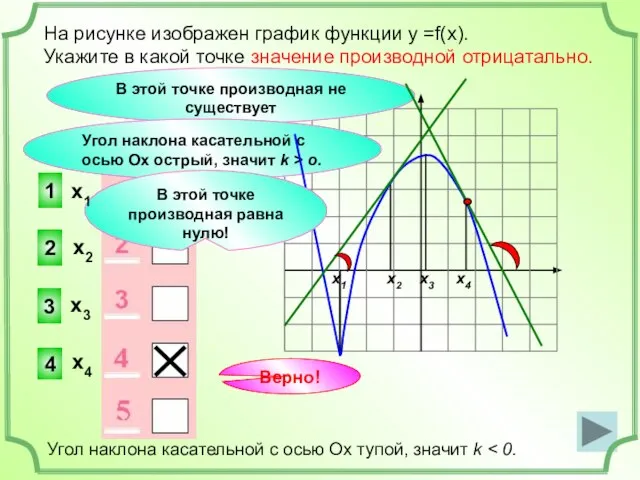
На рисунке изображен график функции у =f(x).
Укажите в какой точке значение производной отрицатально.
4
2
3
В этой точке производная не существует
Верно!
Угол наклона касательной с осью Ох острый, значит k > o.
х1 х2 х3 х4
Угол наклона касательной с осью Ох тупой, значит k < 0.
1
В этой точке производная равна нулю!
х1
х2
х3
х4

-4 -3 -2 -1
1 2 3 4 5 х
На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку, в которой производная равна 0.
2
3
4
1
Не верно!
Не верно
Верно!
Не верно!
1
-1
1
-3

1
4
3
3
Непрерывная функция у = f(x) задана на отрезке [a;b]
На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох.
Проверка
y = f(x)
y
x
2
11
8
Подумай!
Подумай!
Подумай!
Верно!
5
a
b

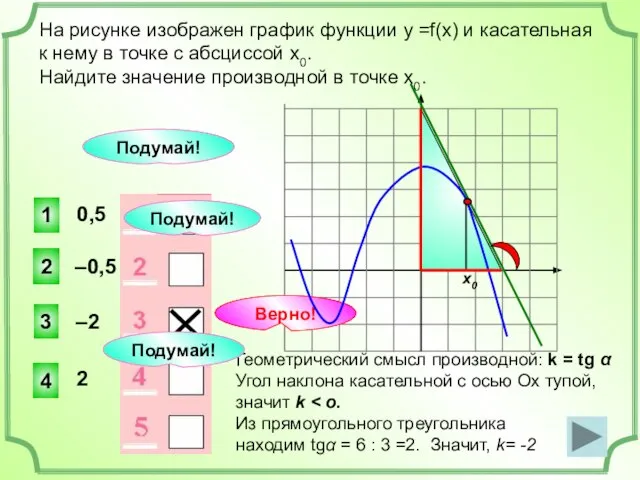
На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.
4
2
3
1
Подумай!
Подумай!
Верно!
Подумай!
х0
Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох острый, значит k >o.
Из прямоугольного треугольника
находим tgα = 4 : 4 =1
–5
–1
5
1

Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох тупой, значит k < o.
Из прямоугольного треугольника
находим tgα = 6 : 3 =2. Значит, k= -2
На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х0.
Найдите значение производной в точке х0.
3
2
4
1
Подумай!
Подумай!
Верно!
Подумай!
х0
0,5
–0,5
–2
2