Содержание
- 2. Общие сведения об устойчивости элементов и систем Расчет внецентренно сжатых элементов
- 3. УСТОЙЧИВОСТЬ КОНСТРУКЦИИ Устойчивость – способность конструкции сопротивляться резкому изменению формы или положения. Потеря устойчивости – резкое
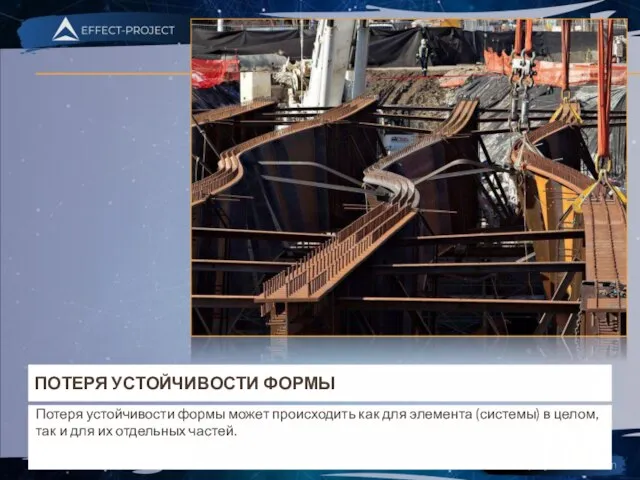
- 4. ПОТЕРЯ УСТОЙЧИВОСТИ ФОРМЫ Потеря устойчивости формы может происходить как для элемента (системы) в целом, так и
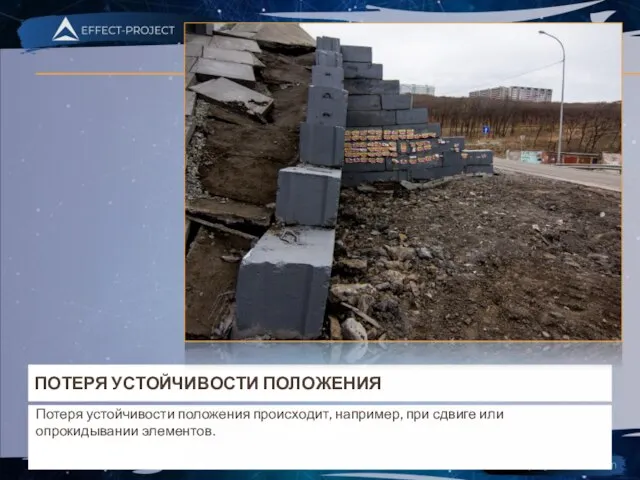
- 5. ПОТЕРЯ УСТОЙЧИВОСТИ ПОЛОЖЕНИЯ Потеря устойчивости положения происходит, например, при сдвиге или опрокидывании элементов.
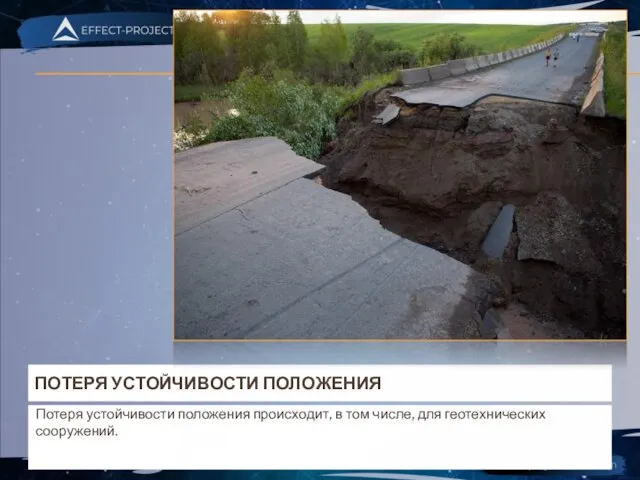
- 6. ПОТЕРЯ УСТОЙЧИВОСТИ ПОЛОЖЕНИЯ Потеря устойчивости положения происходит, в том числе, для геотехнических сооружений.
- 7. ПОТЕРЯ ОБЩЕЙ УСТОЙЧИВОСТИ Потеря устойчивости может происходить для всего сооружения в целом.
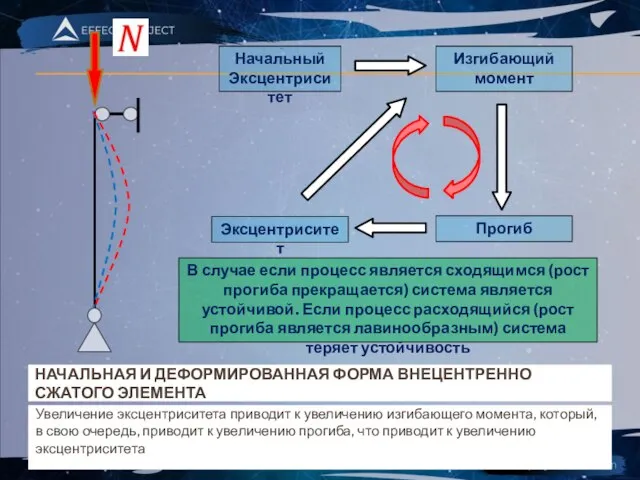
- 8. НАЧАЛЬНАЯ И ДЕФОРМИРОВАННАЯ ФОРМА ВНЕЦЕНТРЕННО СЖАТОГО ЭЛЕМЕНТА Увеличение эксцентриситета приводит к увеличению изгибающего момента, который, в
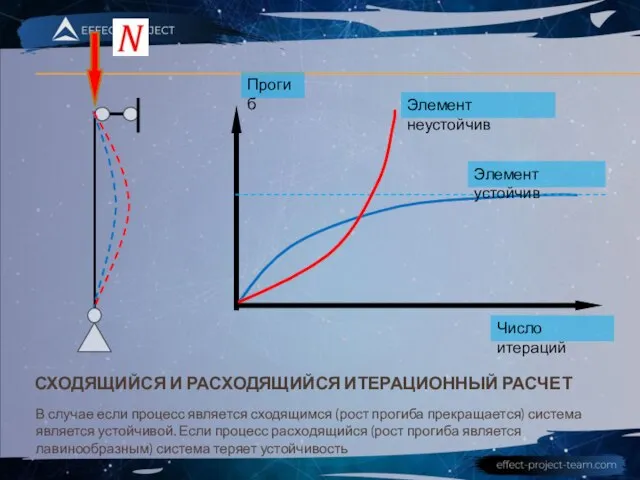
- 9. СХОДЯЩИЙСЯ И РАСХОДЯЩИЙСЯ ИТЕРАЦИОННЫЙ РАСЧЕТ В случае если процесс является сходящимся (рост прогиба прекращается) система является
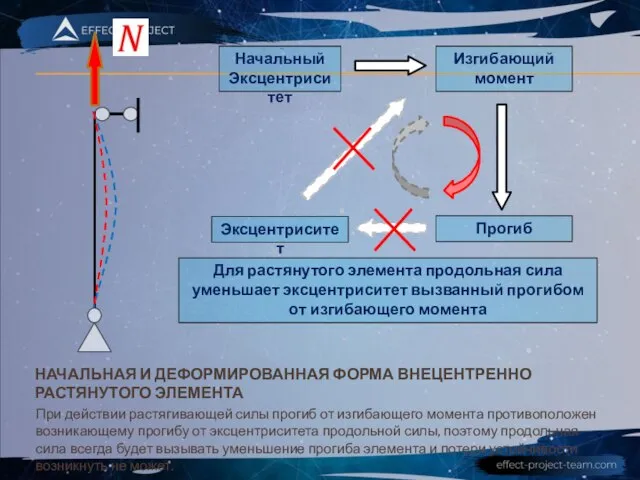
- 10. НАЧАЛЬНАЯ И ДЕФОРМИРОВАННАЯ ФОРМА ВНЕЦЕНТРЕННО РАСТЯНУТОГО ЭЛЕМЕНТА При действии растягивающей силы прогиб от изгибающего момента противоположен
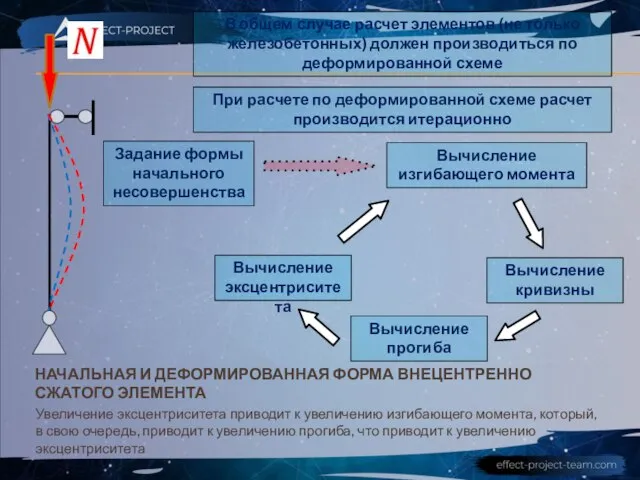
- 11. НАЧАЛЬНАЯ И ДЕФОРМИРОВАННАЯ ФОРМА ВНЕЦЕНТРЕННО СЖАТОГО ЭЛЕМЕНТА Увеличение эксцентриситета приводит к увеличению изгибающего момента, который, в
- 12. НАЧАЛЬНАЯ И ДЕФОРМИРОВАННАЯ ФОРМА ВНЕЦЕНТРЕННО СЖАТОГО ЭЛЕМЕНТА Расчет устойчивости по деформированной схеме может производиться только при
- 13. ПРЕИМУЩЕСТВА И НЕДОСТАТКИ РАСЧЕТА ПО ДЕФОРМИРОВАННОЙ СХЕМЕ Преимущества расчета по деформированной схеме: Расчет элементов любой формы,
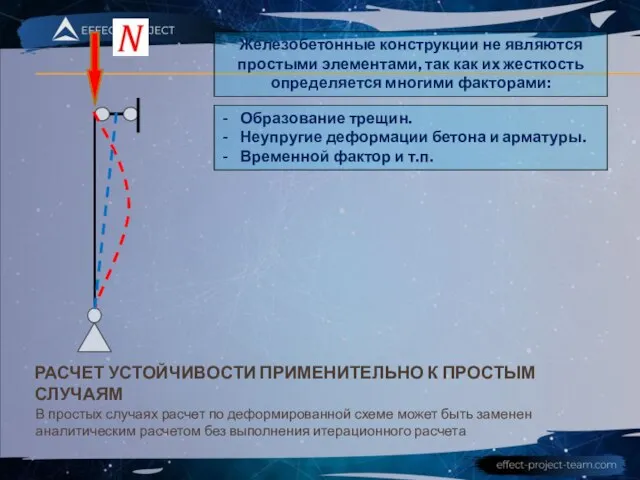
- 14. РАСЧЕТ УСТОЙЧИВОСТИ ПРИМЕНИТЕЛЬНО К ПРОСТЫМ СЛУЧАЯМ В простых случаях расчет по деформированной схеме может быть заменен
- 15. РАСЧЕТ УСТОЙЧИВОСТИ ПРИМЕНИТЕЛЬНО К ПРОСТЫМ СЛУЧАЯМ В простых случаях расчет по деформированной схеме может быть заменен
- 16. Потеря устойчивости По упругой схеме По неупругой схеме В сечении элемента не наступает неупругих деформаций. Характерно
- 17. УПРУГАЯ И НЕУПРУГАЯ ПОТЕРЯ УСТОЙЧИВОСТИ Для теоретического материала бесконечной прочности возможна только потеря устойчивости по упругой
- 18. ТЕРМИН «ПОТЕРЯ УСТОЙЧИВОСТИ» ПРИМЕНИТЕЛЬНО К ЖЕЛЕЗОБЕТОНУ В нормах проектирования отсутствует термин «устойчивость» применительно к железобетону, так
- 20. Скачать презентацию








 Мехатроника и мобильная робототехника
Мехатроника и мобильная робототехника Comfort lir oil. Масло, которое заботится о ваших губах
Comfort lir oil. Масло, которое заботится о ваших губах Where is the?
Where is the? Политическая культура и поведение
Политическая культура и поведение Жизненный цикл человеческого капитала. Тема 3
Жизненный цикл человеческого капитала. Тема 3 Презентация на тему: The wonderful world of animals
Презентация на тему: The wonderful world of animals Анализ работы МОУ «СОШ №11» за 2010-2011 учебный год
Анализ работы МОУ «СОШ №11» за 2010-2011 учебный год Район проживания
Район проживания Чешки для вашего ребенка
Чешки для вашего ребенка Интерактивные среды на уроке математики
Интерактивные среды на уроке математики First aid
First aid  Абстракционизм – гармония беспредметности
Абстракционизм – гармония беспредметности Третья сессия Молодёжного парламента II созыва при Совете депутатов МО Камбарский район
Третья сессия Молодёжного парламента II созыва при Совете депутатов МО Камбарский район Иван Сергеевич Соколов-Микитов
Иван Сергеевич Соколов-Микитов Лагерь отдыха Радуга
Лагерь отдыха Радуга Foot
Foot Презентация на тему Государственное регулирование ценообразования в Российской Федерации
Презентация на тему Государственное регулирование ценообразования в Российской Федерации  Lektsia_1
Lektsia_1 Жисмоний шахс ер мулк соликлар
Жисмоний шахс ер мулк соликлар Лабораторная работа №1
Лабораторная работа №1 Сечения
Сечения Лекции_3_и_4. Сравнительный подход
Лекции_3_и_4. Сравнительный подход Обоснование методов пуска асинхронных двигателей в электрических сетях малой мощности
Обоснование методов пуска асинхронных двигателей в электрических сетях малой мощности «Нерастущий рынок – ожидаемое событие» Николай Имамбаев экс-президент Российской ассоциации производителей и дилеров замочно
«Нерастущий рынок – ожидаемое событие» Николай Имамбаев экс-президент Российской ассоциации производителей и дилеров замочно Диета
Диета Есть ли дубы в Сибири?
Есть ли дубы в Сибири? Развивающее движение
Развивающее движение Музыкально-дидактические игры для дошкольников
Музыкально-дидактические игры для дошкольников