Содержание
- 2. RELATION A Relation A relation is a correspondence between a first set, called the domain, and
- 3. FUNCTIONS B Functions are special relations. Every set of ordered pairs is a relation, but every
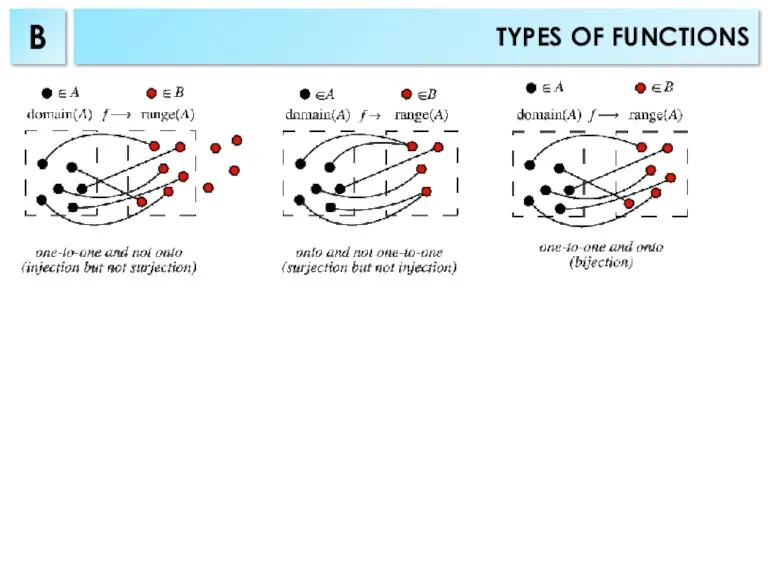
- 4. TYPES OF FUNCTIONS B
- 5. Surjective Injective Bijective A function is bijective (one-to-one and onto or one-to-one correspondence) if every element
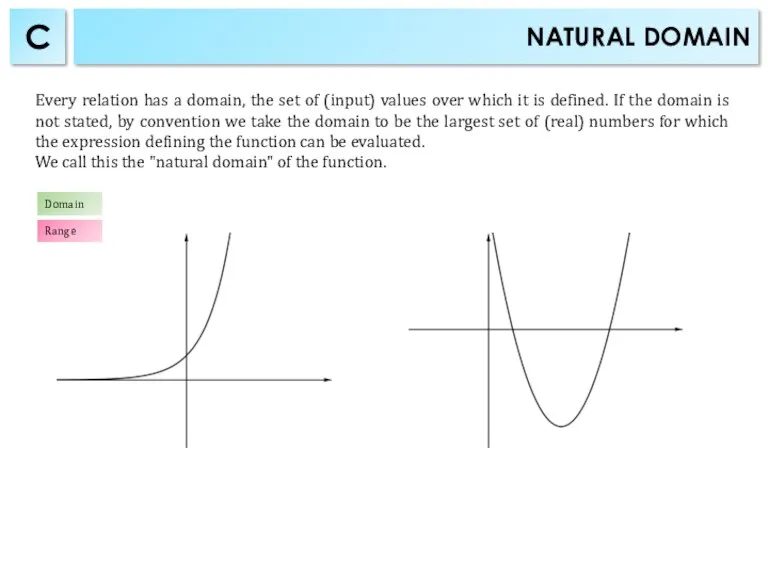
- 6. NATURAL DOMAIN C Every relation has a domain, the set of (input) values over which it
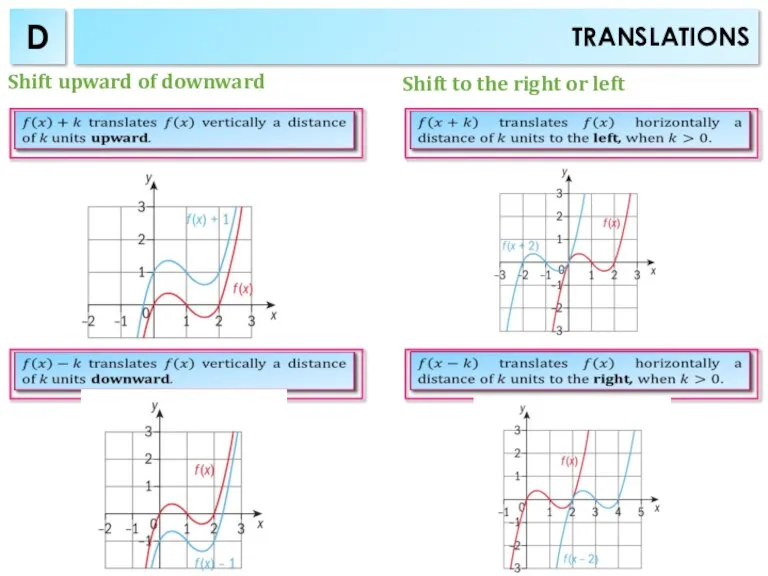
- 7. TRANSLATIONS D Shift upward of downward Shift to the right or left
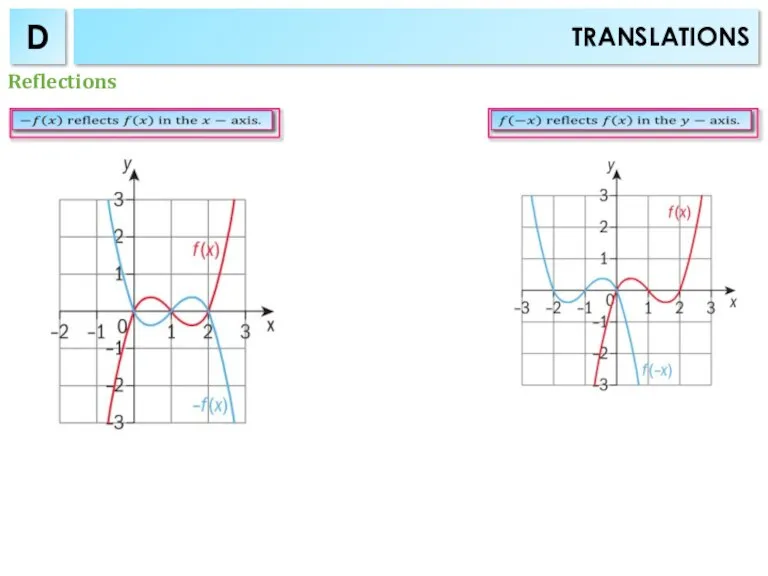
- 8. TRANSLATIONS D Reflections
- 10. Скачать презентацию



 Презентация на тему Национальные символы Великобритании, США, России
Презентация на тему Национальные символы Великобритании, США, России  Spelling sound pattern -ar
Spelling sound pattern -ar What’s missing?
What’s missing? Manual for reports
Manual for reports Презентация на тему Professions 5 класс
Презентация на тему Professions 5 класс  London
London Visuals: how much, how often, which ones and what for?
Visuals: how much, how often, which ones and what for? Презентация на тему Children and parents (Дети и родители)
Презентация на тему Children and parents (Дети и родители)  Презентация на тему The Royal Family
Презентация на тему The Royal Family  Animals. Внеклассное мероприятие для 4 класса
Animals. Внеклассное мероприятие для 4 класса Success
Success Winter presentation
Winter presentation Halloween speaking
Halloween speaking Dora at the waterfall
Dora at the waterfall Reported questions
Reported questions Crazy time machine. Past simple negative
Crazy time machine. Past simple negative My town in the past
My town in the past English animals
English animals Merry Christmas and Happy New Year
Merry Christmas and Happy New Year Indian English
Indian English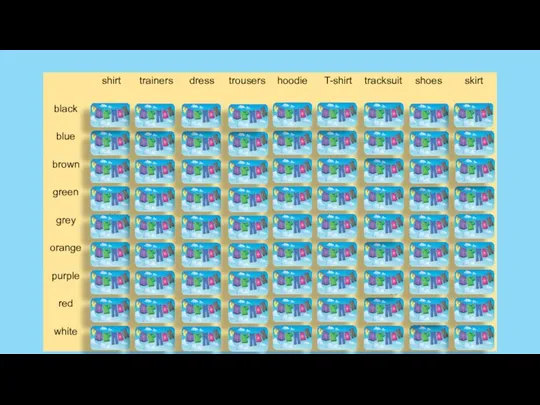 Clothes colours is are
Clothes colours is are Путешествие в Волшебную страну
Путешествие в Волшебную страну Italian. Итальянец
Italian. Итальянец Тема: Развитие творческих способностей учащихся начальной школы в процессе изучения английского языка
Тема: Развитие творческих способностей учащихся начальной школы в процессе изучения английского языка  Animals flashcards
Animals flashcards Identifying an expanded noun phrase in a sentence quiz
Identifying an expanded noun phrase in a sentence quiz Choose the right word and translate the text
Choose the right word and translate the text Telling the time
Telling the time