Содержание
- 2. Из-за осевого вращения Земли звезды нам кажутся перемещающимися по небу Явления суточного движения звезд удобно изучать,
- 3. Небесная сфера - воображаемая сфера произвольного радиуса, на которую проецируются небесные светила За центр небесной сферы,
- 4. У древних народов: наличие реальной сферы, ограничивающей весь мир и несущей на своей поверхности многочисленные звёзды
- 5. Важнейшие точки и дуги на небесной сферы Отвесная линия (или вертикальная линия) • Z' Z О
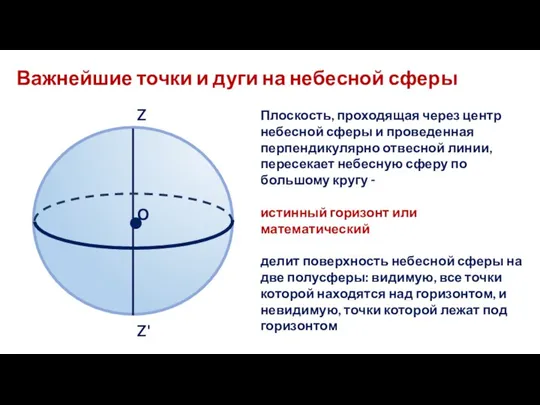
- 6. Важнейшие точки и дуги на небесной сферы Плоскость, проходящая через центр небесной сферы и проведенная перпендикулярно
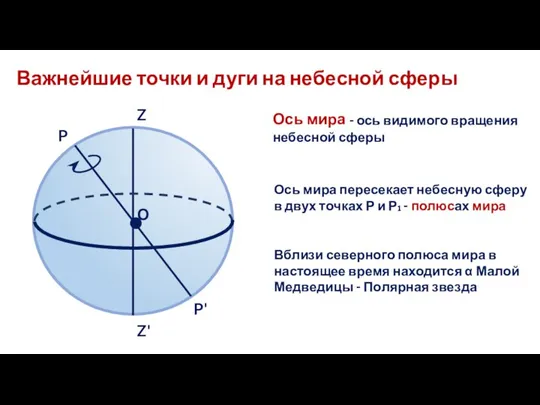
- 7. Важнейшие точки и дуги на небесной сферы Ось мира - ось видимого вращения небесной сферы Вблизи
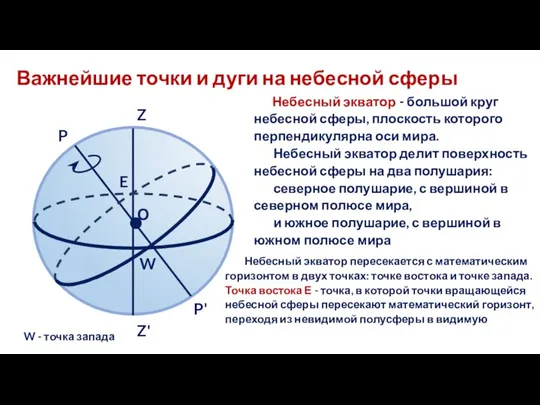
- 8. Важнейшие точки и дуги на небесной сферы Небесный экватор - большой круг небесной сферы, плоскость которого
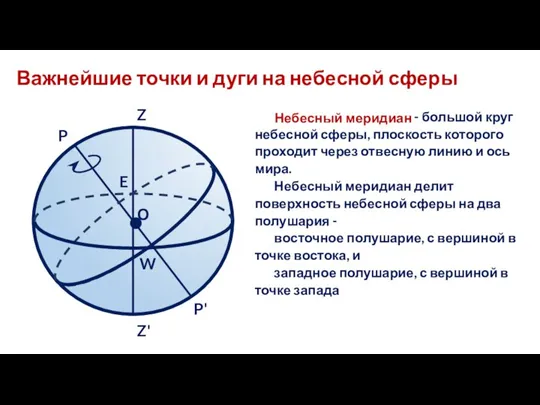
- 9. Важнейшие точки и дуги на небесной сферы Небесный меридиан - большой круг небесной сферы, плоскость которого
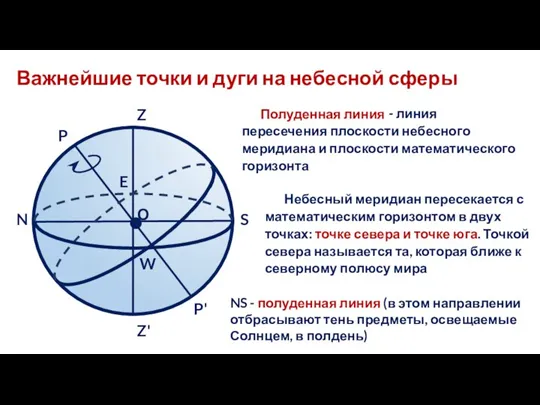
- 10. Важнейшие точки и дуги на небесной сферы Небесный меридиан пересекается с математическим горизонтом в двух точках:
- 11. Важнейшие точки и дуги на небесной сферы • Z' Z О P' P N S E
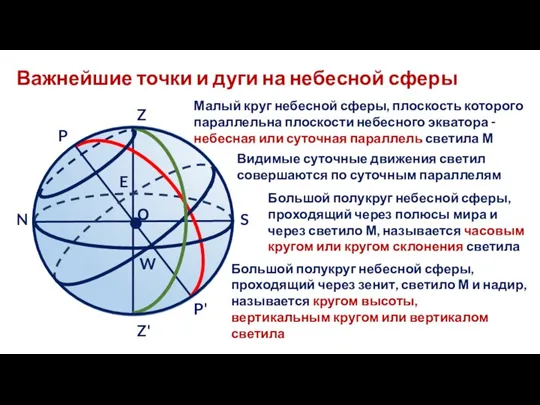
- 12. Важнейшие точки и дуги на небесной сферы Z' Z О P' P N S E W
- 13. Важнейшие точки и дуги на небесной сферы Z' Z О P' P N S E W
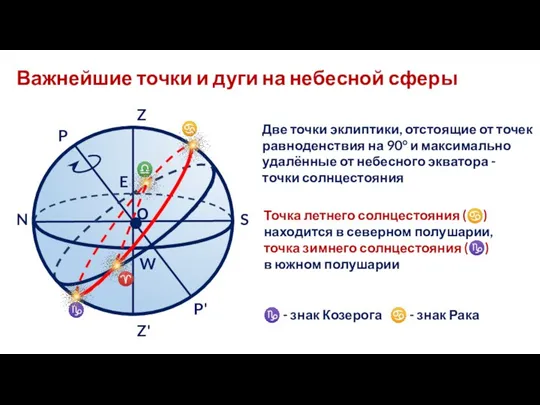
- 14. Важнейшие точки и дуги на небесной сферы Z' Z О P' P N S E W
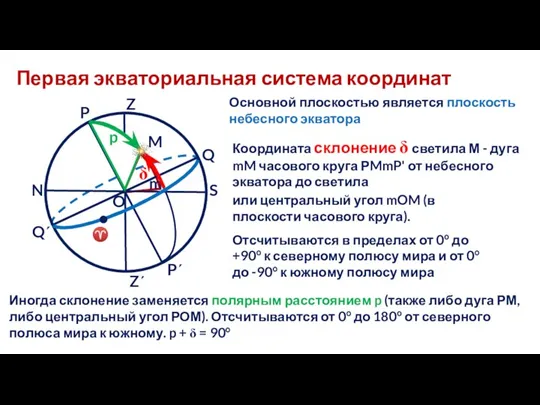
- 15. Первая экваториальная система координат Основной плоскостью является плоскость небесного экватора Иногда склонение заменяется полярным расстоянием p
- 16. Первая экваториальная система координат N S Q Q΄ O Z Z΄ P P΄ M m t
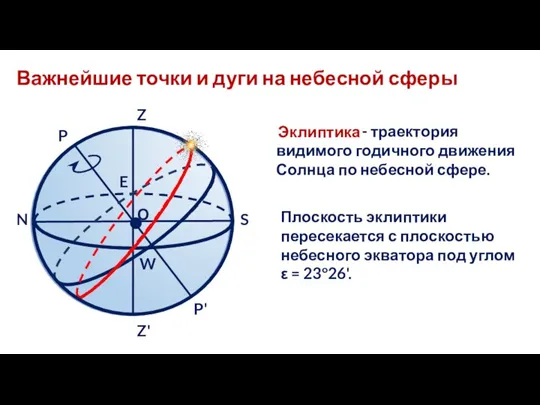
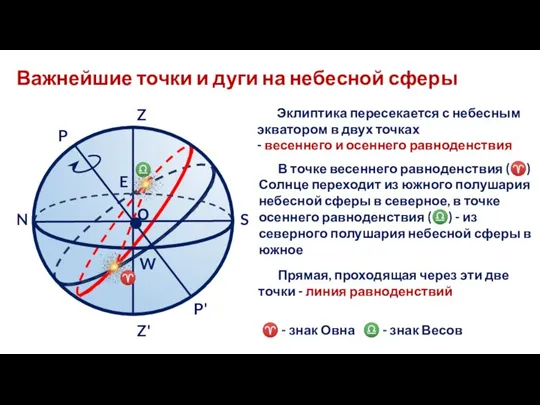
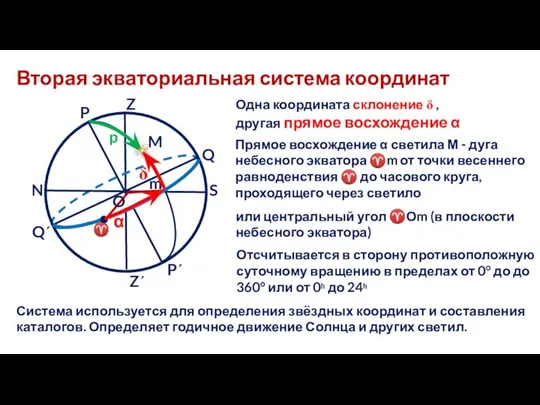
- 17. Вторая экваториальная система координат N S Q Q΄ Z Z΄ P P΄ M m ♈ p
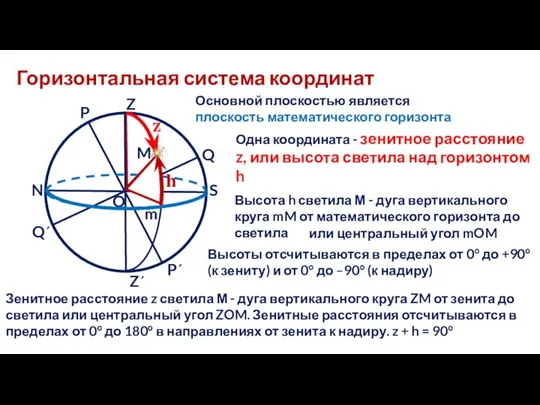
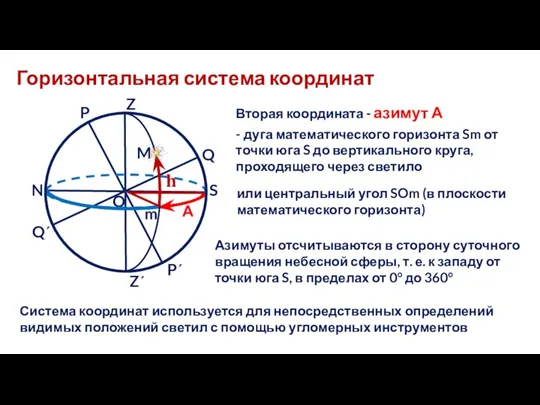
- 18. Горизонтальная система координат N S Q Q΄ O Z Z΄ P P΄ M Основной плоскостью является
- 19. Горизонтальная система координат N S Q Q΄ O Z Z΄ P P΄ M m h Вторая
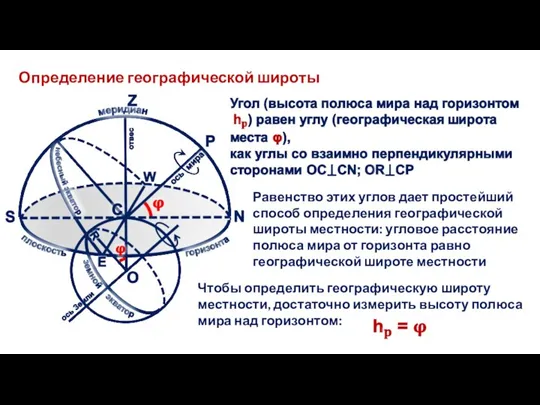
- 20. Определение географической широты Равенство этих углов дает простейший способ определения географической широты местности: угловое расстояние полюса
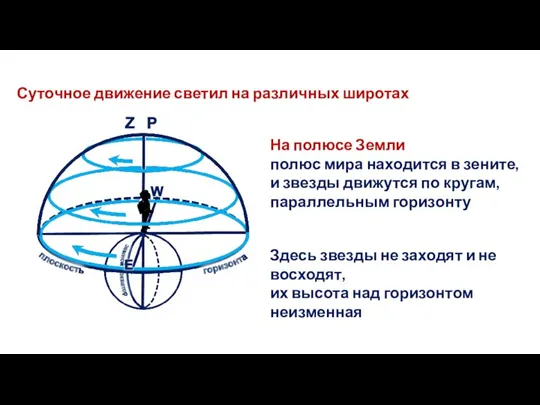
- 21. Суточное движение светил на различных широтах На полюсе Земли полюс мира находится в зените, и звезды
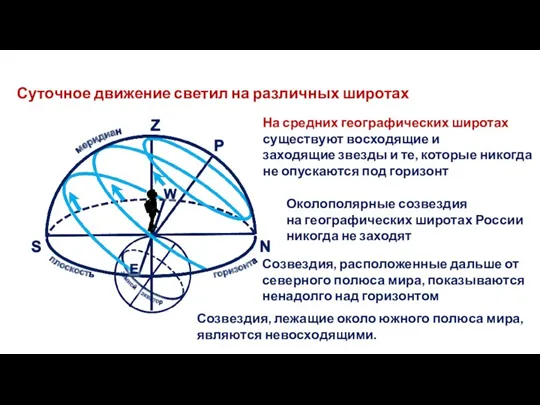
- 22. Суточное движение светил на различных широтах Околополярные созвездия на географических широтах России никогда не заходят На
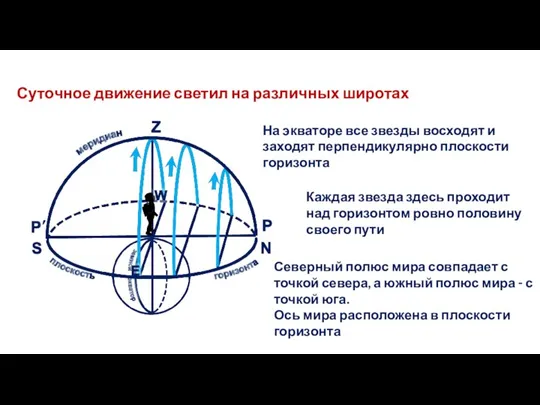
- 23. Суточное движение светил на различных широтах На экваторе все звезды восходят и заходят перпендикулярно плоскости горизонта
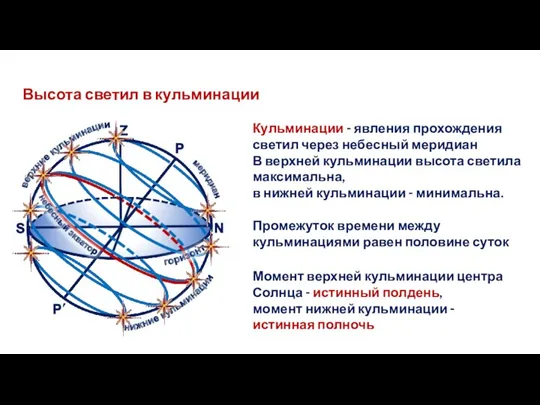
- 24. Высота светил в кульминации Кульминации - явления прохождения светил через небесный меридиан В верхней кульминации высота
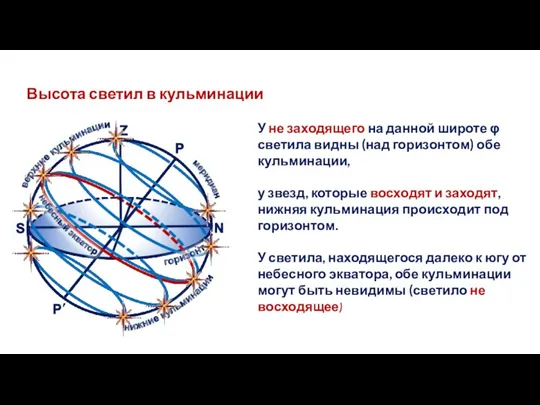
- 25. Высота светил в кульминации У не заходящего на данной широте φ светила видны (над горизонтом) обе
- 26. S N P Pʹ Z Zʹ Q Qʹ M φ 90°- φ δ h O h
- 28. Скачать презентацию






 Марс. Таинственная красная планета
Марс. Таинственная красная планета Развитие научных знаний. Теория коперника
Развитие научных знаний. Теория коперника Физическая природа звезд. Расстояние до звезд
Физическая природа звезд. Расстояние до звезд Среди звезд и галактик
Среди звезд и галактик Калейдоскоп интересных фактов Нас согреет тёплый лучик
Калейдоскоп интересных фактов Нас согреет тёплый лучик Этот необъятный космос
Этот необъятный космос ОНИОО Космопоиск. Памятка очевидцу при наблюдении НЛО
ОНИОО Космопоиск. Памятка очевидцу при наблюдении НЛО Планета Меркурий
Планета Меркурий Космический словарь
Космический словарь Созвездие Большой пес
Созвездие Большой пес Время и календарь
Время и календарь Эра космонавтики - презентация по Астрономии _
Эра космонавтики - презентация по Астрономии _ Жизнь и разум во Вселенной
Жизнь и разум во Вселенной Презентация на тему Пульсары
Презентация на тему Пульсары  Нейросетевой способ классификации искусственных спутников Земли по параметрам их орбит
Нейросетевой способ классификации искусственных спутников Земли по параметрам их орбит День космонавтики
День космонавтики Интересные факты из жизни космонавтов
Интересные факты из жизни космонавтов Солнце, внутреннее строение (10 класс)
Солнце, внутреннее строение (10 класс) Космический корабль Восток
Космический корабль Восток Горизонтальная система координат
Горизонтальная система координат Диаграмма Гершпрунга-Рессела (спектр-светимость)
Диаграмма Гершпрунга-Рессела (спектр-светимость) Смена дня и ночи
Смена дня и ночи Темная Вселенная
Темная Вселенная УТЭК. Астрономия
УТЭК. Астрономия Планета Венера
Планета Венера Звёзды и созвездия
Звёзды и созвездия Гагарин.Викторина
Гагарин.Викторина Планеты. 4 класс
Планеты. 4 класс