000) м
∙ 1961 г. (149 599 500 000 ± 800 000) м
∙ 1998 г. (149 597 870 691 ± 2) м
∙ 1999 г. (149 597 870 691.0 ± 1.0) м
∙ 1999 г. (149 597 870 691.1 ± 0.2) м
149 504 312 000 ± 170 400 000 м
РАДИОЛОКАЦИЯ ПЛАНЕТ
В 1946г первая радиолокация Луны.
В 1957-1963гг — радиолокация Солнца,
Меркурия (с 1962г), Венеры (с 1961г),
Марса и Юпитера (с 1964г), Сатурна (с 1973г) в Великобритании, СССР и США.
импульс→объект →отраженный сигнал→время
VЭМВ=С=299792458м/с≈3*108 м/с.
Предложен советскими физиками
Л.И. Мандельштам и Н.Д. Папалекси
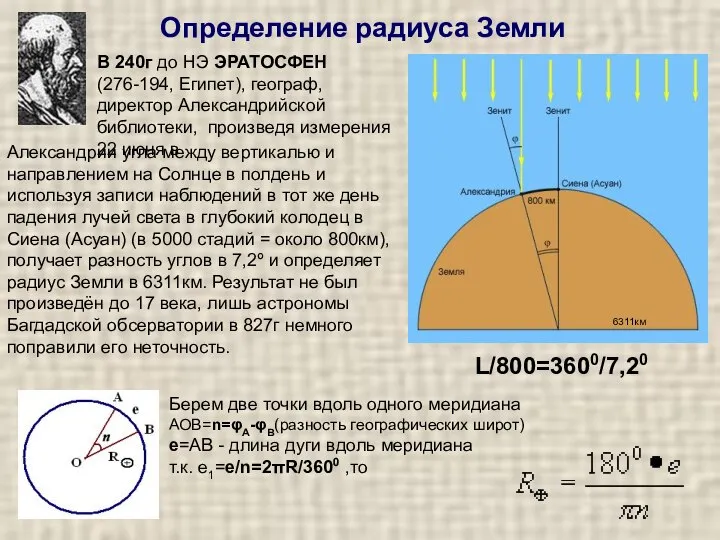
Определение астрономической единицы
НАЗЕМНАЯ ОПТИЧЕСКАЯ АСТРОМЕТРИЯ
Расположение лазерных уголковых отражателей на Луне. Все, за исключением отражателя Лунохода-1 (L1), работают и сейчас
Более точная лазерная локация проводится с 1969г
1 а. е.=149 597 870 691 ± 6м ≈149,6 млн.км






 Презентация на тему Сатурн - властелин колец
Презентация на тему Сатурн - властелин колец  Человек в космосе
Человек в космосе Планета Марс
Планета Марс Каким должен быть дом колониста на Марсе?
Каким должен быть дом колониста на Марсе? Планеты земной группы для ЭЖД. Урок 15
Планеты земной группы для ЭЖД. Урок 15 Планета Земля
Планета Земля Калейдоскоп интересных фактов Нас согреет тёплый лучик
Калейдоскоп интересных фактов Нас согреет тёплый лучик Урок технологии
Урок технологии Строение и масштабы Вселенной (1)
Строение и масштабы Вселенной (1)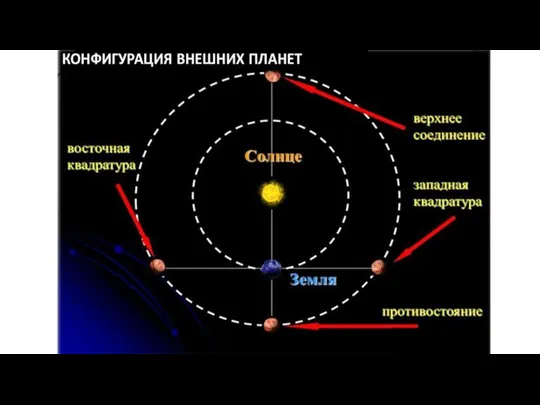 Конфигурации внутренних и внешних планет
Конфигурации внутренних и внешних планет Законы Кеплера
Законы Кеплера Чёрные дыры. 9 класс
Чёрные дыры. 9 класс Удивительный мир космоса
Удивительный мир космоса Законы движения небесных тел. Тема 3
Законы движения небесных тел. Тема 3 Презентация на тему Джордано Бруно
Презентация на тему Джордано Бруно  Презентация на тему Кометы
Презентация на тему Кометы  ОНИОО Космопоиск. Памятка очевидцу при наблюдении НЛО
ОНИОО Космопоиск. Памятка очевидцу при наблюдении НЛО Звёздные узоры
Звёздные узоры Планеты-гиганты, их спутники и кольца
Планеты-гиганты, их спутники и кольца Планеты далекие и близкие
Планеты далекие и близкие Презентация на тему Земля и Луна
Презентация на тему Земля и Луна  Презентация на тему Теории Коперника
Презентация на тему Теории Коперника  День космонавтики
День космонавтики Земляв ладонях. Космонавтике посвящается
Земляв ладонях. Космонавтике посвящается Зачем нужно осваивать космос
Зачем нужно осваивать космос Удивительные снимки из стратосферы
Удивительные снимки из стратосферы Планета Земля
Планета Земля Деймос. Естественный спутник Марса
Деймос. Естественный спутник Марса