Содержание
- 2. Популяция – сообщество особей одного вида, занимающих некоторую область пространства планеты (бактерии, вирусы, различные виды насекомых,
- 3. Как будет изменяться численность популяции, если сдерживающие факторы (болезни, хищники, конкурирующие виды, ограниченность питания и т.д.)
- 4. Математическая постановка:
- 6. Модель безымунной эпидемии
- 7. Задание по Расчетной работе № 2. С помощью пакета «Wolfram Mathematica» Для модели Мальтуса получить аналитическое
- 8. Требуется найти функцию y(t), удовлетворяющую дифференциальному уравнению где f(t, y(t)) – заданная непрерывная функцию двух аргументов.
- 9. Метод Эйлера Заменим производную функции в точке разностным аналогом: Тогда дифференциальное уравнение можно заменить разностным: Окончательно
- 11. Скачать презентацию








 Питание растений
Питание растений Мышцы нижней конечности
Мышцы нижней конечности Презентация на тему Антропосоциогенез
Презентация на тему Антропосоциогенез  Презентация на тему Приспособленность организмов – результат эволюции
Презентация на тему Приспособленность организмов – результат эволюции  动物 dòngwù
动物 dòngwù Актуализация знаний. Лишайники
Актуализация знаний. Лишайники Бамбук звичайний
Бамбук звичайний Система автоматического полива. Насос
Система автоматического полива. Насос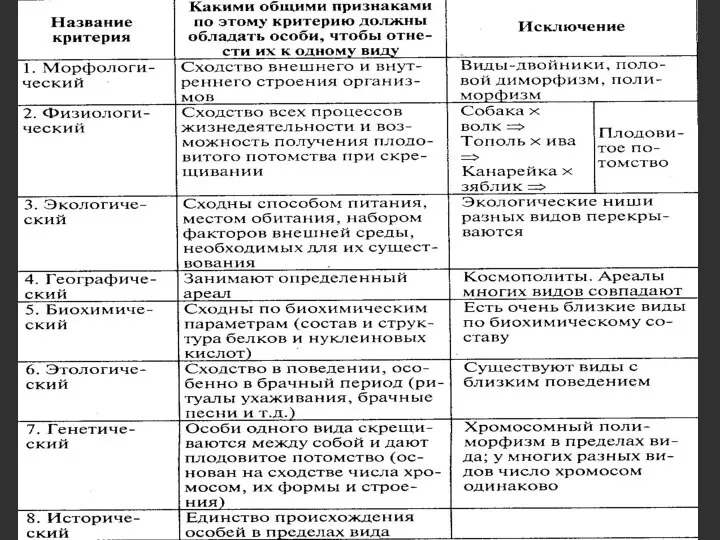 Таблица - Критерии вида
Таблица - Критерии вида Явления природы. 2 класс
Явления природы. 2 класс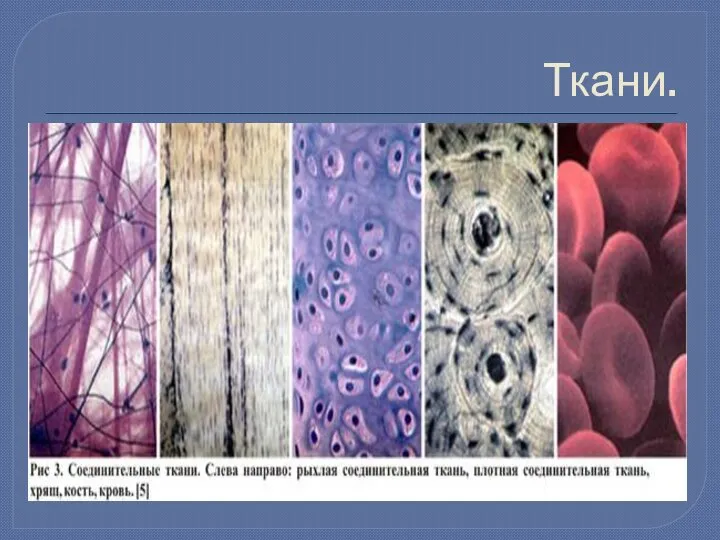 Ткани. Эпителиальные покровные ткани
Ткани. Эпителиальные покровные ткани Энзимология III. Регуляция активности
Энзимология III. Регуляция активности Животные водоема
Животные водоема Введение в генетику
Введение в генетику Полимеризация ядер. Олигомеризация ядерного аппарата
Полимеризация ядер. Олигомеризация ядерного аппарата Строение и функции нервной системы. Принципы изучения механизмов ее деятельности
Строение и функции нервной системы. Принципы изучения механизмов ее деятельности Фотосинтез . 6 класс
Фотосинтез . 6 класс Бесполое и половое размножение животных и растений
Бесполое и половое размножение животных и растений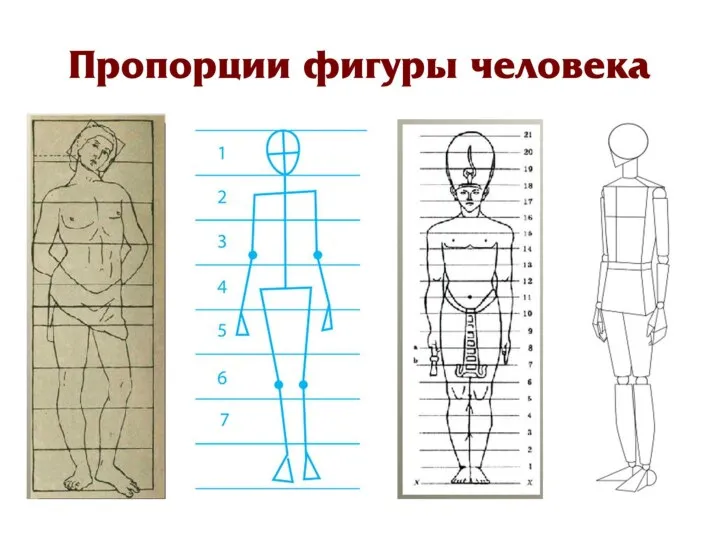 Пропорции фигуры человека
Пропорции фигуры человека Цепь переноса электронов. Лекция №8
Цепь переноса электронов. Лекция №8 Померанский шпиц
Померанский шпиц Вклад отечественных ученых в развитие биологии
Вклад отечественных ученых в развитие биологии Вомбати
Вомбати Покрытосеменные растения
Покрытосеменные растения Влияние антибиотиков на организм человека. 10 класса
Влияние антибиотиков на организм человека. 10 класса Презентация на тему Агроэкосистемы
Презентация на тему Агроэкосистемы 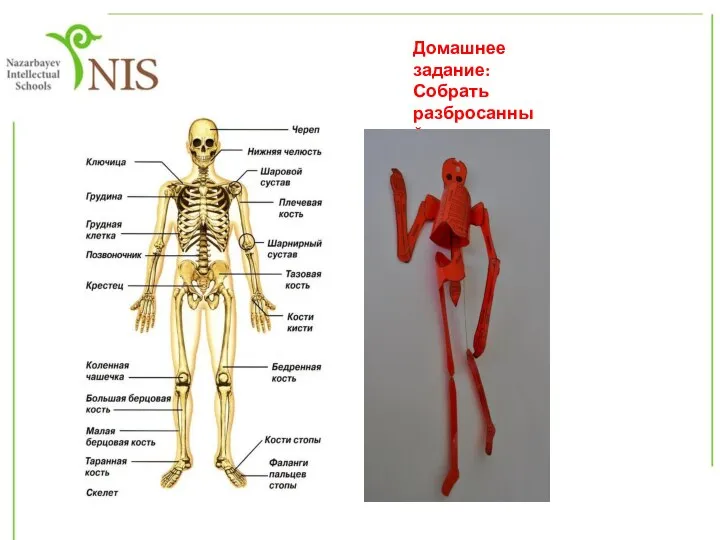 Макростроение костей
Макростроение костей Многообразие насекомых, их роль в природе и практическое значение
Многообразие насекомых, их роль в природе и практическое значение