Содержание
- 2. 1. Общие понятия об индексах «Индекс» в переводе с латинского — указатель или показатель. В статистике
- 3. Индекс — это относительная величина сравнения, которая характеризует изменение социально-экономических явлений и процессов во времени, в
- 4. Методология построения и использования индексов в статистико-экономическом анализе называется индексным методом. Важной особенностью индексов является то,
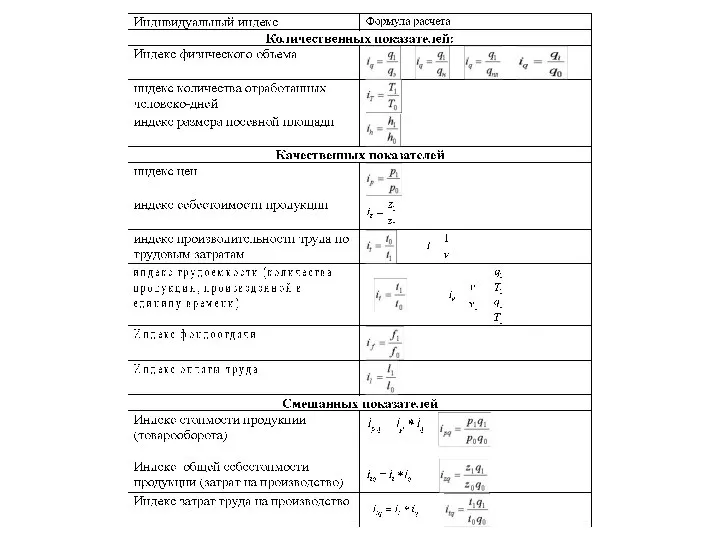
- 5. В индексном методе применяется определенная система условных обозначений, посредством которых строят и записывают индексы. а) количественные
- 6. б) качественные показатели: р — цена единицы товара или продукции; z — себестоимость единицы продукции; -
- 7. в) показатели, которые получены путем произведения качественного и количественного показателей: рq — стоимость выпуска продукции или
- 8. В использовании индексов при динамических или пространственных сравнениях используют специальные обозначения. Период или объект, с которым
- 9. В индексах имеются две величины: одну, изменение которой изучают при использовании индивидуальных и общих индексов, называют
- 10. 2. Классификация индексов Индексы могут быть классифицированы по таким признакам: а) мера охвата элементов совокупности; б)
- 11. а) По мере охвата элементов совокупности различают индивидуальные и общие (сводные) индексы. Индивидуальные индексы — это
- 12. Общие (сводные) индексы обозначают буквой I и характеризуют динамику сложного явления, элементы которого не поддаются непосредственному
- 13. б) По базе сравнения различают базисные и цепные индексы. в) По виду объекта сравнения различают динамические,
- 14. д) По форме построения в зависимости от методологии расчета общие (сводные) индексы разделяют на агрегатные и
- 15. з) По объекту исследования индексы количественных показателей разделяют на индексы физического объема продукции, производительности труда, стоимости
- 16. Индексы, в которых изменяется одна величина, называют индексами постоянного состава (индексы цен, себестоимость и др.), а
- 17. 3. Индивидуальные индексы Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во
- 19. Индивидуальные индексы могут рассчитываться в виде индексного ряда за несколько периодов. При этом существует два способа
- 20. Для индекса физического объема продукции цепные индексы по разным периодами рассчитываются так:
- 21. Между цепными и базисными индивидуальными индексами существует такая взаимосвязь: - произведение цепных индексов равняется базисному индексу
- 22. 4. Агрегатная форма общего индекса. Сущность и принципы построения Агрегатные индексы являются основной формой общего индекса
- 23. В 1764 г. итальянец Карли определил общий индекс цен как среднюю арифметическую простую из индивидуальных индексов
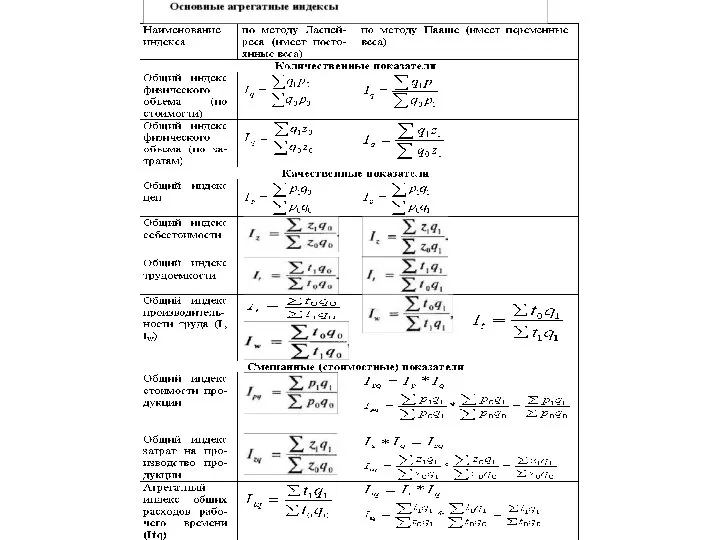
- 25. Агрегатная форма общих индексов количественных показателей Наиболее типичным общим индексом количественных показателей является индекс физического объема
- 26. Изменение цен на продукцию в текущем периоде по сравнению с базисным не влияет на величину индекса.
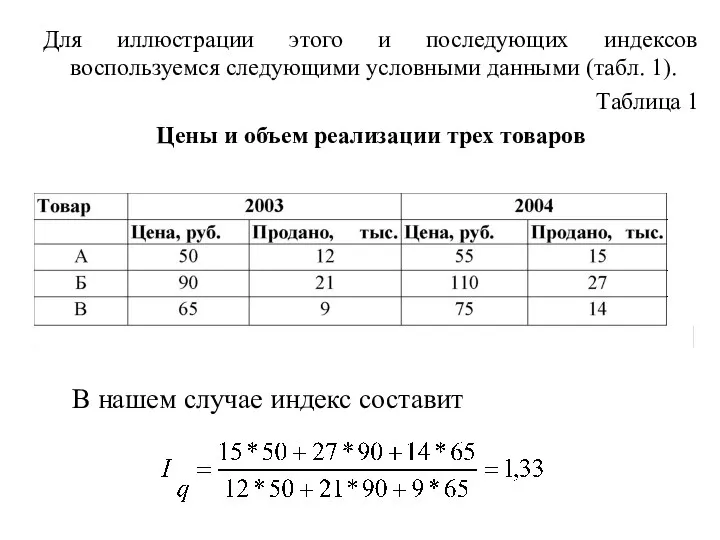
- 27. Обозначения Где q1 – количество одноименных единиц продукции (объем продаж одноименного товара) в отчетном периоде; q0
- 28. Для иллюстрации этого и последующих индексов воспользуемся следующими условными данными (табл. 1). Таблица 1 Цены и
- 29. Агрегатная форма общих индексов качественных и смешанных показателей Среди агрегатных индексов качественных показателей значительная роль отводится
- 30. Индекс Ласпейреса рассчитывается по формуле где Σp1q0 — стоимость продукции в базисном периоде по ценам текущего
- 31. При построении данного индекса цена выступает в качестве индексируемой величины, а количество проданного товара — в
- 32. Разность числителя и знаменателя (Δp = Σp1q1 – Σp0q1) соответствует абсолютной экономии (Δр 0) денежных средств
- 33. Учитывая имеющееся несоответствие между индексами Пааше и Ласпейреса, И. Фишером в международном сопоставлении предложен «идеальный индекс»
- 34. К основным агрегатным индексам смешанных показателей можно отнести индексы стоимости (товарооборота) товаров Ipq, индексы общей себестоимости
- 35. Вернемся к рассмотрению задачи с розничными ценами. Как уже отмечалось, цены различных товаров складывать не правомерно,
- 36. Так как агрегатный индекс стоимости товаров (товарооборота) можно представить как произведение индекса цен Ip (в форме
- 37. Или Рассчитаем индекс товарооборота
- 38. Рассчитанное значение индекса позволяет заключить, что товарооборот в целом по данной товарной группе в 2004 г.
- 39. Агрегатный индекс общих расходов рабочего времени Itq представляется в виде произведения индекса производительности труда It и
- 40. Взаимодействие факторов изменения себестоимости и объемов реализации отражается на значении сводного индекса затрат на производство
- 41. Если для взвешивания значений качественного показателя используется средний объем , то общий индекс называется индексом Лоу.
- 42. 5. Система индексов Индексы позволяют получать сводную оценку изучаемых процессов постоянно, месяц за месяцем, год за
- 43. ■ цепные индексы с постоянными соизмерителями: ■ цепные индексы с переменными соизмерителями:
- 44. ■ базисные индексы с постоянными соизмерителями: ■ базисные индексы с переменными соизмерителями:
- 45. Между цепными и базисными агрегатными индексами существует такая взаимосвязь: для индексов с постоянными соизмерителями 1. произведение
- 46. 2. Частное отделения последующего базисного индекса с постоянными соизмерителями на предыдущей равняется цепному индексу: Или
- 47. 2. Цепные индексы цен с переменными весами имеют следующий вид: При использовании весов базисного периода получаем
- 48. Отметим, что использование постоянных весов более предпочтительно, так как рассчитываемые таким образом индексы мультипликативны, т. е.
- 49. Система базисных индексов с переменными весами имеет следующий вид: Базисные индексы цен с постоянными весами рассчитываются
- 50. С помощью индексов можно определить абсолютный прирост итогового показателя мультипликативной модели как в целом, так и
- 51. 6. Средневзвешенные индексы Существуют две формы средневзвешенных индексов: среднеарифметическая и среднегармоническая. Как правило, средний арифметический индекс
- 52. Средний арифметический индекс тождествен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только
- 53. Средний арифметический индекс физического объема продукции вычисляется по формуле Весами в формуле является стоимость продукции базисного
- 54. В статистике широко известен и другой средний арифметический индекс, который используется при анализе производительности труда. Он
- 55. Индексы других качественных показателей (цен, себестоимости и т. д.) определяются по формуле средней гармонической взвешенной величины.
- 56. Таким образом, весами при определении среднего гармонического индекса себестоимости являются издержки производства текущего периода, а индекса
- 57. 7. Общие (сводные) индексы средних величин В экономико-статистическом анализе приходится сравнивать в динамике такие обобщающие характеристики
- 58. Индексы средних величин применяются при обобщении данных не по элементам, а по единицам совокупности. Например: цена
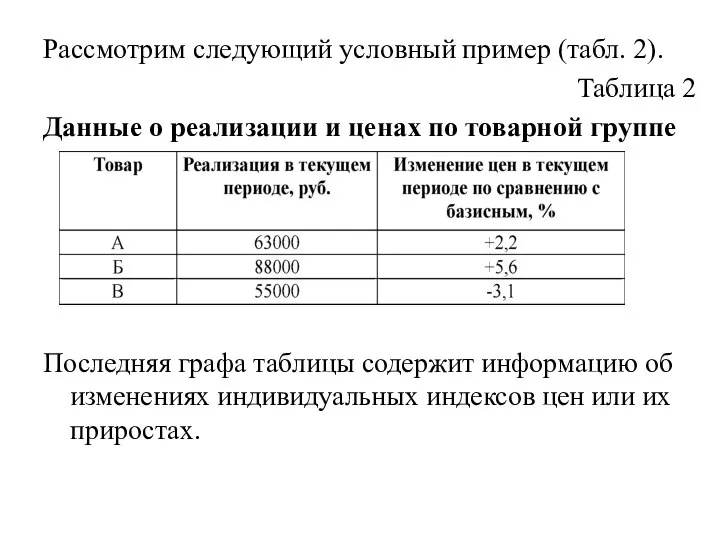
- 59. Рассмотрим следующий условный пример (табл. 2). Таблица 2 Данные о реализации и ценах по товарной группе
- 60. Рассчитаем значение сводного индекса Мы получили значение сводного индекса цен в средней гармонической форме, соответствующее сводному
- 61. Среднеарифметическая форма также может использоваться при расчете сводного индекса физического объема товарооборота. При этом производится замена
- 62. Таблица 3 Данные о реализации трех товаров в натуральном и стоимостном выражении Индивидуальные индексы физического объема
- 63. 7. Общие (сводные) индексы средних величин В экономико-статистическом анализе приходится сравнивать в динамике такие обобщающие характеристики
- 64. Индексы средних величин применяются при обобщении данных не по элементам, а по единицам совокупности. Например: цена
- 65. Данное выражение можно представить в виде мультипликативной модели: , где – доли (удельные веса) объемов продажи,
- 66. Такие индексы образуют индексную систему, которая для качественных показателей состоит из трех элементов: индексов переменного состава
- 67. где х1, х0 — средние признаки соответственно в текущем и базисном периодах; f1, f0 — веса
- 68. Индекс фиксированного состава IхФС характеризует изменение среднего уровня за счет изменения только индексируемой величины (соизмерители неизменны)
- 69. Индекс структурных сдвигов IхСЗ показывает изменение среднего уровня за счет изменений в структуре совокупности при неизменном
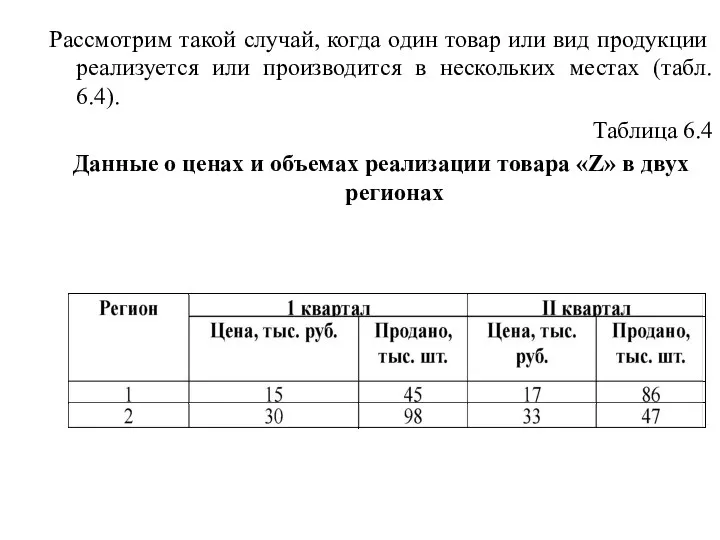
- 70. Рассмотрим такой случай, когда один товар или вид продукции реализуется или производится в нескольких местах (табл.
- 71. Проведем анализ изменения цен на данный товар. Из табл. 6.4 видно, что цена в каждом регионе
- 72. На динамике средней цены данного товара отразились структурные сдвиги в рассматриваемой совокупности. Оценить воздействие этого фактора
- 73. Последним в данной системе является индекс цен фиксированного состава, который не учитывает влияние структуры Полученное значение
- 74. Однако влияние на среднюю цену фактора структурных изменений оказалось сильнее и в итоге цена даже несколько
- 75. Абсолютные изменения средней цены в целом и по факторам определяются формулами: Очевидно, справедливо соотношение: .
- 76. 8. Индексный анализ территориальных различий Первый вариант расчета территориальных индексов заключается в том, что в качестве
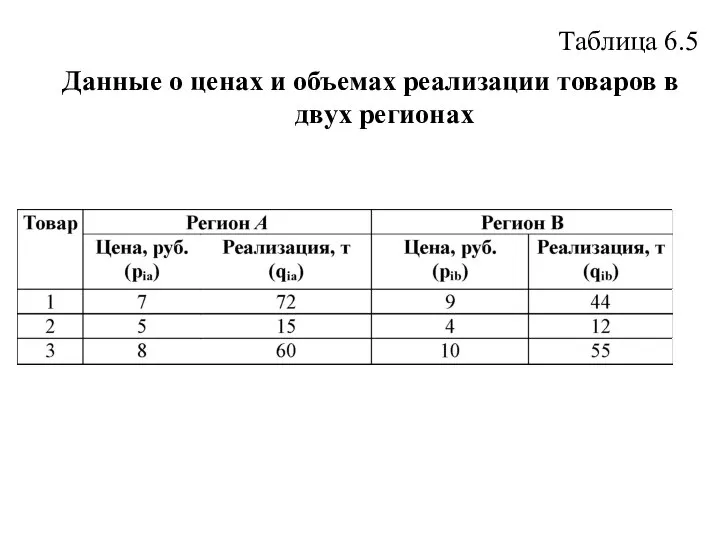
- 77. Таблица 6.5 Данные о ценах и объемах реализации товаров в двух регионах
- 78. Суммарные объемы реализации товаров по двум регионам соответственно составят 72+44=116; 15+12=27; 60+55=115. С учетом этих объемов
- 79. Этому выводу не противоречит и обратный индекс При расчете территориальных индексов данным способом в их формуле
- 80. Например, при сравнении уровней цен по двум районам области в качестве таких весов может выступать структура
- 81. Второй возможный способ расчета территориальных индексов учитывает соотношение весов на каждой из сравниваемых территорий. При этом
- 82. Рассчитаем средние цены товаров по данным табл. 6.5 С учетом рассчитанных средних цен вычислим индекс
- 83. Рассчитанный вторым способом территориальный индекс цен индекс физического объема реализации и индекс товарооборота будут взаимосвязаны между
- 84. 9. Индексы международного сопоставления Индекс ЭКШ где EKSB/A — индекс по формуле ЭКШ для страны В
- 86. Скачать презентацию
































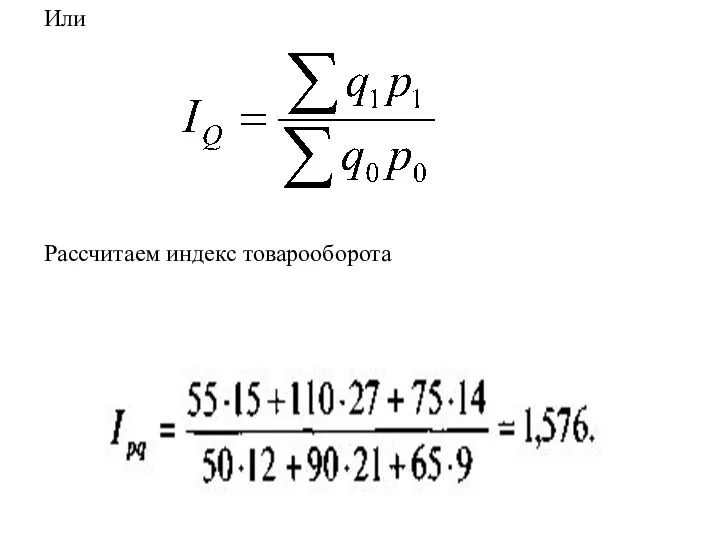






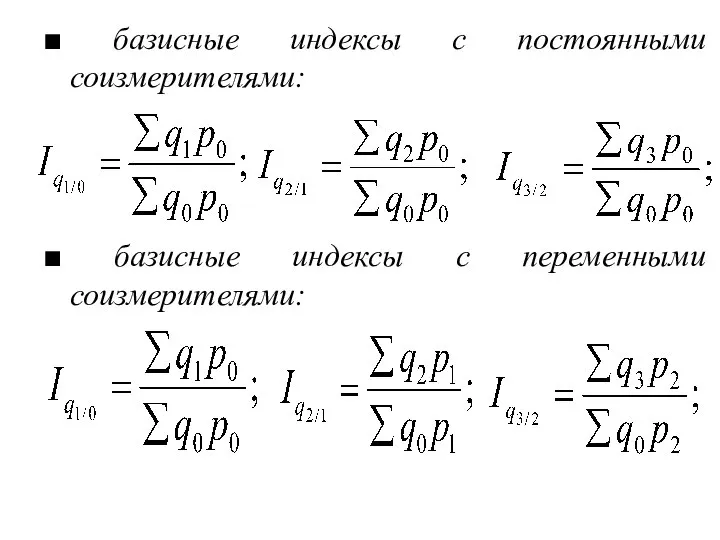





































 Экономическое (финансовое) обоснование сальдо операционных потоков
Экономическое (финансовое) обоснование сальдо операционных потоков Обзор общехозяйственной конъюнктуры развитой страны. Шаблон
Обзор общехозяйственной конъюнктуры развитой страны. Шаблон Место и роль бюджетно-налоговой политики в экономике с рациональными ожиданиями
Место и роль бюджетно-налоговой политики в экономике с рациональными ожиданиями Модель инновационного потенциала личности и группы
Модель инновационного потенциала личности и группы Макроэкономический спрос и предложение
Макроэкономический спрос и предложение Метод полного попарного сопоставления
Метод полного попарного сопоставления Оценка эффективности на предприятии
Оценка эффективности на предприятии Доходы и расходы семьи
Доходы и расходы семьи Предложения для резолюции по кризису
Предложения для резолюции по кризису Облікова політика підприємства (Лекція №3)
Облікова політика підприємства (Лекція №3) Предельные величины и эластичность в экономике
Предельные величины и эластичность в экономике Коллективный договор
Коллективный договор Логико-гносеологический и междисциплинарный анализ процесса формирования предмета экономической науки
Логико-гносеологический и междисциплинарный анализ процесса формирования предмета экономической науки Повышения эффективности использования трудовых ресурсов организации
Повышения эффективности использования трудовых ресурсов организации Общие положения по определению сметной стоимости строительства. Лекция 5
Общие положения по определению сметной стоимости строительства. Лекция 5 Износ и амортизация основных фондов
Износ и амортизация основных фондов Консорциум EEN - Россия: итоги деятельности Консорциума и его Региональных партнеров в 2017 году
Консорциум EEN - Россия: итоги деятельности Консорциума и его Региональных партнеров в 2017 году Региональное управление и территориальное планирование. Инструменты управления экономикой региона
Региональное управление и территориальное планирование. Инструменты управления экономикой региона Анализ основных показателей деятельности организации (на примере Могзонской дистанции пути)
Анализ основных показателей деятельности организации (на примере Могзонской дистанции пути) Становление рыночной экономики в современной России
Становление рыночной экономики в современной России Безграничность потребностей и ограниченность ресурсов. Проблема выбора
Безграничность потребностей и ограниченность ресурсов. Проблема выбора Спрос и предложение, 8 класс
Спрос и предложение, 8 класс Производство. Виды фирм
Производство. Виды фирм Экономическая деятельность. Экономические блага
Экономическая деятельность. Экономические блага Контекстная реклама. Точечное попадание в целевую аудиторию
Контекстная реклама. Точечное попадание в целевую аудиторию Издержки экономические и бухгалтерские, бухгалтерская и экономическая прибыль
Издержки экономические и бухгалтерские, бухгалтерская и экономическая прибыль Государственное регулирование экономики
Государственное регулирование экономики Метод группировки Подготовила: Клеутина С.А. Группа МЭ-092
Метод группировки Подготовила: Клеутина С.А. Группа МЭ-092