Динамика материальной точки

Динамика материальной точки (частицы)
1. Состояние частицы в классической механике. Механическое движение частицы. Принцип причинности.
2. Инерциальные системы отсчёта (ИСО). Первый закон Ньютона.
3. Сила. Инертная масса. Импульс. Второй закон Ньютона.
4. Уравнение движения частицы постоянной массы. Начальные условия. Связи. Прямая и обратная задачи механики.
5. Взаимодействие двух частиц. Третий закон Ньютона.
6. Силы упругости и трения. Законы Гука и Амонтона - Кулона. Формула Стокса.
7. Сила всемирного тяготения. Гравитационная (тяжелая) масса. Принцип эквивалентности.

Состояние частицы в классической
механике.
В классической механике состояние частицы определяется с помощью её радиус-вектора (t) и мгновенной скорости .
Механическое движение понимается как изменение во времени состояния частицы. Состояние частицы может быть задано только после выбора определённой системы отсчёта. Системы отсчета, построенные на основе тел, не имеющих ускорения называются инерциальными .

ПРИНЦИП ПРИЧИННОСТИ
Законы динамики выражают причинно-следственную связь между источником движения и характером этого движения (изменением состояния частицы). Принцип причинности играет очень важную роль во всей физике, поскольку выражает связь, детерминированность, обусловленность событий, протекающих последовательно во времени. Причина всегда предшествует во времени следствию.

Причиной изменения характера движения является сила.
Сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
Под действием сил тела либо изменяют
скорость движения, т.е. приобретают ускорения
( динамическое проявление сил ), либо
деформируются, т.е. изменяют свою форму и
размеры ( статическое проявление сил).
В системе СИ сила измеряется в ньютонах [Н].
1Н=1кг·м/с2

Законы Ньютона
Исаак Ньютон (1642 - 1727) – великий ученый, сделавший большой вклад в развитие физики и математики.
важнейшие работы:
закон всемирного тяготения, дифференциальное и интегральное исчисления, изобрел зеркальный телескоп

Первый закон Ньютона:
Всякая материальная точка сохраняет
состояние покоя или равномерного прямолиней-
ного движения до тех пор, пока воздействие со
стороны других тел не заставит её изменить
это состояние.
Стремление тела сохранять
состояние покоя или равномер-
ного прямолинейного движения
называется инертностью.
Первый закон Ньютона
называют законом инерции.

Механическое движение относительно, и его характер зависит от системы отсчёта. Первый закон Ньютона выполняется не во всякой системе отсчёта, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчёта.
Инерциальной системой отсчёта является такая система отсчёта, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется прямолинейно и равномерно (т.е. с постоянной скоростью).
Таким образом, первый закон Ньютона утверждает существование инерциальных систем отсчёта (ИСО).
В природе существует ИСО. Это гелиоцентрическая система: в центре – солнце, оси направлены на удаленные звезды, положение которых мало меняется в пространстве.

Система отсчёта, связанная с Землей, строго говоря, неинерциальная, однако эффекты, обусловленные её неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца) при решении многих задач малы, и в этих случаях её можно считать инерциальной.
Из приведённых выше примеров легко понять, что основным признаком инерциальной системы является отсутствие ускорения.

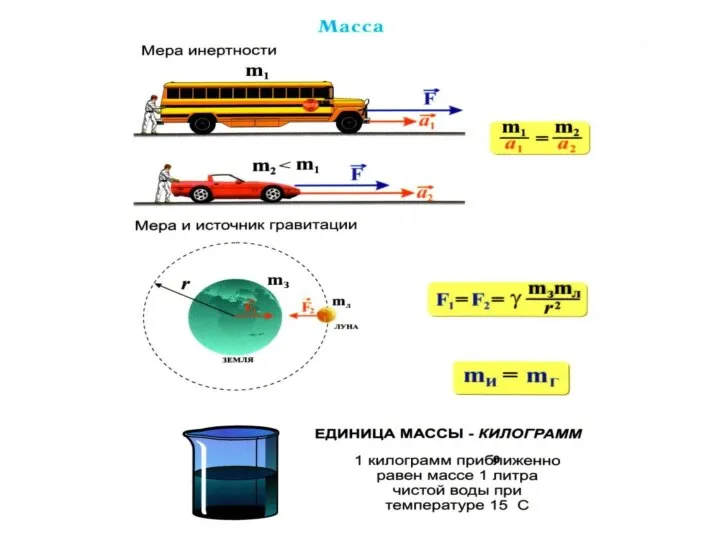
При одинаковых воздействиях различные тела
неодинаково изменяют скорость своего движения, т.е. приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойства самого тела (от его массы).
Масса тела – физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства.
Доказано, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10-12 их значения)
Масса – величина аддитивная (масса тела равна сумме масс частей, составляющих это тело).
Масса

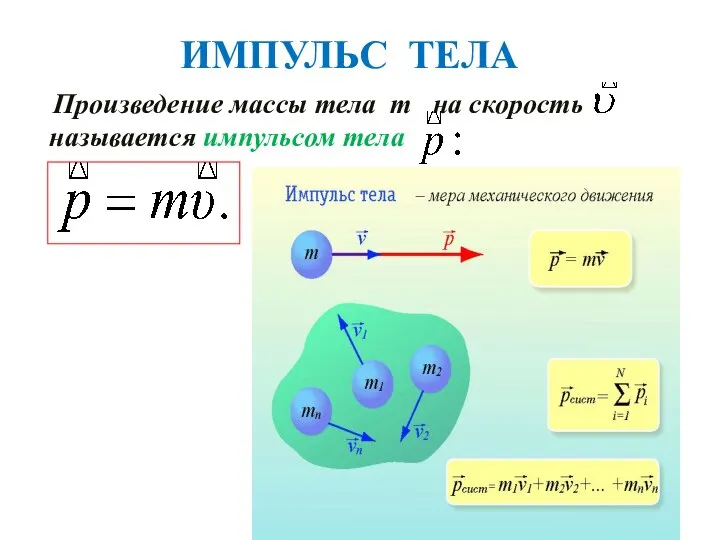
ИМПУЛЬС ТЕЛА
Произведение массы тела m на скорость
называется импульсом тела

Второй закон Ньютона
Согласно второму закону Ньютона, в инерциальной системе отсчета первая производная импульса частицы по времени t равна полной (суммарной) силе , действующей на частицу:
где полная сила есть векторная сумма всех сил, действующих на частицу. В системе СИ масса m измеряется в килограммах, а сила – в ньютонах.

Выражение второго закона через ускорение a :
т. к.
то
но
тогда
2-ой закон
Ньютона
(уравнение движения частицы постоянной массы)
Масса, умноженная на ускорение, равна
действующей силе.
Второй закон Ньютона
можно записать в другом
виде: и это
читается:
изменение импульса равно импульсу
силы.

Уравнение движения частицы постоянной массы. При заданной силе , неизвестной функцией времени является радиус-вектор частицы (обыкновенное дифференциальное уравнение второго порядка по времени)
Для однозначного нахождения решения дифференциального уравнения необходимо задать не только действующую силу, но и два начальных условия.

Третий закон Ньютона
Взаимодействие между материальными точками (телами) в инерциальной системе отсчёта определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и
действуют вдоль прямой,
соединяющей эти точки:

Всякое действие вызывает равное по величине противодействие
3-й Закон Ньютона в общем случае является универсальным законом взаимодействий:
F21
F12
Подчеркнем, что силы, связанные по 3 закону Ньютона, приложены к различным телам и, следовательно, никогда не могут начинаться в одной точке и компенсировать друг друга

силы в механике
В настоящее время в физике, различают четыре типа сил или взаимодействий:
гравитационные;
электромагнитные;
сильные (ответственные за связь частиц в ядрах)
слабые (ответственные за распад частиц)

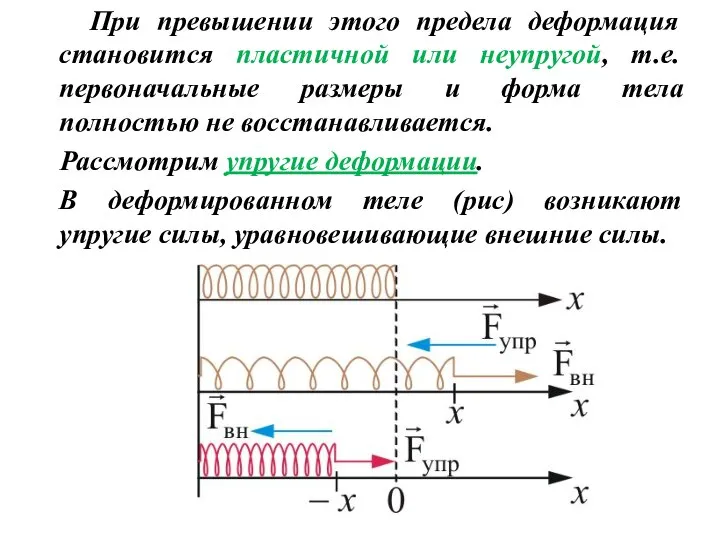
Силы упругости
Электромагнитные силы, действующие между молекулами и атомами, проявляют себя как упругие силы и силы трения.
Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, которая называется пределом упругости.

При превышении этого предела деформация становится пластичной или неупругой, т.е. первоначальные размеры и форма тела полностью не восстанавливается.
Рассмотрим упругие деформации.
В деформированном теле (рис) возникают упругие силы, уравновешивающие внешние силы.

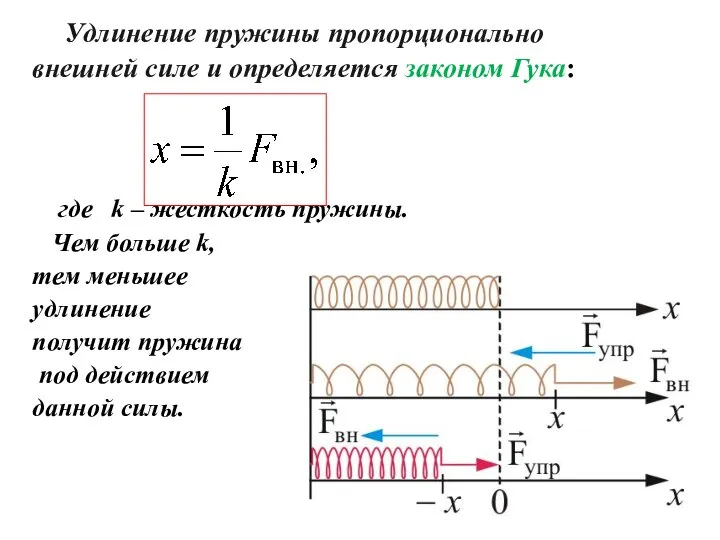
Удлинение пружины пропорционально
внешней силе и определяется законом Гука:
где k – жесткость пружины.
Чем больше k,
тем меньшее
удлинение
получит пружина
под действием
данной силы.

Роберт Гук (1635 – 1703)-
знаменитый английский физик,
сделавший множество
изобретений и открытий в области
механики, термодинамики,
положил начало физической оптике.

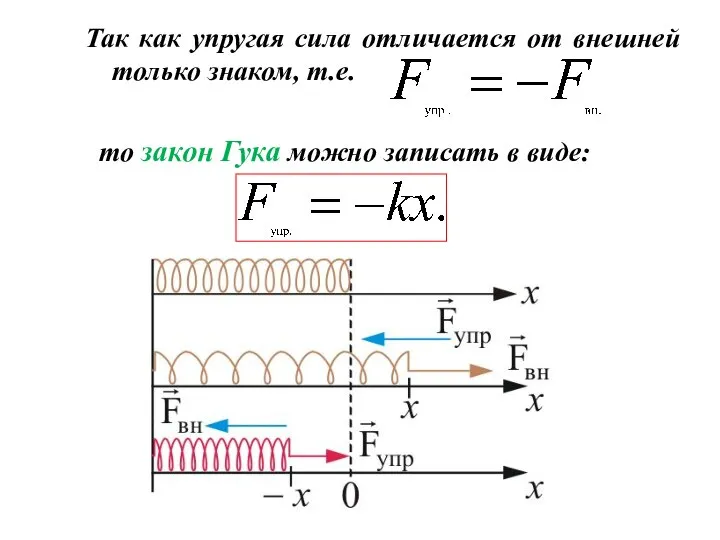
Так как упругая сила отличается от внешней только знаком, т.е.
то закон Гука можно записать в виде:

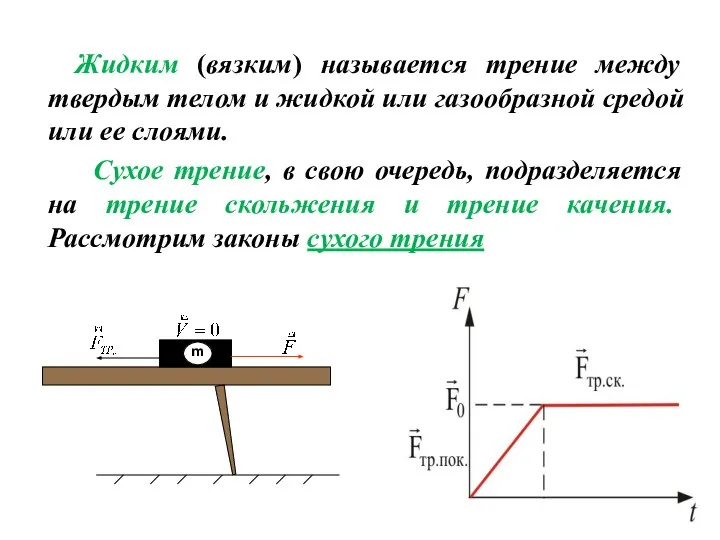
Cилы трения
Введем классификацию сил трения.
Трение подразделяется на внешнее и внутреннее.
Внешнее трение возникает при относительном перемещении двух соприкасающихся твердых тел (трение скольжения или трение покоя).
Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ).
Различают сухое и жидкое (или вязкое) трение.

Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями.
Сухое трение, в свою очередь, подразделяется на трение скольжения и трение качения. Рассмотрим законы сухого трения

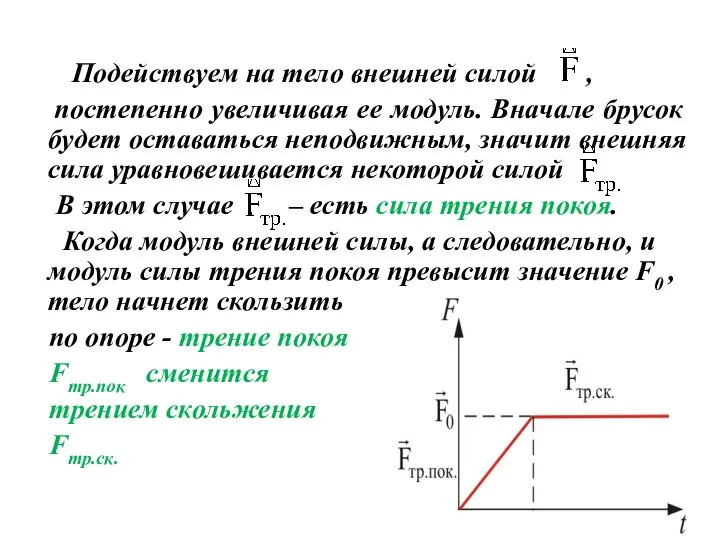
Подействуем на тело внешней силой ,
постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным, значит внешняя сила уравновешивается некоторой силой
В этом случае – есть сила трения покоя.
Когда модуль внешней силы, а следовательно, и модуль силы трения покоя превысит значение F0 , тело начнет скользить
по опоре - трение покоя
Fтр.пок сменится
трением скольжения
Fтр.ск.

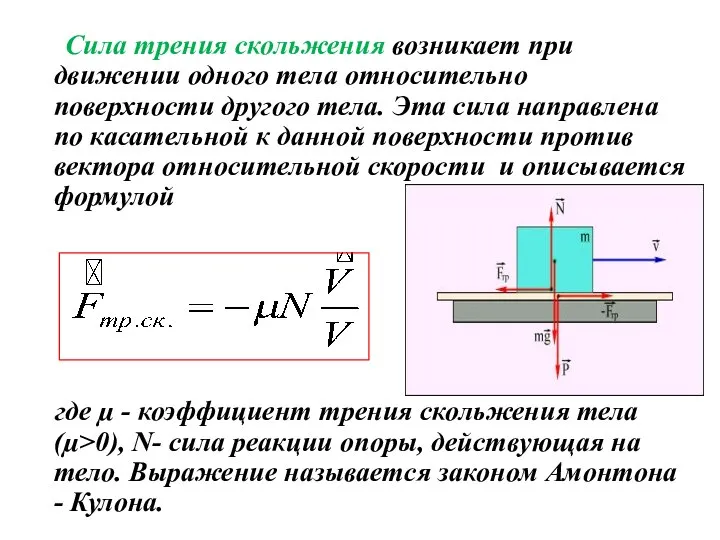
Сила трения скольжения возникает при движении одного тела относительно поверхности другого тела. Эта сила направлена по касательной к данной поверхности против вектора относительной скорости и описывается формулой
где µ - коэффициент трения скольжения тела (µ>0), N- сила реакции опоры, действующая на тело. Выражение называется законом Амонтона - Кулона.

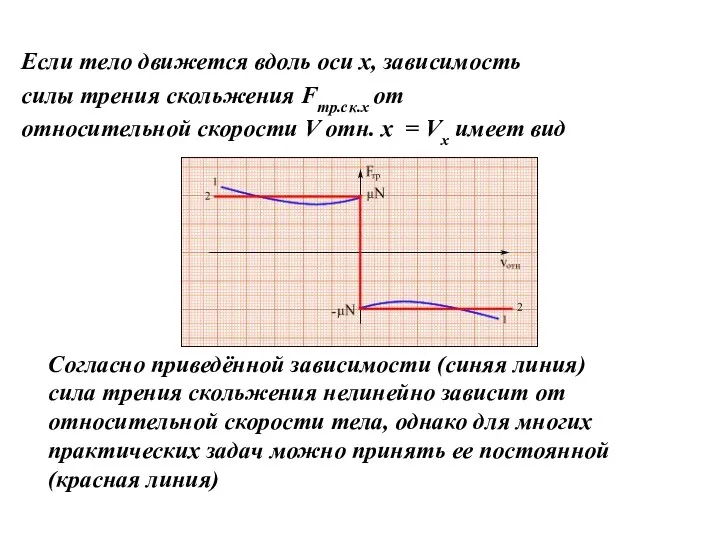
Если тело движется вдоль оси х, зависимость
силы трения скольжения Fтр.ск.х от
относительной скорости V отн. х = Vx имеет вид
Согласно приведённой зависимости (синяя линия) сила трения скольжения нелинейно зависит от относительной скорости тела, однако для многих практических задач можно принять ее постоянной (красная линия)

Установлено, что максимальная сила трения
покоя не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю силы нормального давления N
μ0 – коэффициент трения покоя – зависит от природы и состояния трущихся поверхностей.
Аналогично и для силы трения скольжения

В случае относительно медленного движения тела в газовой или жидкой среде на него действует сила вязкого трения:
где V - скорость тела и b >0 – коэффициент, зависящий от свойств среды и тела. Для гладкого шарика радиусом r справедлива формула Стокса
b = 6πηr - сила Стокса
где η - вязкость среды. В области больших скоростей следует учитывать силу сопротивления среды, величина которой пропорциональна квадрату скорости и площади поперечного сечения тела.

Сила всемирного тяготения
Основой для формулировки закона всемирного тяготения Ньютоном послужили эмпирические законы Кеплера, полученные путём обобщения многолетних наблюдений за движением планет Солнечной системы. Кеплер

Согласно Ньютону сила гравитационного притяжения двух частиц, находящихся на расстоянии r друг от друга, описывается формулой
где - гравитационная постоянная.

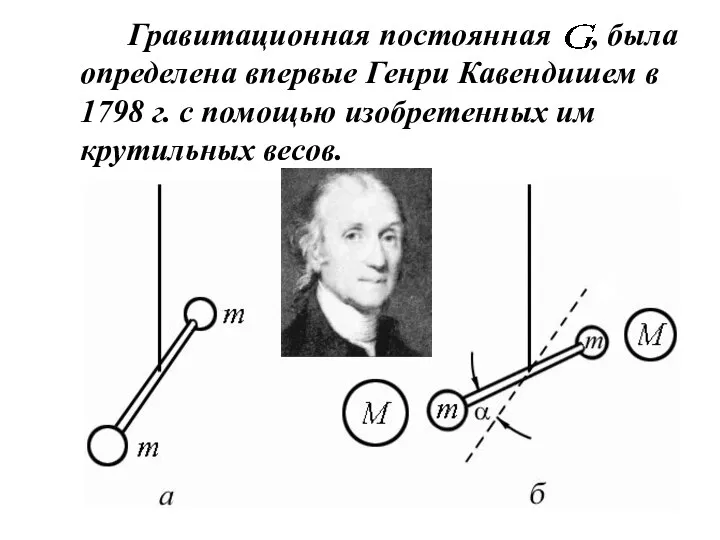
Гравитационная постоянная , была определена впервые Генри Кавендишем в 1798 г. с помощью изобретенных им крутильных весов.