Неравновесные состояния и необратимые процессы. Броуновское движение

СВОЙСТВА НЕОБРАТИМЫХ ПРОЦЕССОВ
- существенно нелинейная зависимость от параметров состояния;
- большой уровень флуктуаций;
- сильная зависимость от предыстории;
- существенное влияние других необратимых процессов;
- плохая предсказуемость.

ОПИСАНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Примеры дифференциальных уравнений:
- второй закон Ньютона;
- уравнения Максвелла;
- уравнения гидродинамики;
- описание диффузии и теплопроводности;
- описание броуновского движения;
- уравнение Шредингера;
- уравнение радиоактивного распада.

ОПИСАНИЕ ДЕТЕРМИНИРОВАННЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Метод описания основан на решении дифференциального уравнения:
(1)
с начальным условием
(2)

ОПИСАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
Уравнение Фоккера-Планка:
(3)
с начальным условием
(4)

ПРОСТОЙ ПРИМЕР
Решить уравнение
(5)
с начальным условием
(6)
Решение
(7)

ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ
Линейное интегральное уравнение
(8)
Примеры ядер интегрального уравнения
1) (9)
2) (10)
3) (11)

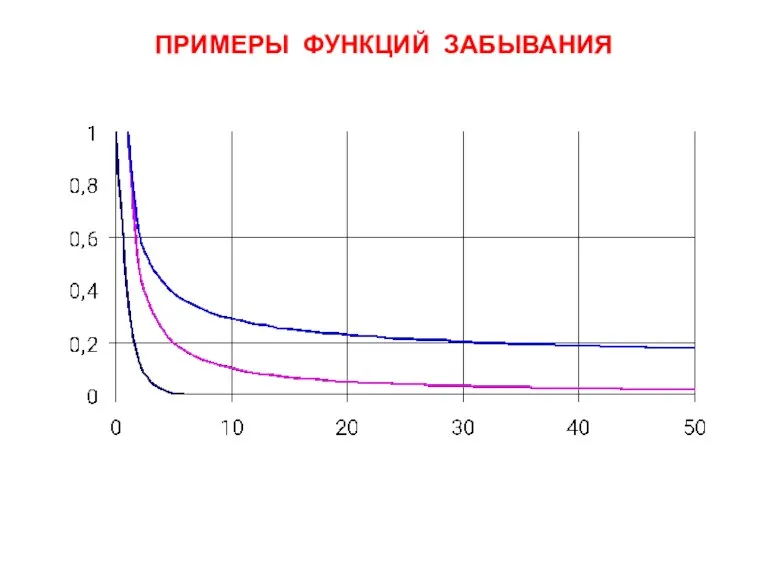
ПРИМЕРЫ ФУНКЦИЙ ЗАБЫВАНИЯ

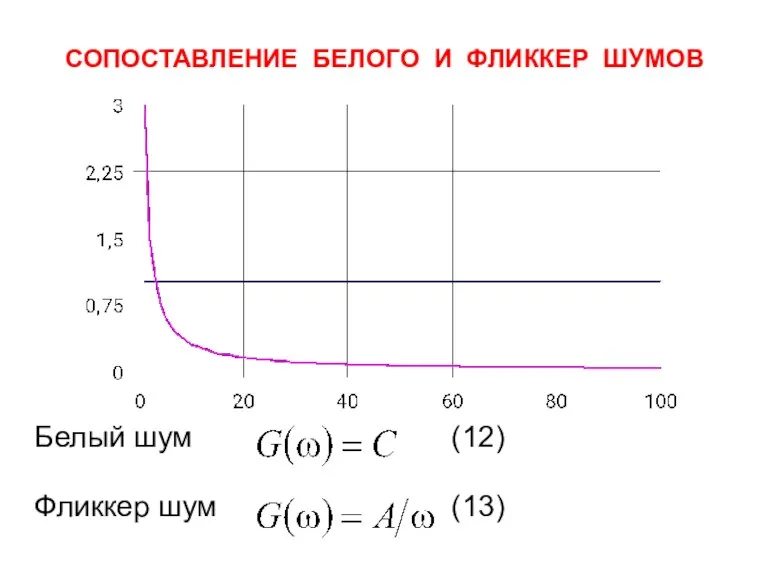
СОПОСТАВЛЕНИЕ БЕЛОГО И ФЛИККЕР ШУМОВ
Белый шум (12)
Фликкер шум (13)

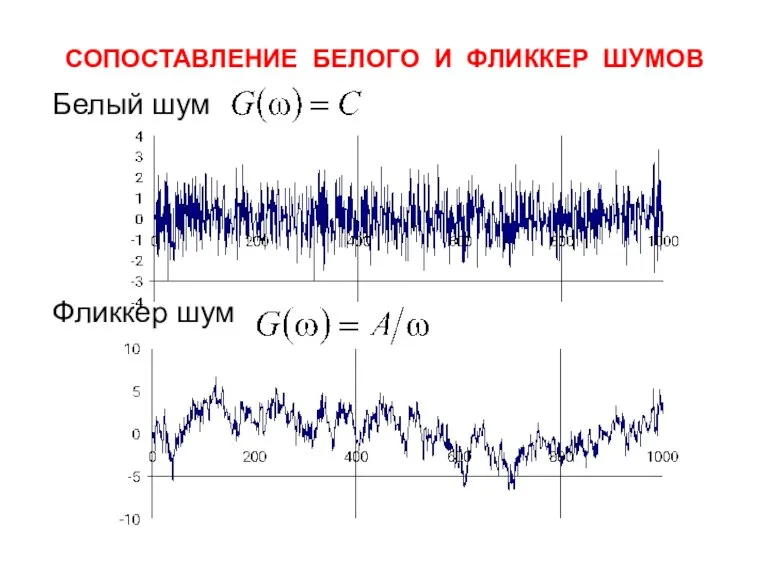
СОПОСТАВЛЕНИЕ БЕЛОГО И ФЛИККЕР ШУМОВ
Белый шум
Фликкер шум

БРОУНОВСКОЕ ДВИЖЕНИЕ
Уравнение движения частицы в вязкой среде
(14)
где (15)
Спектральная плотность шума (16)
Спектральная плотность флуктуаций скорости (17)
где , .

БРОУНОВСКОЕ ДВИЖЕНИЕ ШАРООБРАЗНОЙ ЧАСТИЦЫ В ВЯЗКОЙ СРЕДЕ
Сила вязкого трения
(18)
Спектральная плотность флуктуаций скорости
(19)

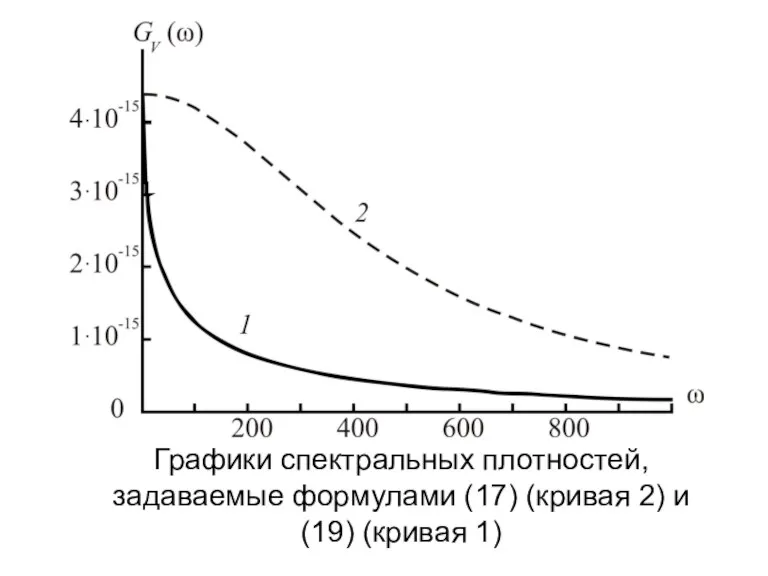
Графики спектральных плотностей, задаваемые формулами (17) (кривая 2) и (19) (кривая 1)

НЕМАРКОВСКИЕ ПРОЦЕССЫ
Примеры немарковских процессов, наблюдаемых в природе и технике:
- фликкер-шум, наблюдаемый в процессах, имеющих различную физическую природу;
- флуктуации кинетических коэффициентов (например, флуктуации коэффициентов диффузии, вязкости и теплопроводности);
- результат интегрирования марковского случайного процесса, в частности, координата броуновской частицы, вычисляемая как интеграл от её скорости;

- отклик динамической системы при воздействии на неё марковского случайного процесса;
- результат измерений с помощью динамической измерительной системы;
- радиотехнические сигналы при их амплитудной и фазовой модуляции совокупностью детерминированных и случайных процессов;
- результат нахождения скользящего среднего от процесса с независимыми значениями;
- результат фильтрации (как временной, так и частотной) марковского случайного процесса.

СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнение Ито
, (20)
где - процесс с независимыми приращениями.
Интегральное представление (21)
Уравнение для характеристической функции
(22)

Решение уравнения
(23)
Для винеровского процесса
. (24)
Для пуассоновского процесса
(25)

НЕМАРКОВСКИЙ ПРОЦЕСС, ЗАДАВАЕМЫЙ ЛИНЕЙНЫМ ИНТЕГРАЛЬНЫМ ПРЕОБРАЗОВАНИЕМ
Связь плотности термодинамических потоков и термодинамических сил
. (26)
При
(27)
выражение (26) приобретает вид алгебраического равенства
. (28)

Интегральное преобразование
(29)
Характеристическая функция
.(30)
Случаи винеровского и пуассоновского процессов
, (31)
.
.(32)

ФЛИККЕР-ШУМ
Если ядро интегрального преобразования
, (33)
то
(34)
Спектр шума
(35)

НЕОБРАТИМЫЕ НЕМАРКОВСКИЕ ПРОЦЕССЫ
В рамках теории немарковских процессов описаны:
- броуновское движение;
- диффузия;
- теплопроводность;
- тепловое излучение;
- люминесценция;
- реология;
- флуктуации кинетических коэффициентов.

НЕМАРКОВСКИЙ ОСЦИЛЛЯТОР
Уравнение для осциллятора
(36)
Спектральная плотность флуктуаций координаты
(37)
Спектральная плотность для классического осциллятора
(38)

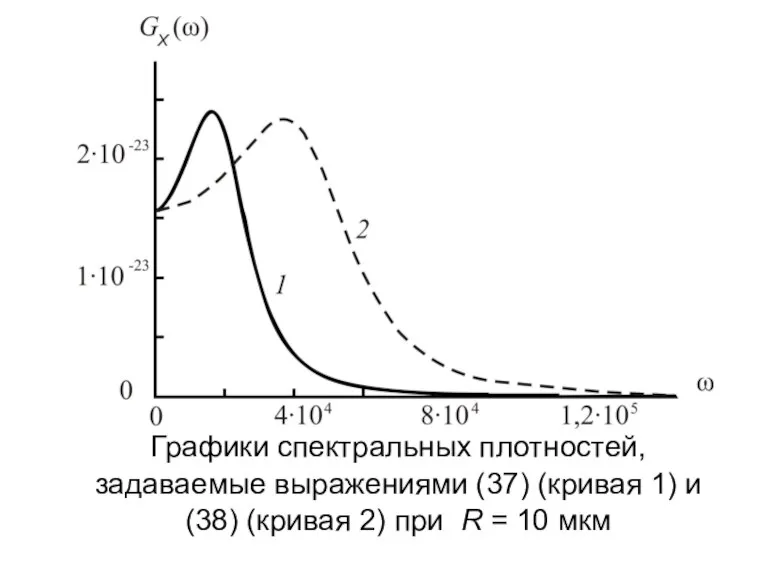
Графики спектральных плотностей, задаваемые выражениями (37) (кривая 1) и (38) (кривая 2) при R = 10 мкм

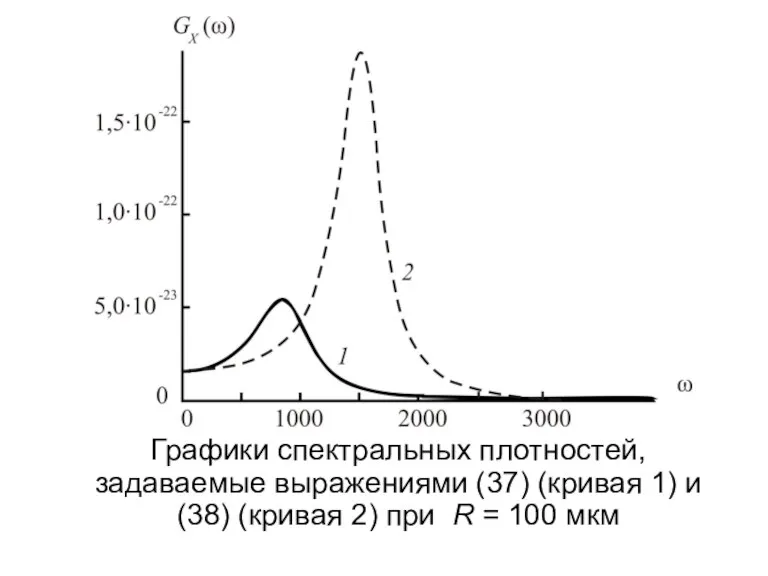
Графики спектральных плотностей, задаваемые выражениями (37) (кривая 1) и (38) (кривая 2) при R = 100 мкм

ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ НЕРАВНОВЕСНОСТИ СОСТОЯНИЯ
Формула Найквиста
(39)
Мера Кульбака
(40)
где
(41)

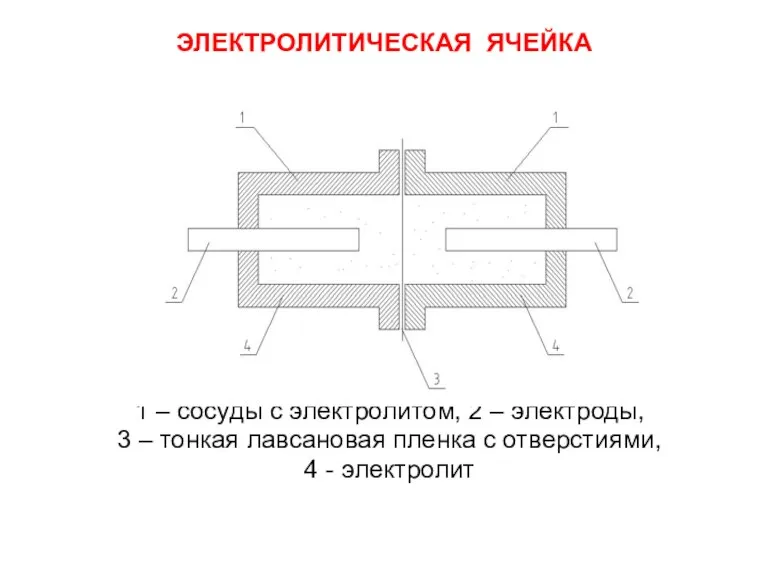
ЭЛЕКТРОЛИТИЧЕСКАЯ ЯЧЕЙКА
1 – сосуды с электролитом, 2 – электроды,
3 – тонкая лавсановая пленка с отверстиями,
4 - электролит

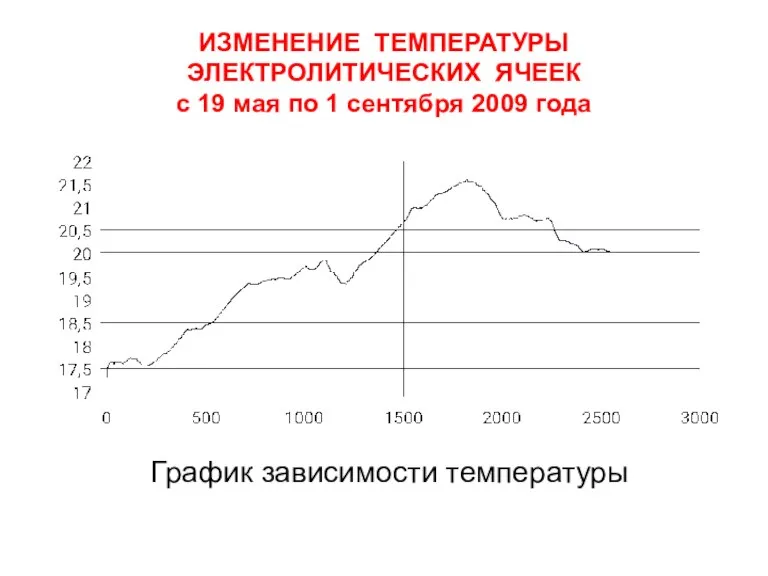
ИЗМЕНЕНИЕ ТЕМПЕРАТУРЫ ЭЛЕКТРОЛИТИЧЕСКИХ ЯЧЕЕК
с 19 мая по 1 сентября 2009 года
График зависимости температуры

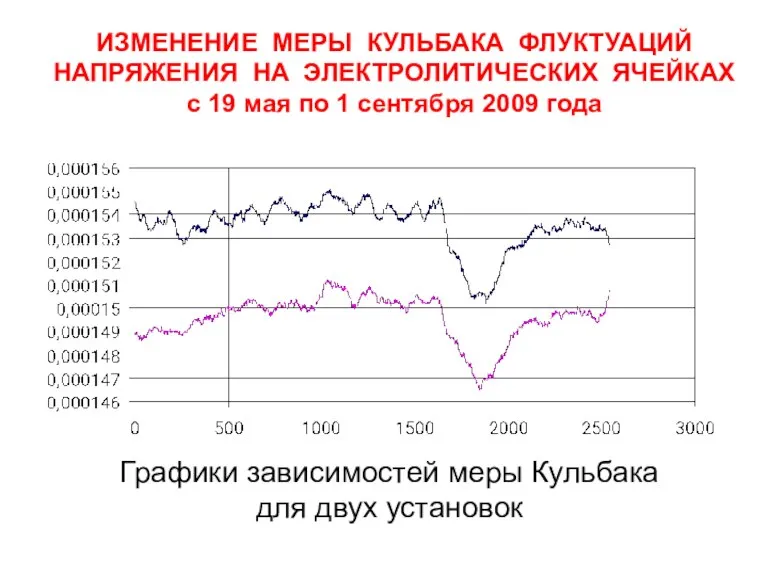
ИЗМЕНЕНИЕ МЕРЫ КУЛЬБАКА ФЛУКТУАЦИЙ НАПРЯЖЕНИЯ НА ЭЛЕКТРОЛИТИЧЕСКИХ ЯЧЕЙКАХ
с 19 мая по 1 сентября 2009 года
Графики зависимостей меры Кульбака
для двух установок