Содержание
- 2. Navigační metody Srovnávací navigace (orientace) Navigace výpočtem Radionavigace Spojování navigačních metod
- 3. Země a síí myšlených čar Na pólech je Země zploštělá V rovníkové oblasti má průměr 6378
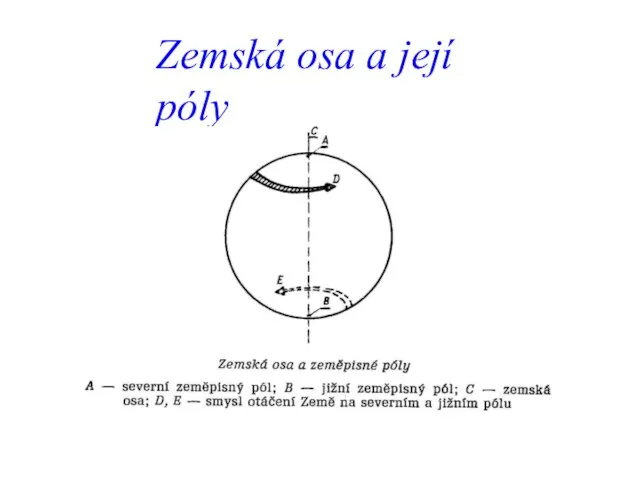
- 4. Zemská osa a její póly
- 5. Síí myšlených čar Zemská osa – myšlená přímka kolmá k rovníku, kolem které se Země otáčí
- 6. Poledník a rovník
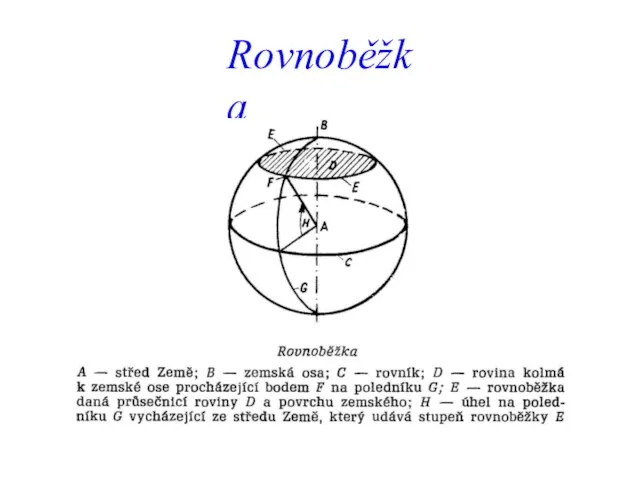
- 7. Rovnoběžka
- 8. Udávání poloh Polohou rozumíme bod, nad kterým se v daném okamžiku nacházíme Udávání polohy názvem místa,
- 9. Udávání poloh
- 10. Velká a malá kružnice a) Velká kružnice – průsečnice roviny s povrchem, procházející středem Země –
- 11. Velká a malá kružnice b) Malá kružnice – průsečnice roviny s povrchem, neprocházející středem Země –
- 12. Loxodroma a ortodroma c) Loxodroma - křivka na povrchu Zeměkoule, která protíná všechny poledníky pod stejným
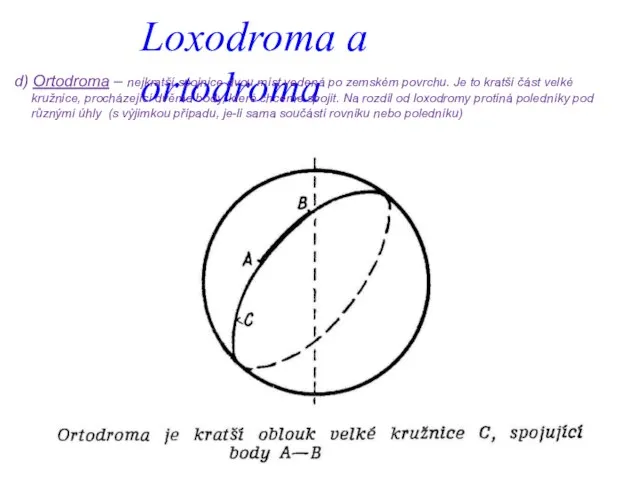
- 13. Loxodroma a ortodroma d) Ortodroma – nejkratší spojnice dvou míst vedená po zemském povrchu. Je to
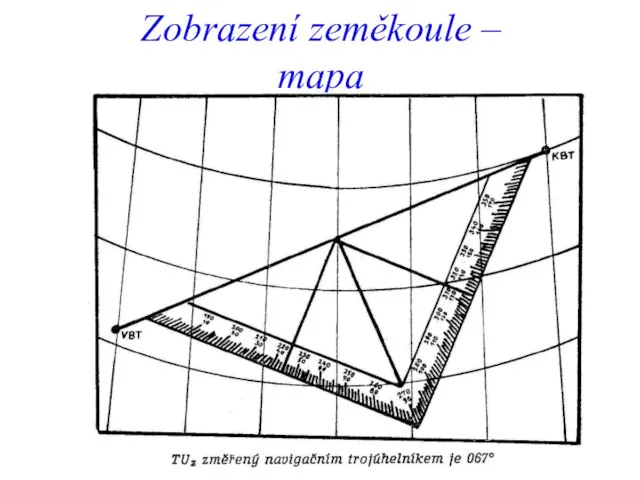
- 14. Zobrazení zeměkoule – mapa Povrch Země Topografická plocha: Skutečný, holý povrch Země bez objektů (se všemi
- 15. Zobrazení zeměkoule – mapa Mapa a její zkreslení Mapa je zmenšený rovinný obraz zemského povrchu. Povrch
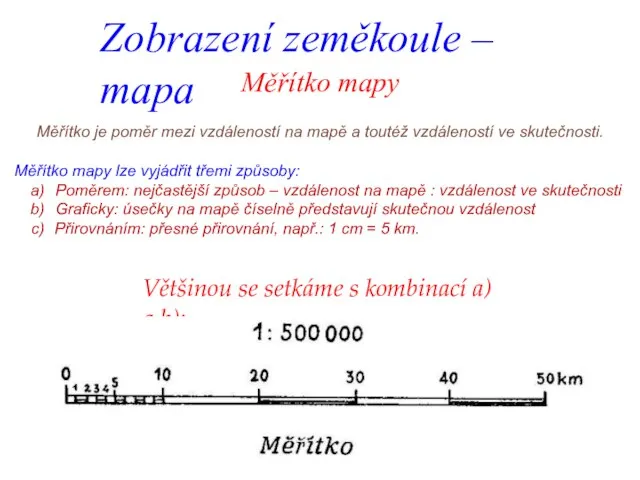
- 16. Zobrazení zeměkoule – mapa Měřítko mapy Měřítko je poměr mezi vzdáleností na mapě a toutéž vzdáleností
- 17. Zobrazení zeměkoule – mapa Měření vzdáleností na mapě Přepočtem: podle měřítka; např. na mapě 1:500 000
- 18. Zobrazení zeměkoule – mapa Měření úhlů na mapách Toto je jedním ze základních navigačních úkonů. Nejčastěji
- 19. Zobrazení zeměkoule – mapa Měření úhlů na mapách
- 20. Zobrazení zeměkoule – mapa Letecká mapa ICAO – 1:500 000 (Gauss-Krügerova projekce) Je to příčná válcová
- 21. Navigace výpočtem Základní navigační přístroje: kompas, rychloměr a hodinky. Tuto metodu používají hlavně motoroví piloti. Kompas:
- 22. Navigace výpočtem Navigační pojmy, prvky, zkratky Výchozí bod tratě – VBT – bod odletu: bod, ze
- 23. Navigace výpočtem pokračujeme: Úhel snosu – US – úhel mezi osou letadla (kursovou přímkou ) a
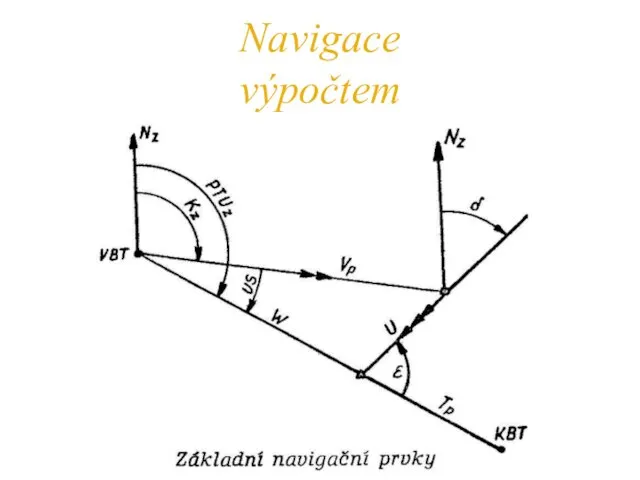
- 24. Navigace výpočtem základní navigační prvky
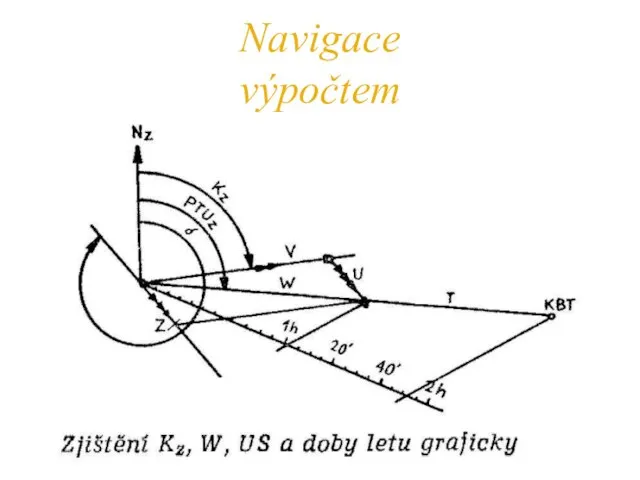
- 25. Navigace výpočtem grafické řešení navigační úlohy Pracujeme se třemi skupinami navigačních prvků: vektor pravé vzdušné rychlosti,
- 26. Navigace výpočtem navigační trojúhelník 150 km/hod, vítr je Příklad: plánovaný Tuz je 095°, vzdálenost mezi VBT
- 27. Navigace výpočtem navigační trojúhelník
- 28. Zemský magnetizmus Magnetická deklinace Polohy zemských magnetických pólů nejsou shodné s póly zeměpisnými. Dokonce jsou od
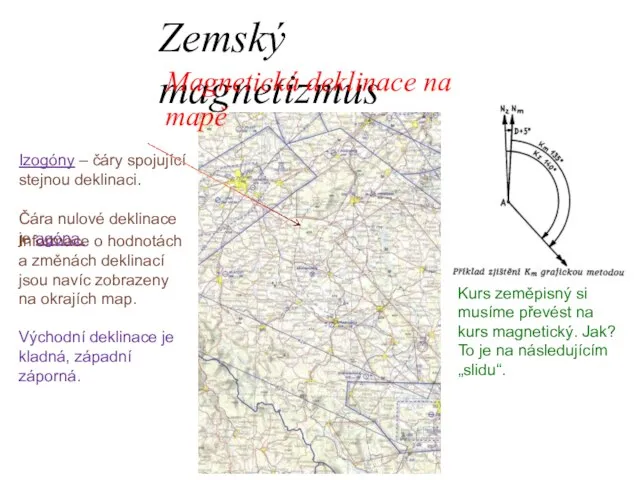
- 29. Zemský magnetizmus Magnetická deklinace na mapě Izogóny – čáry spojující stejnou deklinaci. Čára nulové deklinace je
- 30. Zemský magnetizmus Magnetická deklinace na mapě Převod provádíme prakticky výlučně matematicky: je-li deklinace kladná, je Km
- 31. Zemský magnetizmus Deviace kompasu Letecký kompas neukazuje nikdy přesně. Jeho hodnoty jsou ovlivněny magnetizmem letadla, který
- 32. Trochu zeměpisu
- 34. Скачать презентацию






















 Простые механизмы. Рычаг
Простые механизмы. Рычаг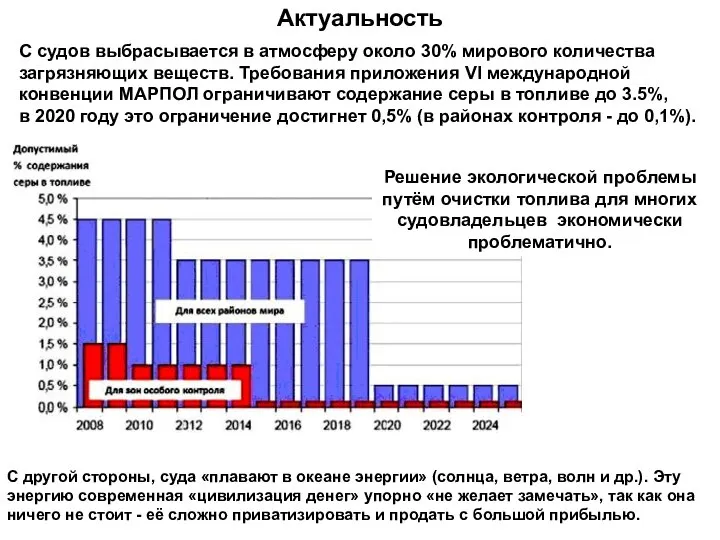 Поиск эффективных способов преобразования энергии морских волн в энергию поступательного движения судна
Поиск эффективных способов преобразования энергии морских волн в энергию поступательного движения судна Škoda Octavia. Кузов. Оборудование кузова
Škoda Octavia. Кузов. Оборудование кузова Открытия Ломоносова в области физики
Открытия Ломоносова в области физики Электронное пособие по физике для изучения законов постоянного тока
Электронное пособие по физике для изучения законов постоянного тока Лабораторная работа. Изучение устройства и принципа работы термодымовой камеры КТД-100
Лабораторная работа. Изучение устройства и принципа работы термодымовой камеры КТД-100 Презентация на тему Электрическая цепь и её составные части
Презентация на тему Электрическая цепь и её составные части  Механические колебания и волны. Звук
Механические колебания и волны. Звук Экспериментальные работы ОГЭ - 2020
Экспериментальные работы ОГЭ - 2020 Презентация на тему Дифракционные решетки
Презентация на тему Дифракционные решетки  Физики, внесшие вклад в развитие науки и техники в годы Великой Отечественной войны
Физики, внесшие вклад в развитие науки и техники в годы Великой Отечественной войны Урок физики
Урок физики Автозвук на примере понятия звуковой волны
Автозвук на примере понятия звуковой волны Вывод формулы Резерфорда для вероятности обратного рассеяния альфа-частиц. АФ1.A
Вывод формулы Резерфорда для вероятности обратного рассеяния альфа-частиц. АФ1.A О, физика – наука из наук!
О, физика – наука из наук! Катушка Индуктивности
Катушка Индуктивности Силы, действующие на поезд. Теория электрической тяги
Силы, действующие на поезд. Теория электрической тяги Определение остаточных внутренних сил при разгрузке статически неопределимой балки
Определение остаточных внутренних сил при разгрузке статически неопределимой балки Подвеска. Техническое обслуживание, ремонт и эксплуатация автомобильного транспорта
Подвеска. Техническое обслуживание, ремонт и эксплуатация автомобильного транспорта Кинематика цепной передачи
Кинематика цепной передачи Презентация (1)
Презентация (1) Свободное падение тел_ Движение с ускорением свободного падения
Свободное падение тел_ Движение с ускорением свободного падения Механические передачи. Виды передач. Расчет передаточных отношений
Механические передачи. Виды передач. Расчет передаточных отношений ППШ
ППШ Сила трения
Сила трения Экспериментальные методы регистрации заряженных частиц
Экспериментальные методы регистрации заряженных частиц Сила упругости. Закон Гука
Сила упругости. Закон Гука Тематический состав ВсОШ по физике для 10-ого класса
Тематический состав ВсОШ по физике для 10-ого класса