Содержание
- 2. Геодезическая основа разбивочных работ. Элементы геодезических разбивочных работ. Способы разбивки основных осей объекта. «Содержание»
- 3. Геодезическая основа разбивочных работ. Под разбивкой сооружений (перенесением проекта в натуру) —понимают комплекс геодезических работ по
- 4. При разбивочных работах на местности строят углы, откладывают отрезки линий (в плане и по высоте), т.
- 5. Строительная сетка Представляет сеть квадратов или прямоугольников, вершины которых закреплены на местности геодезическими знаками. Последние должны
- 6. Характерной особенностью строительной сетки как инженерно-геодезической сети является расположение пунктов, образующих сетку квадратов или прямоугольников, стороны
- 7. Строительная сетка предназначена: 1) для выноса в натуру основных осей сооружений и производства разбивочных работ; 2)
- 8. В зависимости от назначения строительной сетки и типа строящегося объекта длину стороны квадрата или прямоугольника сетки
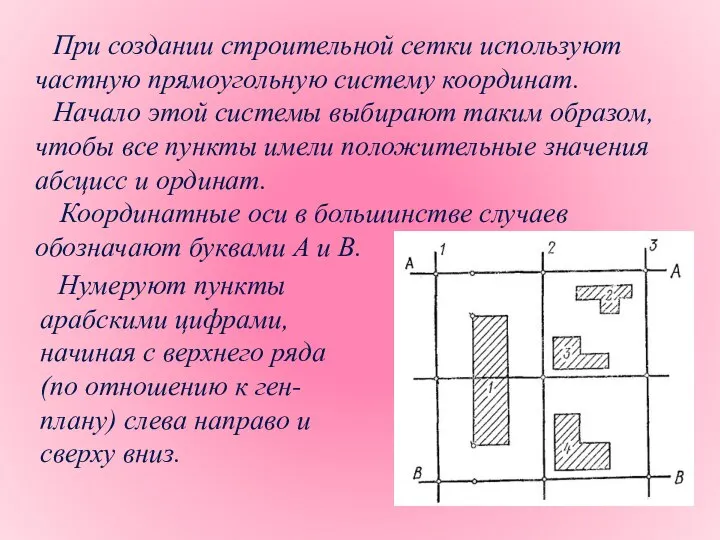
- 9. При создании строительной сетки используют частную прямоугольную систему координат. Начало этой системы выбирают таким образом, чтобы
- 10. Требования к точности строительных сеток : а) погрешности во взаимном положении смежных пунктов строительной сетки в
- 11. б) прямые углы строительной сетки должны быть построены с точностью порядка 20 ′′ ; в) погрешности
- 12. 2. Элементы геодезических разбивочных работ. Элементами геодезических разбивочных работ принято считать проектные углы, отрезки, точки с
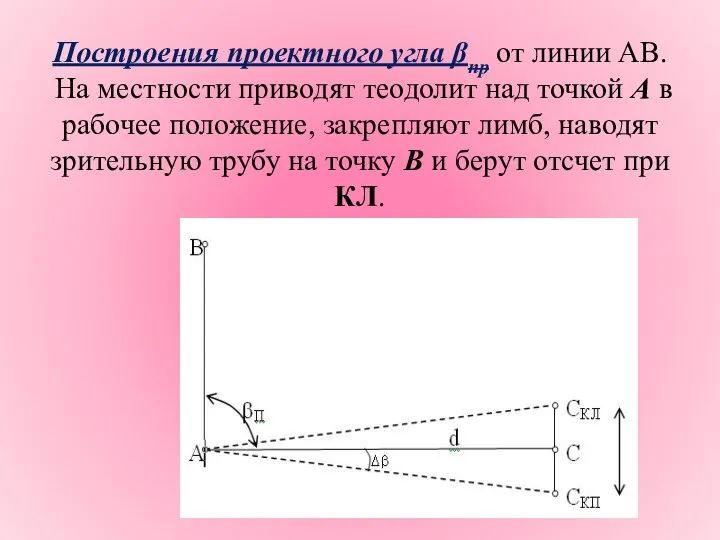
- 13. Построения проектного угла βпр от линии АВ. На местности приводят теодолит над точкой А в рабочее
- 14. Затем к этому отсчету прибавляют значение проектного угла, если угол откладывают по ходу часовой стрелки (если
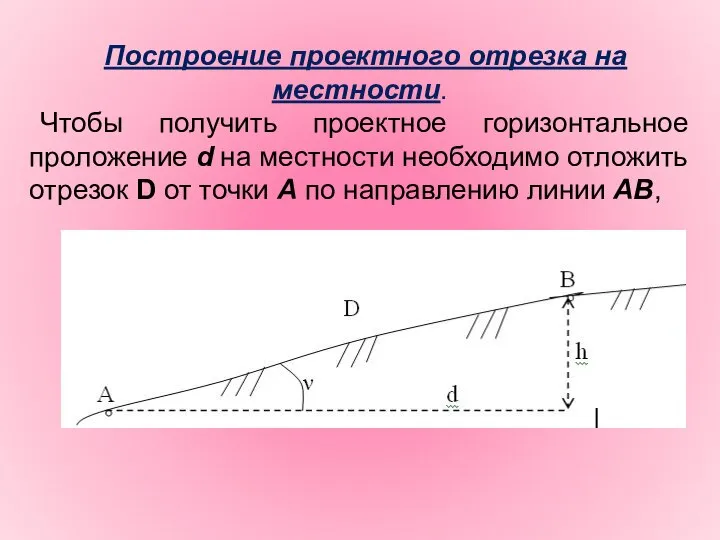
- 15. Построение проектного отрезка на местности. Чтобы получить проектное горизонтальное проложение d на местности необходимо отложить отрезок
- 16. Длина отрезка вычисляется по формуле: D = d + δDk + δDt + δDv , где
- 17. Вынос в натуру проектной высоты. Вынос в натуру проектной высоты Нпр осуществляют от ближайшего репера с
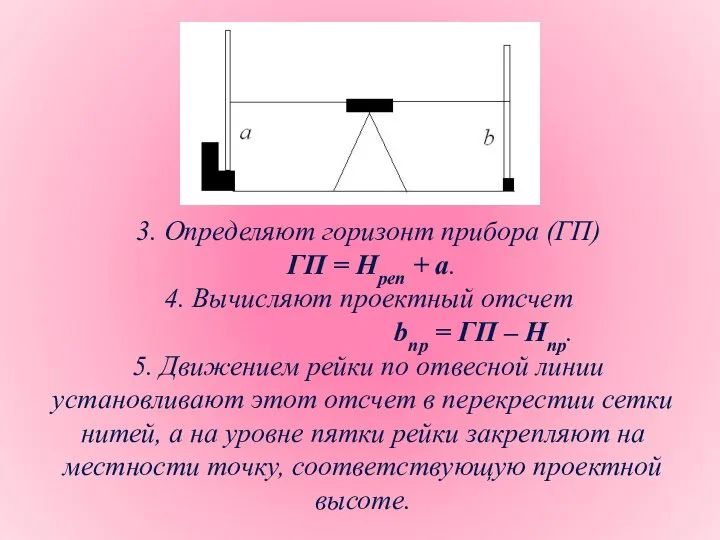
- 18. 3. Определяют горизонт прибора (ГП) ГП = Нреп + а. 4. Вычисляют проектный отсчет bпр =
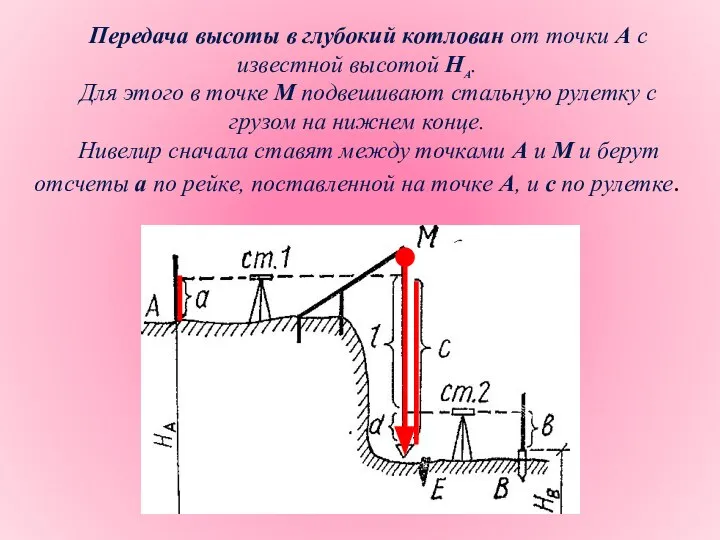
- 19. Передача высоты в глубокий котлован от точки А с известной высотой На. Для этого в точке
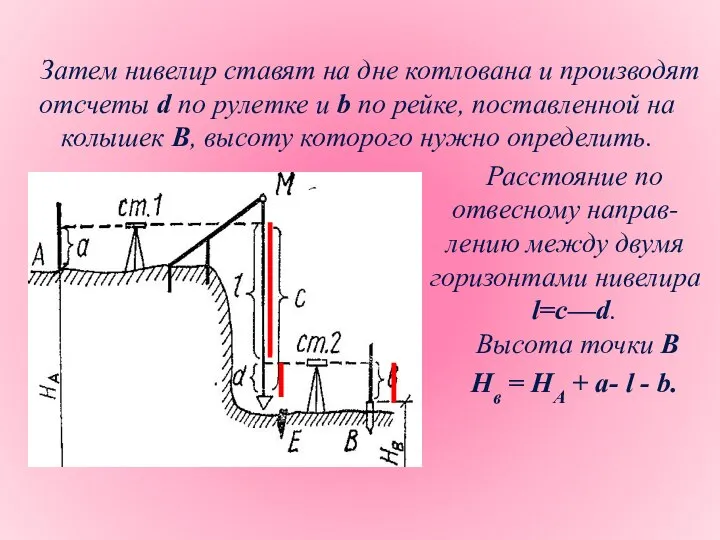
- 20. Затем нивелир ставят на дне котлована и производят отсчеты d по рулетке и b по рейке,
- 21. 3. Способы разбивки основных осей объекта. Главные и основные оси сооружения выносят на местность различными способами:
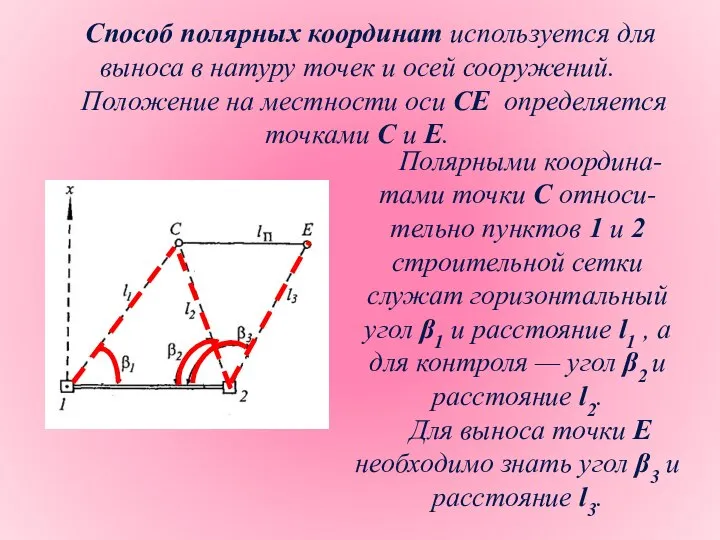
- 22. Способ полярных координат используется для выноса в натуру точек и осей сооружений. Положение на местности оси
- 23. Путем решения обратной геодезической задачи находят дирекционные углы всех направлений, например α12, α1С, α2С, и расстояния
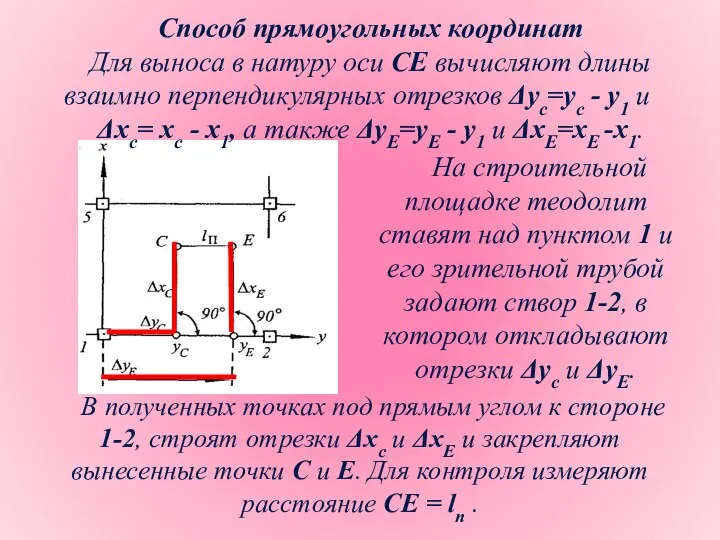
- 24. Способ прямоугольных координат Для выноса в натуру оси СЕ вычисляют длины взаимно перпендикулярных отрезков Δус=ус -
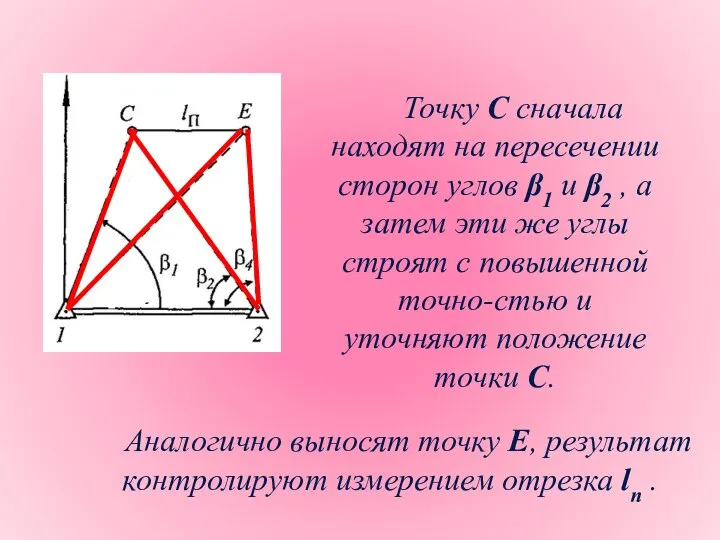
- 25. Способ прямой угловой засечки используется для выноса в натуру точек, находящихся за препятствием (например, водоемом, изрытым
- 26. Точку С сначала находят на пересечении сторон углов β1 и β2 , а затем эти же
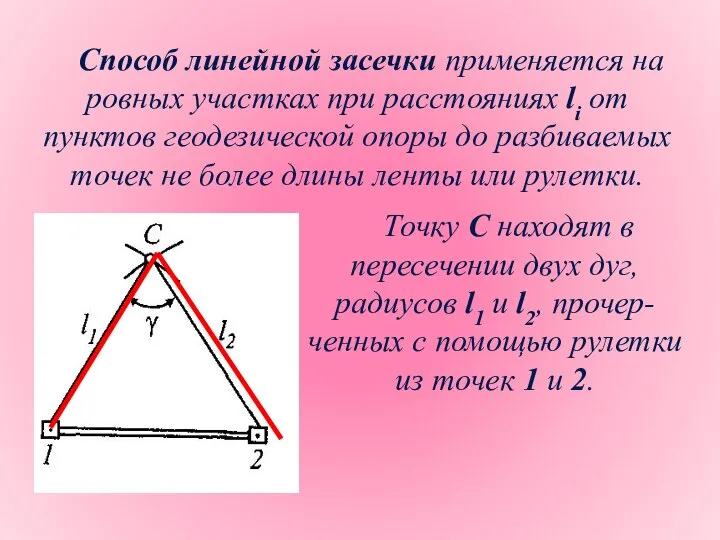
- 27. Способ линейной засечки применяется на ровных участках при расстояниях li от пунктов геодезической опоры до разбиваемых
- 29. Скачать презентацию
















 Водоёмы Вятского края - презентация к уроку Географии_
Водоёмы Вятского края - презентация к уроку Географии_ 6-Мировой океан 1 ДЗ
6-Мировой океан 1 ДЗ Циркуляция атмосферы
Циркуляция атмосферы Вулкан. Что такое вулкан?
Вулкан. Что такое вулкан? Жизнь в арктических поясах и в океане
Жизнь в арктических поясах и в океане 20140222_rybnaya_otrasl_kamchatki
20140222_rybnaya_otrasl_kamchatki Хочу на Сахалин
Хочу на Сахалин Экономическое развитие Камчатского края
Экономическое развитие Камчатского края Лекция№1
Лекция№1 Европейский север
Европейский север Озера, болота, водохранилища
Озера, болота, водохранилища Ямайка мемлекеті
Ямайка мемлекеті Рудные ПИ Таймыр-Североземельской Зоны
Рудные ПИ Таймыр-Североземельской Зоны Формирование рельефа Земли
Формирование рельефа Земли Лаверн
Лаверн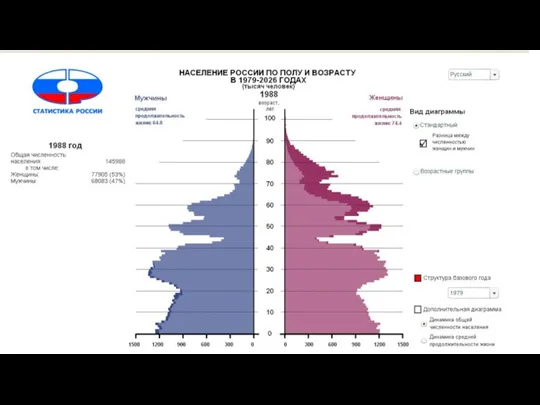 Население России по полу и возрасту
Население России по полу и возрасту Сирия
Сирия Цвети мой край родной (Ко дню Республику и Наадыма)
Цвети мой край родной (Ко дню Республику и Наадыма) 3a6b1ca562c9420687e2cf997d981ec3
3a6b1ca562c9420687e2cf997d981ec3 Великобритания — одно из крупнейших государств Европы
Великобритания — одно из крупнейших государств Европы Презентация на тему Определение географических координат
Презентация на тему Определение географических координат  Презентация на тему Энергетика. Экологические проблемы энергетики
Презентация на тему Энергетика. Экологические проблемы энергетики  Колумбия
Колумбия Яхтинг в Севастополе. Многофункциональная строительная самоподьемная платформа ТЕМП
Яхтинг в Севастополе. Многофункциональная строительная самоподьемная платформа ТЕМП 20140929_evropy
20140929_evropy Многоликая Бразилия
Многоликая Бразилия Приморский район. Виртуальная экскурсия
Приморский район. Виртуальная экскурсия Загадка дыры. Географическое положение
Загадка дыры. Географическое положение